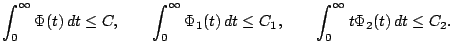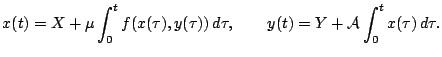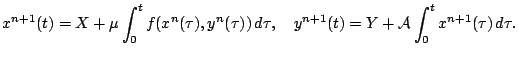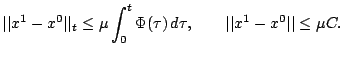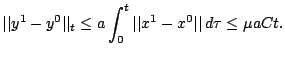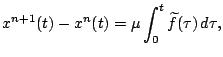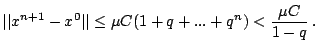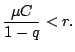<< 1. Введение | Оглавление | 3. Разлет без сближений >>
2. Основная теорема
Слабовозмущенная задача нескольких тел в подходящих переменных может быть представлена системой обыкновенных дифференциальных уравнений следующего вида [19]:
Здесь
Упростим систему (3). Во-первых, примем ![]() за новые
медленные переменные. Этого всегда можно добиться, добавив
за новые
медленные переменные. Этого всегда можно добиться, добавив ![]() к
вектору
к
вектору ![]() и увеличив тем самым порядок системы уравнений. Если же
и увеличив тем самым порядок системы уравнений. Если же
![]() взаимно-однозначно зависит от
взаимно-однозначно зависит от ![]() компонент вектора
компонент вектора ![]() , то
можно не увеличивать числа переменных.
Во-вторых, обратим в нуль вектор
, то
можно не увеличивать числа переменных.
Во-вторых, обратим в нуль вектор ![]() . Тут придется увеличить число
медленных переменных. Для каждого
. Тут придется увеличить число
медленных переменных. Для каждого ![]() , для которого
, для которого ![]() ,
введем новую медленную переменную
,
введем новую медленную переменную ![]() и заменим
и заменим ![]() на
на
![]() :
:
В результате двух преобразований уравнения примут форму
Здесь
где на главной диагонали прямоугольной матрицы
В дальнейшем имеем дело только с системой вида (5).
Функции ![]() считаем непрерывными и удовлетворяющими условию Липшица
в области
считаем непрерывными и удовлетворяющими условию Липшица
в области
![]() ,
к построению которой мы приступаем.
,
к построению которой мы приступаем.
В пространствах
![]() и
и
![]() введем
нормы, которые будем обозначать единым символом
введем
нормы, которые будем обозначать единым символом ![]() , что
не приводит к путанице. Они индуцируют норму в
, что
не приводит к путанице. Они индуцируют норму в
![]() и расстояния в этих трех
пространствах. Для вектор-функций
и расстояния в этих трех
пространствах. Для вектор-функций ![]() ,
,
![]() ,
введем норму
,
введем норму ![]() при фиксированном
при фиксированном ![]() и равномерную норму:
и равномерную норму:
Пусть
![]() - декартово произведение
выпуклых компактов
- декартово произведение
выпуклых компактов
![]() и
и
![]() . Введем виртуальное время
. Введем виртуальное время
![]() . Так как система (5) автономна, за начало
отсчета времени можно взять эпоху
. Так как система (5) автономна, за начало
отсчета времени можно взять эпоху ![]() . Наши построения легче
проводить для полутраекторий, почему мы и ограничились будущим.
Прошлое в автономной системе обладает теми же свойствами, а нужное
впоследствии объединение прошлого и будущего легковыполнимо.
Рассмотрим множество
. Наши построения легче
проводить для полутраекторий, почему мы и ограничились будущим.
Прошлое в автономной системе обладает теми же свойствами, а нужное
впоследствии объединение прошлого и будущего легковыполнимо.
Рассмотрим множество ![]() - декартово произведение множества
непрерывных на
- декартово произведение множества
непрерывных на
![]() функций
функций ![]() со значениями в
со значениями в
![]() и множества постоянных
и множества постоянных
![]() таких, что
таких, что
![]() при каждом
при каждом ![]() . За
. За
![]() примем множество точек из
примем множество точек из
![]() , представимых в виде
, представимых в виде
![]() при
при
![]() и фиксированном
и фиксированном
![]() . Обозначения согласованы:
. Обозначения согласованы: ![]() при
при ![]() .
За
.
За ![]() примем объединение
примем объединение
![]() по всем
по всем
![]() .
.
Согласно леммам 1, 2 (с учетом выпуклости декартова
произведения выпуклых множеств) ![]() и
и ![]() выпуклы и совпадают
с множеством точек, представимых в виде
выпуклы и совпадают
с множеством точек, представимых в виде
![]() при
при
![]() , при фиксированном
, при фиксированном ![]() и при всех
и при всех ![]() соответственно. Это - ключевой момент для дальнейшего. Хотя мы не
знаем поведения траекторий системы (5) как функций реального
времени, мы устанавливаем область, в которой они находятся, исследуя
зависимость фазовых координат как линейных функций виртуального
времени.
соответственно. Это - ключевой момент для дальнейшего. Хотя мы не
знаем поведения траекторий системы (5) как функций реального
времени, мы устанавливаем область, в которой они находятся, исследуя
зависимость фазовых координат как линейных функций виртуального
времени.
В общем случае найдутся начальные данные из ![]() такие, что
отвечающая им полутраектория покинет
такие, что
отвечающая им полутраектория покинет ![]() . Чтобы этого не случилось,
сузим область начальных данных до
. Чтобы этого не случилось,
сузим область начальных данных до
![]() ,
где
,
где ![]() - множество точек из
- множество точек из ![]() , отстоящих от границы
, отстоящих от границы
![]() не менее, чем на
не менее, чем на ![]() ,
, ![]() . По
лемме 3
. По
лемме 3 ![]() - выпуклый компакт. Для непустоты
- выпуклый компакт. Для непустоты ![]() потребуем
потребуем
где
Теперь мы в состоянии сформулировать основную теорему.
Теорема 1. Дана система (5) с непрерывной и удовлетворяющей
условию Липшица в ![]() функцией
функцией ![]() .
Считаем
.
Считаем ![]() функцией виртуального времени
функцией виртуального времени
![]() посредством
посредством

Пусть при каждом ![]() и любом выборе
и любом выборе
![]() , таких,
что
, таких,
что
![]() ,
,
![]() ,
справедливы неравенства
,
справедливы неравенства
причем мажоранты допускают интегральные оценки
Тогда при всех положительных ![]() , подчиненных условию
(6), и
, подчиненных условию
(6), и
1) решения системы (5) с начальными данными из ![]() продолжимы на всю полуось
продолжимы на всю полуось ![]() и не выходят из
и не выходят из ![]() ,
принадлежа
,
принадлежа ![]() при каждом
при каждом ![]() ;
;
2) решения, начинающиеся в ![]() , можно найти, используя
итерации, сходящиеся со скоростью геометрической прогрессии;
сходимость к
, можно найти, используя
итерации, сходящиеся со скоростью геометрической прогрессии;
сходимость к ![]() равномерна относительно начальных данных и времени
на множестве
равномерна относительно начальных данных и времени
на множестве
![]() , сходимость к
, сходимость к ![]() равномерна на множестве
равномерна на множестве
![]() при любом
при любом ![]() ;
;
3) при
![]() переменные
переменные ![]() стремятся к постоянным;
стремятся к постоянным;
4) если предел вектора ![]() отличен от нуля, то вектор
отличен от нуля, то вектор ![]() при
при
![]() стремится к линейной функции времени.
стремится к линейной функции времени.
Поясним смысл четвертого утверждения. Обозначим
Доказательство. Заменим (5) с начальными данными
![]() при
при ![]() равносильной системой интегральных уравнений
равносильной системой интегральных уравнений
Образуем последовательность приближений пикаровского типа. За начальное возьмем интегрируемый случай
Индекс сверху всегда обозначает номер приближения, снизу - номер компоненты.
Нулевое приближение с начальными данными из
![]() с очевидностью не выходит из
с очевидностью не выходит из ![]() .
.
Перейдем к первому приближению.
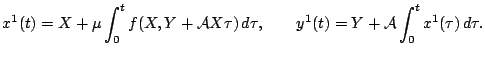
Вследствие (9) имеем
Далее действуем по индукции, предполагая
![]() при
при
![]() .
Согласно (12)
.
Согласно (12)
где
Аналогично (14) имеем
Подставляя (17) в (16), а результат - в (15), получим с учетом (8)
где
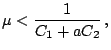
Сложение неравенств (19) позволяет записать
Неравенство (9) влечет
Поэтому при любых
Обозначим через
![]() пределы
пределы
![]() при
при
![]() . Доказательство того, что пределы существуют,
представляют собой решение (5) и справедливы первые два
утверждения теоремы, повторяет доказательство классической теоремы
Пикара-Линделефа [18]. Приведем лишь несколько полезных
формул:
. Доказательство того, что пределы существуют,
представляют собой решение (5) и справедливы первые два
утверждения теоремы, повторяет доказательство классической теоремы
Пикара-Линделефа [18]. Приведем лишь несколько полезных
формул:
Сопоставление (7, 8, 10) показывает, что существует конечный предел
Пусть ![]() . Согласно (10) представим
. Согласно (10) представим ![]() для
достаточно больших
для
достаточно больших ![]() в виде
в виде
![]() ,
где
,
где
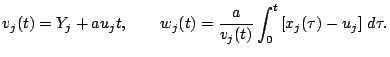
Тогда
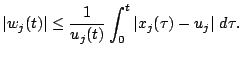
Теорема доказана.
Замечание. Исследуемые в механике уравнения
движения, как правило, инвариантны относительно перемены знака
времени. Система (5) переходит в себя при подстановке
![]() . Поэтому теорема
1 остается справедливой и для прошлого при естественных изменениях
условий. Именно, обозначим области
. Поэтому теорема
1 остается справедливой и для прошлого при естественных изменениях
условий. Именно, обозначим области ![]() через
через
![]() , а аналогичные области, заметаемые полутраекториями при
, а аналогичные области, заметаемые полутраекториями при
![]() , через
, через
![]() . Доказанные свойства
. Доказанные свойства
![]() переносятся и на
переносятся и на
![]() ,
причем
,
причем
![]() . Для справедливости
теоремы 1 при отрицательных
. Для справедливости
теоремы 1 при отрицательных ![]() с очевидными переформулировками
надо лишь заменить (8) на
с очевидными переформулировками
надо лишь заменить (8) на
Обозначим через ![]() объединение
объединение
![]() .
Очевидно,
.
Очевидно,
![]() при
при
![]() при
при
![]() . Утверждение теоремы 1 остается справедливым
с соответствующими переформулировками при
. Утверждение теоремы 1 остается справедливым
с соответствующими переформулировками при
![]() ,
если в (24) заменить пределы интегрирования на
,
если в (24) заменить пределы интегрирования на
![]() .
Заметим только, что бесконечная в обе стороны область
.
Заметим только, что бесконечная в обе стороны область ![]() уже не будет в общем случае выпуклой, что не существенно:
играет роль только выпуклость
уже не будет в общем случае выпуклой, что не существенно:
играет роль только выпуклость ![]() .
.
<< 1. Введение | Оглавление | 3. Разлет без сближений >>
|
Публикации с ключевыми словами:
Небесная механика - задача n-тел - задача трех тел
Публикации со словами: Небесная механика - задача n-тел - задача трех тел | |
См. также:
Все публикации на ту же тему >> | |