Колебания и волны. Лекции.
В.А.Алешкевич, Л.Г.Деденко, В.А.Караваев (Физический факультет МГУ)Издательство Физического факультета МГУ, 2001 г. Содержание
Свободные колебания в диссипативных системах с вязким трением.
В реальных системах всегда происходит диссипация энергии. Если потери энергии не будут компенсироваться за счет внешних устройств, то колебания с течением времени будут затухать и через какое-то время прекратятся вообще.
Формально затухающие колебания описываются уравнением
| (1.46) |
которое, в отличие от (1.2), помимо возвращающей силы ![]() содержит
и силу трения
содержит
и силу трения ![]() Сила сопротивления движению, вообще говоря, зависит
как от направления скорости (например, при сухом трении), так и от величины
скорости (при движении в вязкой среде). Если возвращающая сила
пропорциональна смещению:
Сила сопротивления движению, вообще говоря, зависит
как от направления скорости (например, при сухом трении), так и от величины
скорости (при движении в вязкой среде). Если возвращающая сила
пропорциональна смещению: ![]() где
где ![]() - коэффициент
пропорциональности (для пружинного маятника - жесткость пружины), то
уравнение (1.46) можно переписать в виде
- коэффициент
пропорциональности (для пружинного маятника - жесткость пружины), то
уравнение (1.46) можно переписать в виде
| (1.47) |
где 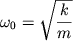 - собственная частота
незатухающих гармонических колебаний.
- собственная частота
незатухающих гармонических колебаний.
Вначале мы рассмотрим затухающие колебания в случае, когда на колеблющееся
тело действует сила вязкого трения, пропорциональная скорости: ![]() Такая ситуация может иметь место, например, при
колебательном движении тела в воздухе или жидкости, когда число Рейнольдса
Такая ситуация может иметь место, например, при
колебательном движении тела в воздухе или жидкости, когда число Рейнольдса
![]() или
или ![]() . Тогда уравнение (1.47) можно записать в виде:
. Тогда уравнение (1.47) можно записать в виде:
| (1.48) |
где ![]() - коэффициент, или показатель затухания.
- коэффициент, или показатель затухания.
Общая идея решения однородных линейных уравнений типа (1.48) заключается в
следующем: в качестве функциональной зависимости ![]() надо выбрать такую,
которая при дифференцировании по времени переходит в саму себя, то есть
экспоненту:
надо выбрать такую,
которая при дифференцировании по времени переходит в саму себя, то есть
экспоненту: ![]() Подставим ее в уравнение (1.48):
Подставим ее в уравнение (1.48):
| (1.49) |
Поскольку ![]() получаем так называемое
"характеристическое" уравнение:
получаем так называемое
"характеристическое" уравнение:
| (1.50) |
которое в данном случае (для уравнения второго порядка) имеет два корня
| (1.51) |
а само уравнение (1.48) - два независимых решения: ![]() и
и ![]() В силу
линейности уравнения (1.48) сумма любых его решений также является решением,
то есть справедлив так называемый "принцип суперпозиции" решений, и общим
решением данного уравнения является
В силу
линейности уравнения (1.48) сумма любых его решений также является решением,
то есть справедлив так называемый "принцип суперпозиции" решений, и общим
решением данного уравнения является
| (1.52) |
Решение содержит две независимые константы ![]() и
и ![]() которые
определяются из начальных условий
которые
определяются из начальных условий ![]()
В зависимости от соотношения ![]() и
и ![]() возможны три случая.
возможны три случая.
Если ![]() то
то ![]() где
где ![]() -
"мнимая" единица. Решение является комплексным1, но, поскольку начальные условия
действительные, то с помощью формулы Эйлера:
-
"мнимая" единица. Решение является комплексным1, но, поскольку начальные условия
действительные, то с помощью формулы Эйлера:
| (1.53) |
нетрудно показать, что общее решение будет действительно и может быть записано в виде:
| (1.54) |
то есть представляет собой затухающие колебания, частота которых ![]() меньше, чем у собственных незатухающих колебаний:
меньше, чем у собственных незатухающих колебаний:
| (1.55) |
Колебания, описываемые (1.54), не являются гармоническими (рис. 1.14). Под их амплитудой будем понимать величину
| (1.56) |
которая монотонно убывает со временем. "Длительность" колебаний характеризуется временем затухания
| (1.57) |
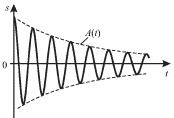 |
| Рис. 1.14. |
Если подставить ![]() в (1.56), то легко видеть, что по истечении времени
затухания
в (1.56), то легко видеть, что по истечении времени
затухания ![]() амплитуда убывает в е раз. Количество совершенных системой
колебаний за время
амплитуда убывает в е раз. Количество совершенных системой
колебаний за время ![]() равно отношению этого времени к периоду
затухающих колебаний
равно отношению этого времени к периоду
затухающих колебаний ![]() Если затухание в системе мало
Если затухание в системе мало
![]() то период колебаний
то период колебаний ![]() и число этих колебаний велико:
и число этих колебаний велико:
| (1.58) |
Экспоненциальный закон убывания амплитуды со временем позволяет ввести
безразмерный параметр - логарифмический декремент затухания ![]() который равен логарифму отношения двух последовательных отклонений в одну и
ту же сторону:
который равен логарифму отношения двух последовательных отклонений в одну и
ту же сторону:
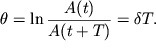 | (1.59) |
Из (1.57), (1.58) и (1.59) находим:
| (1.60) |
Логарифмический декремент затухания можно оценить, если подсчитать число
колебаний, совершенных системой за время затухания ![]() то есть до
уменьшения амплитуды колебаний примерно в 3 раза. Чем больше число этих
колебаний, тем меньше потери энергии в системе.
то есть до
уменьшения амплитуды колебаний примерно в 3 раза. Чем больше число этих
колебаний, тем меньше потери энергии в системе.
Проследим за убыванием энергии, запасенной осциллятором, с течением времени. Используя (1.54), запишем по аналогии с (1.24) и (1.25) выражения для потенциальной и кинетической энергий осциллятора:
| (1.61) |
| (1.62) |
Заметим, что, строго говоря, скорость равна
| (1.63) |
Очевидно, что если ![]() то первым слагаемым в (1.63) можно
пренебречь и записать выражение для кинетической энергии в виде (1.62).
Суммарная энергия осциллятора убывает со временем:
то первым слагаемым в (1.63) можно
пренебречь и записать выражение для кинетической энергии в виде (1.62).
Суммарная энергия осциллятора убывает со временем:
| (1.64) |
Примем во внимание, что при ![]() частота
частота ![]() Так как
Так как ![]() то (1.64)
окончательно запишется в виде
то (1.64)
окончательно запишется в виде
| (1.65) |
Полная энергия осциллятора, равная вначале ![]() монотонно убывает со временем по экспоненциальному
закону и уменьшается в е раз за время
монотонно убывает со временем по экспоненциальному
закону и уменьшается в е раз за время
| (1.66) |
"Качество" колебательной системы характеризуют безразмерным параметром ![]() называемым добротностью. Добротность пропорциональна отношению запасенной
энергии
называемым добротностью. Добротность пропорциональна отношению запасенной
энергии ![]() к энергии
к энергии ![]() теряемой за период (рис. 1.15):
теряемой за период (рис. 1.15):
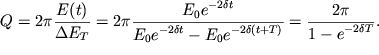 | (1.67) |
Если число колебаний велико, то ![]() Тогда
Тогда
| (1.68) |
При экспоненциальном законе убывания энергии со временем добротность ![]() оказывается постоянной величиной, которую, как и логарифмический декремент
затухания
оказывается постоянной величиной, которую, как и логарифмический декремент
затухания ![]() можно легко оценить по числу колебаний
можно легко оценить по числу колебаний ![]() совершенных системой до их полного прекращения (за время
совершенных системой до их полного прекращения (за время ![]() амплитуда колебаний уменьшается в
амплитуда колебаний уменьшается в ![]() раз, то есть
колебания практически полностью затухают).
раз, то есть
колебания практически полностью затухают).
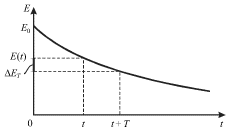 |
| Рис. 1.15. |
Следует отметить, что добротность не только характеризует затухание колебаний, но и является важной величиной, определяющей параметры вынужденных колебаний, осуществляемых под действием внешней периодической силы (см. далее).
1Более подробно метод комплексных амплитуд будет обсуждаться ниже, при рассмотрении вынужденных колебаний.|
Публикации с ключевыми словами:
колебания - волны
Публикации со словами: колебания - волны | |
|
См. также:
| |