Астронет > Колебания и волны

по текстам по ключевым словам в глоссарии по сайтам перевод по каталогу

Колебания и волны. Лекции.

В.А.Алешкевич, Л.Г.Деденко, В.А.Караваев (Физический факультет МГУ)
Издательство Физического факультета МГУ, 2001 г. Содержание

Негармонические колебания математического маятника.

Колебания математического маятника при больших амплитудах, как уже отмечалось, не будут гармоническими. Это происходит потому, что возвращающая сила в правой части уравнения (1.28) пропорциональна $\sin \alpha$ и при больших $\alpha$ становится меньше той "линейной" силы (пропорциональной $\alpha$ ), которая возвращает колеблющуюся массу в положение равновесия за неизменное время, равное четверти периода колебаний. Такая "линейная" сила обеспечивает независимость этого времени от амплитуды $\alpha _{0},$ т.е. изохронность колебаний.

Для анализа колебаний при больших амплитудах $\alpha _{0}$ запишем разложение $\sin \alpha$ в ряд:

$\sin \alpha = \alpha - {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 6}}}\alpha ^{3} + \ldots \quad,$

(1.35)

в котором отброшены члены более высокого порядка: $\alpha ^{5}, \alpha ^{7}$ и т.д. Подстановка (1.35) в (1.28) приводит к нелинейному уравнению колебаний:

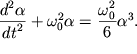${\displaystyle \frac{\displaystyle {\displaystyle d^{2}\alpha }}{\displaystyle {\displaystyle dt^{2}}}} + \omega _{0}^{2} \alpha = {\displaystyle \frac{\displaystyle {\displaystyle \omega _{0}^{2} }}{\displaystyle {\displaystyle 6}}}\alpha ^{3}.$

(1.36)

Решением этого уравнения уже не будет гармоническая функция. Действительно, допустим, что решением уравнения (1.36) будет гармоническое колебание вида $\alpha (t) = \alpha _{0} \sin (\omega t + \varphi _{0} ).$ Подставляя это выражение в правую часть (1.36) и учитывая тригонометрическое тождество

$\sin ^{3}\omega t \equiv {\displaystyle \frac{\displaystyle {\displaystyle 3}}{\displaystyle {\displaystyle 4}}}\sin \omega t - {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 4}}}\sin 3\omega t,$

(1.37)

приходим к противоречию. Получается так, что нелинейный член в правой части уравнения изменяется во времени не только с основной частотой $\omega,$ но также и с утроенной частотой $3\omega$ (частотой третьей гармоники). Чтобы устранить это противоречие, будем считать, что колебания маятника происходят одновременно на частотах $\omega$ и $3\omega$ так, что

$\alpha (t) = \alpha _{0} \sin (\omega t + \varphi _{0} ) + \varepsilon \alpha _{0} \sin 3(\omega t + \varphi _{0} ),$

(1.38)

где $\varepsilon$ - безразмерный параметр.

Подставляя (1.38) в (1.36), снова обнаруживаем, что нелинейный член, помимо двух частот $\omega$ и $3\omega,$ меняется во времени и на частоте $9\omega .$ Это говорит о том, что решение (1.38) не является полным (в нем отсутствуют высшие гармоники $9\omega, 27\omega$ и т.д.). Между тем, если амплитуда колебаний $\alpha _{0}$ не очень велика, то параметр $\varepsilon \ll 1,$ и отсутствующие члены с высшими гармониками имеют амплитуды $\varepsilon ^{2}\alpha _{0}, \varepsilon ^{3}\alpha _{0}$ и т. д., которые много меньше амплитуды третьей гармоники $\varepsilon \alpha _{0} .$

Теперь рассчитаем частоту $\omega .$ Для простоты положим $\varphi _{0} = 0$ (маятник получает начальный толчок в положении равновесия). Используя (1.38), запишем каждый из трех членов уравнения (1.36), опуская слагаемые, имеющие порядок малости $\varepsilon ^{2}$ и выше:

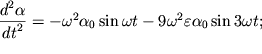${\displaystyle \frac{\displaystyle {\displaystyle d^{2}\alpha }}{\displaystyle {\displaystyle dt^{2}}}} = - \omega ^{2}\alpha _{0} \sin \omega t - 9\omega ^{2}\varepsilon \alpha _{0} \sin 3\omega t;$	(1.39)
$\omega _{0}^{2} \alpha = \omega _{0}^{2} \alpha _{0} \sin \omega t + \omega _{0}^{2} \varepsilon \alpha _{0} \sin 3\omega t;$
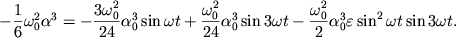$- {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 6}}}\omega _{0}^{2} \alpha ^{3} = - {\displaystyle \frac{\displaystyle {\displaystyle 3\omega _{0}^{2} }}{\displaystyle {\displaystyle 24}}}\alpha _{0}^{3} \sin \omega t + {\displaystyle \frac{\displaystyle {\displaystyle \omega _{0}^{2} }}{\displaystyle {\displaystyle 24}}}\alpha _{0}^{3} \sin 3\omega t - {\displaystyle \frac{\displaystyle {\displaystyle \omega _{0}^{2} }}{\displaystyle {\displaystyle 2}}}\alpha _{0}^{3} \varepsilon \sin ^{2}\omega t\sin 3\omega t.$

Заметим, что в последнем равенстве третье слагаемое в правой части, содержащее множитель $\alpha _{0}^{3} \varepsilon,$ мало по сравнению с двумя предыдущими, и его также можно отбросить.

Сложим полученные три равенства. В силу (1.36), сумма левых частей равенств (1.39) равна нулю. Поэтому

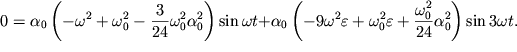$0 = \alpha _{0} \left( {\displaystyle - \omega ^{2} + \omega _{0}^{2} - {\displaystyle \frac{\displaystyle {\displaystyle 3}}{\displaystyle {\displaystyle 24}}}\omega _{0}^{2} \alpha _{0}^{2} } \right)\sin \omega t + \alpha _{0} \left( {\displaystyle - 9\omega ^{2}\varepsilon + \omega _{0}^{2} \varepsilon + {\displaystyle \frac{\displaystyle {\displaystyle \omega _{0}^{2} }}{\displaystyle {\displaystyle 24}}}\alpha _{0}^{2} } \right)\sin 3\omega t.$

(1.40)

Поскольку равенство (1.40) должно выполняться для любого момента времени, то каждое из выражений, стоящих в круглых скобках, должно равняться нулю. Из равенства нулю первого выражения легко определить квадрат частоты основной гармоники

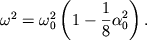$\omega ^{2} = \omega _{0}^{2} \left( {\displaystyle 1 - {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 8}}}\alpha _{0}^{2} } \right).$

(1.41)

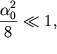Если ${\displaystyle \frac{\displaystyle {\displaystyle \alpha _{0}^{2} }}{\displaystyle {\displaystyle 8}}} \ll 1,$ то для частоты получим

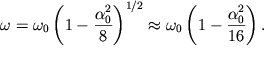$\omega = \omega _{0} \left( {\displaystyle 1 - {\displaystyle \frac{\displaystyle {\displaystyle \alpha _{0}^{2} }}{\displaystyle {\displaystyle 8}}}} \right)^{1 / 2} \approx \omega _{0} \left( {\displaystyle 1 - {\displaystyle \frac{\displaystyle {\displaystyle \alpha _{0}^{2} }}{\displaystyle {\displaystyle 16}}}} \right).$

(1.42)

Последнее выражение показывает, что с возрастанием амплитуды колебаний их частота уменьшается (период увеличивается), т.е. нарушается изохронность колебаний.

Приравняем далее нулю второе выражение в круглых скобках в формуле (1.40):

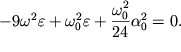$- 9\omega ^{2}\varepsilon + \omega _{0}^{2} \varepsilon + {\displaystyle \frac{\displaystyle {\displaystyle \omega _{0}^{2} }}{\displaystyle {\displaystyle 24}}}\alpha _{0}^{2} = 0.$

(1.43)

Считая, что $\omega \approx \omega _{0},$ находим величину малого коэффициента $\varepsilon$ :

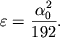$\varepsilon = {\displaystyle \frac{\displaystyle {\displaystyle \alpha _{0}^{2} }}{\displaystyle {\displaystyle 192}}}.$

(1.44)

Если положить $\alpha _{0} = 15^{\circ} = 0,26 рад,$ то $\varepsilon = 3,5 \cdot 10^{ - 4},$ и вклад третьей гармоники в колебания ничтожно мал. Отличие частоты \omega от частоты гармонических колебаний $\omega _{0}$ составит величину

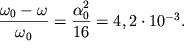${\displaystyle \frac{\displaystyle {\displaystyle \omega _{0} - \omega }}{\displaystyle {\displaystyle \omega _{0} }}} = {\displaystyle \frac{\displaystyle {\displaystyle \alpha _{0}^{2} }}{\displaystyle {\displaystyle 16}}} = 4,2 \cdot 10^{ - 3}.$

(1.45)

Даже при $\alpha _{0} \sim 1 рад \; \varepsilon \approx 5 \cdot 10^{ - 3},$ а ${\displaystyle \frac{\displaystyle {\displaystyle \omega _{0} - \omega }}{\displaystyle {\displaystyle \omega _{0} }}}\sim 6\% .$ Таким образом, приближенным решением уравнения (1.36) будет (1.38), где частота $\omega$ определяется (1.41), а параметр $\varepsilon$ находится из (1.44).

Заметим, что негармонические колебания могут возникать не только при больших отклонениях от положения равновесия системы. Например, если в разложении возвращающей силы $F_{\tau } (s)$ по степеням $s$ отсутствует линейный член, и оно начинается с члена, пропорционального $s^{3},$ то колебания будут ангармоническими при любых, даже сколь угодно малых отклонениях.

Назад| Вперед

Публикации с ключевыми словами: колебания - волны Публикации со словами: колебания - волны
См. также: Эхо из глубин красного гиганта

Обсудить эту публикацию

Версия для печати

Астрометрия - Астрономические инструменты - Астрономическое образование - Астрофизика - История астрономии - Космонавтика, исследование космоса - Любительская астрономия - Планеты и Солнечная система - Солнце