Астронет > Обычные и необычные фазовые переходы

по текстам по ключевым словам в глоссарии по сайтам перевод по каталогу

Обсуждается классификация фазовых переходов и поведение систем, совершающих фазовые переходы первого и второго рода. Рассмотрено отрывание адсорбированной полимерной цепи от плоскости под действием постоянной внешней силы. Показано, что в этом случае имеет место необычный фазовый переход, имеющий черты переходов первого и второго рода одновременно.

Модель "липкой ленты"

Полимерные цепи в растворе представляют собой длинные нити, хаотически свернутые в пространстве и постоянно меняющие свою форму и размеры под действием тепловых беспорядочных ударов молекул растворителя. Получить представление о свойствах полимерных цепей в растворе можно, прочитав популярные книги [Гросберг А.Ю., Хохлов А.Р.,1989],[Элиас Г.Г.,1990]. Рассмотрим полимерную молекулу, плавающую в растворе вблизи некоторой плоской поверхности. Закрепим один конец полимерной цепи на плоскости, а второй оставим свободным. Тогда полимерная цепь будет напоминать длинную водоросль, растущую на дне пруда (рис. 5). Если дно пруда липкое, то такая водоросль скоро окажется скрепленной с поверхностью дна различными своими участками. Аналогичным образом ведет себя полимерная цепь вблизи адсорбирующей (липкой) поверхности. При большой энергии адсорбции почти все участки цепи будут лежать на поверхности. В этом состоянии полимерную цепь можно представить как длинную липкую ленту (рис. 5).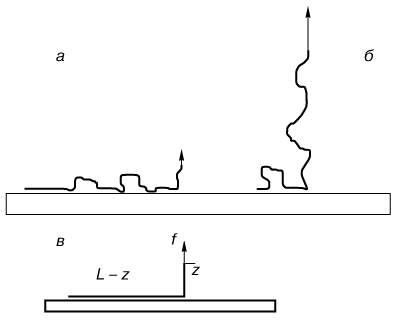

Изображение полимерной цепи, адсорбированной на плоскости при небольшой отрывающей силе (a) и почти полностью оторванной от плоскости при большой силе (б). Модель

Рис. 5. Изображение полимерной цепи, адсорбированной на плоскости при небольшой отрывающей силе (a) и почти полностью оторванной от плоскости при большой силе (б). Модель "липкой ленты" (в).

Приложим теперь к свободному концу полимерной цепи постоянную силу f, направленную перпендикулярно плоскости и отрывающую цепь от плоскости. Контурную длину макромолекулы обозначим через L, а через q обозначим силу адсорбции, с которой удерживается на плоскости участок цепи единичной длины. Если свободный конец цепи находится на высоте z, то потенциальная энергия оторванной части равна fz. Остальная часть цепи длиной $L-z$ адсорбирована на плоскости, имея энергию $q(L-z)$ . При отрывании полимерной цепи затрачивается работа по преодолению энергии адсорбции, но выигрывается потенциальная энергия, связанная с подъемом конца цепи над плоскостью. Очевидно, отрывание произойдет при $f=q$ , когда отрывающая сила сравняется с адсорбционной силой. Вероятность нахождения свободного конца цепи на высоте z имеет вид

$P(z)\sim \exp{[fz+q(l-z)]}\sim \exp (tz/l).$

(2)

где $t = (f - q)L$ .
Рассмотрим степень вытянутости конца полимерной цепи над плоскостью $S=z/L$ . На рисунке 6 показана зависимость средней степени вытянутости от величины $f-q$ . Будем считать, что липкость поверхности, то есть величина q, постоянна. Как видно из рисунка 6, по мере возрастания отрывающей силы высота конца полимерной молекулы увеличивается. Чем длиннее макромолекула, тем более резко происходит переход цепи из адсорбированного в оторванное состояние. В пределе бесконечно длинной полимерной цепи величина <S>, а следовательно, и энергия макромолекулы изменятся скачком при $f = q$ . Как уже говорилось в разделе Классификация фазовых переходов, такое скачкообразное изменение энергии системы является характерным признаком фазовых переходов первого рода.

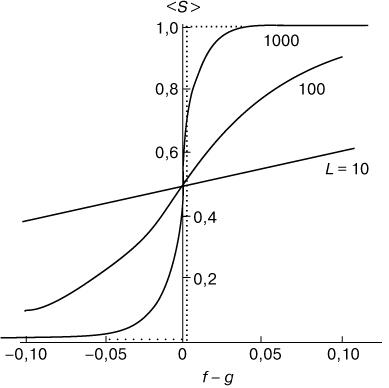Зависимость степени вытянутости полимерных цепей различной длины от разности отрывающей силы и силы адсорбции в модели

Рис. 6. Зависимость степени вытянутости <S> с полимерных цепей различной длины L от разности $f - g$ отрывающей силы и силы адсорбции в модели "липкой ленты". Поведение асимптотически длинной цепи показано пунктиром.

Посмотрим, как проявляется фазовый переход в полимерной цепи, содержащей небольшое число звеньев, то есть в "малой системе". Зафиксируем величину $f - q$ , то есть удаленность от точки фазового перехода, и рассмотрим поведение параметра <S> в зависимости от длины макромолекулы (рис. 7). Уменьшению $L-1$ отвечает переход от малой системы (короткой цепи) к большой системе (длинной цепи). Бесконечно длинная цепь при $f - q > 0$ находится в оторванном состоянии, имея максимальную вытянутость, равную единице. При $f - q < 0$ длинная полимерная цепь выложена на плоскости и имеет нулевую вытянутость. В то же время вытянутость коротких цепей вблизи точки фазового перехода - при $f - q$ , близких к нулю, - всегда близка к 1/2 независимо от знака $f - q$ . Можно сказать, что, находясь вблизи точки перехода, короткая полимерная цепь "не знает", к какой фазе она принадлежит, и в области перехода оба состояния для нее одинаково вероятны.

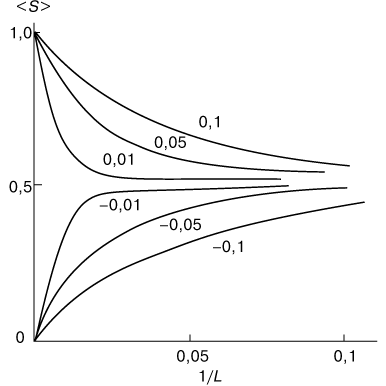Зависимость степени вытянутости макромолекулы от ее обратной длины при различном удалении от точки фазового перехода в модели

Рис. 7. Зависимость степени вытянутости макромолекулы <S> от ее обратной длины 1/L при различном удалении от точки фазового перехода $f = g$ в модели "липкой ленты".

Естественно ввести характерную длину макромолекулы L^*, при достижении которой цепь можно начинать считать "длинной", определив L^* соотношением

$L^*\approx ||f-q||^-1$ .

(3)

Такая характерная длина в действительности представляет собой некоторую область, а не какое-то точное значение. В длинных полимерных молекулах с $L\gg L^*$ (в "больших" системах) свойства резко меняются с изменением $f - g$ в окрестности перехода. Степень вытянутости и энергия таких молекул пропорциональны 1/L, и их наклон определяется знаком величины $f - q$ . С другой стороны, свойства коротких цепей, то есть "малых" систем, слабо зависят от управляющего параметра $f - q$ . Вдали от точки фазового перехода величина L^* мала и даже не очень длинную полимерную цепь можно рассматривать как термодинамически обычную, "большую" систему. Вблизи точки перехода L^* становится очень большой величиной и только очень длинная полимерная цепь будет обладать характеристиками определенной фазы, в то время как менее длинные молекулы будут представлять собой "малые" системы. В низкомолекулярных системах число элементов обычно столь велико (порядка числа Авогадро), что эти системы всегда можно считать асимптотически большими. Влияние размеров системы на ее свойства в окрестностях фазового перехода рассматривают только при моделировании таких систем на компьютерах. При этом, чтобы получить предельные асимптотические значения величин, проводят экстраполяцию результатов по 1/L. Как видно из рисунка 7, такие экстраполяции имеют смысл только для "больших" систем. Пользуясь формулой (2), можно вычислить любые характеристики отрываемой цепи и, в частности, ее теплоемкость. Оказывается, что для бесконечно длинной адсорбированной цепи, отрываемой от плоскости постоянной силой, имеется резкий всплеск теплоемкости в точке $f = q$ , что также характерно для фазовых переходов первого рода.

Отсутствие бимодальности у функции распределения

Поведение энергии и теплоемкости при отрывании полимерной цепи от липкой плоскости постоянной силой вполне согласуется с общепринятыми представлениями о фазовом переходе первого рода в этой системе. Однако, как мы увидим ниже, в рассматриваемой системе имеется ряд черт, свойственных фазовым переходам второго рода. Обратимся к распределению свободного конца цепи по высоте - формула (2). Поскольку потенциальная энергия пропорциональна высоте конца $S = z / L$ , то функция распределения по энергии $P(S)\sim\exp(tS)$ имеет тот же вид, что и распределение по высоте, и не является бимодальной ни при каких значениях внешних параметров; она всегда или экспоненциально убывает, или экспоненциально возрастает, а в самой точке перехода представляет собой константу. Соответственно при отрывании "липкой ленты" всегда существует только одно равновесное значение высоты конца, а следовательно, и средней энергии системы. Естественно, что при этом никаких метастабильных состояний системы нет в принципе, что характерно для фазовых переходов второго рода. Мы рассматривали отрывание адсорбированной макромолекулы, используя простую модель "липкой ленты", однако оказывается, что и гораздо более детальное описание приводит к тем же результатам. Интересно понять, почему отрываемая от поверхности полимерная цепь совершает необычный фазовый переход, отличный от фазовых переходов в низкомолекулярных системах. Для этого возвратимся к началу статьи и вспомним, что говорилось о границе раздела между фазами и о появлении зародышей новой фазы при переходах первого рода. При появлении новой фазы надо отграничить ее от другой фазы. Создание такой границы энергетически невыгодно и требует преодоления некоторого потенциального барьера. Именно из-за наличия такого барьера становятся возможными перегретые и переохлажденные метастабильные состояния жидкости и пара. В полимерной цепи есть два различных состояния - адсорбированное и оторванное. Границей между этими состояниями (фазами) является всего одно звено. Фактически в этой системе нет потерь на создание границы, а значит, нет и барьера, затрудняющего появление новой фазы. Раз нет барьера, то нет и метастабильных состояний, нет бимодальности функций распределения.

Заключение

Итак, при отрывании адсорбированной полимерной молекулы имеет место необычный фазовый переход. Этот переход, с одной стороны, обладает чертами, характерными для фазовых переходов первого рода: скачок энергии, всплеск флуктуаций и выделение скрытой теплоты. С другой стороны, в поведении рассматриваемой системы проявляются черты фазового перехода второго рода: полное отсутствие метастабильных состояний и отсутствие бимодальности у функции распределения по энергии. Необычность фазового перехода при отрывании адсорбированной полимерной молекулы связана с необычностью границы, существующей между ее состояниями (фазами). Эта граница четко определена и наглядна, но столь узка, что энергетические потери на ее создание пренебрежимо малы. Замечательным свойством рассматриваемой полимерной системы является возможность получить строгое аналитическое описание обеих фаз в рамках единого рассмотрения с позиций статистической физики. Более того, оказывается возможным проследить аналитически, как по мере увеличения числа частиц в системе формируются скачки, характерные для фазовых переходов первого рода. Для классических низкомолекулярных систем, совершающих фазовые переходы первого рода, единообразное описание обеих фаз достигается только в результате численных расчетов на компьютерах, а исследование эффектов, связанных с конечностью системы, представляет сложнейшую задачу и требует изощренных методов. Решение задачи об отрывании адсорбирующейся макромолекулы закладывает основу для построения теории адгезионной прочности полимеров на границе раздела фаз.

Литература

Штейнберг А.С. Репортаж из мира сплавов. Библиотечка "Квант". М.: Наука, 1989.
Волькенштейн М.В. Физика и биология. М.: Наука, 1980.
Эткинс П. Физическая химия. Т. 1. Гл. 7. М.: Мир. 1980.
Ландау Л.Д., Лифшиц Е.М. Статистическая физика. Часть 1. М.: Наука, 1976.
Гросберг А.Ю., Хохлов А.Р. Физика в мире полимеров. Библиотечка "Квант". М.: Наука, 1989.
Элиас Г.Г. Мегамолекулы. Л.: Химия, 1990.

Публикации с ключевыми словами: фазовые переход второго рода - фазовые переход первого рода - фазовый переход Публикации со словами: фазовые переход второго рода - фазовые переход первого рода - фазовый переход
См. также: Дальний и ближний порядок Введение в физику открытых систем Обычные и необычные фазовые переходы Агрегатные состояния

Мнение читателя [1]

Версия для печати

Астрометрия - Астрономические инструменты - Астрономическое образование - Астрофизика - История астрономии - Космонавтика, исследование космоса - Любительская астрономия - Планеты и Солнечная система - Солнце