Дальний и ближний порядок - наличие пространственной корреляции микроструктуры вещества либо в пределах всего макроскопического образца (дальний порядок), либо в области с конечным радиусом корреляции (6лижнй порядок). Состояние вещества, характеризуемое наличием дальнего порядка, называют упорядоченной фазой, а состояние, в котором дальний порядок отсутствует, - неупорядоченной фазой. Фазовый переход из неупорядоченной фазы в упорядоченную может быть переходом первого или второго рода. Если упорядочение происходит в результате фазового перехода второго рода, то в неупорядоченной фазе есть ближний порядок, причем при приближении к точке перехода корреляционный радиус .

Различаются следующие виды упорядочения: координационное (в расположении частиц вещества); ориентационное (в ориентации частиц); магнитное (упорядочение в ориентации магнитных моментов).

Координационное упорядочение

В жидкости вероятность пребывания атома в точке с пространственной координатой r или ее удельная плотностъ в среднем одинаковы, т. е. средняя удельная плотность не зависит от . Однако в жидкости существуют корреляции в расположении соседних атомов. Корреляционная функция, описывающая отклонения от () в разных точках жидкости:

,

(10)

отлична от нуля при r - r' < R_c. Т. о., атомы жидкости на расстояниях, меньших R_c, образуют ближний координационный порядок. Отклонение от называют параметром порядка.

При кристаллизации возникает периодическая пространственная модуляция , т. к. атомы в кристаллах занимают положения, отвечающие узлам кристаллической решётки. В результате отклонение плотности от средней становится периодической функцией координат. Это означает, что в кристаллах имеет место дальний координационный порядок.

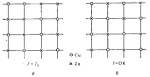
Друюй пример координационного упорядочения дают сплавы. Например, сплав, содержащий равные количества Cu и Zn, имеет простую кубическую решетку. При высоких температурах в результате диффузии её узлы заняты с равной вероятностно атомами Cu или Zn (рис. а) и средняя удельная плотность атомов Cu однородна, т. е. не зависит от координат узла (неупорядоченная фаза). При понижении температуры атомы Cu и Zn образуют правильное расположение (упорядоченная фаза, рис. б).

Если ввести параметр порядка , то при высокой температуре , а при низкой температуре

.

(2)

Переход из неупорядоченной фазы в упорядоченную в сплавах часто происходит в результате фазового перехода второго рода. При этом упорядочение происходит постепенно, т. е. параметр порядка для температур T>T_c (T_c - температура фазового перехода), а при T<T_c постепенно возрастает с понижением температуры. При T>T_c дальнего порядка нет, но ближний порядок есть. Это означает, что, хотя для двух узлов, удаленных друг от друга на расстояния R>R_c, вероятности занять их атомами Cu одинаковы, на расстояниях R<R_c эти вероятности коррелируют друг с другом, как в упорядоченной фазе. При при6лижении к T_c радиус корреляции и ближний порядок превращается в дальний.

И в кристаллах, и в сплавах высокотемпературная фаза является неупорядоченной. Такая ситуация, как правило, типична для всех видов упорядочения. При повышении температуры разупорядочивающее тепловое движение становится более интенсивным, что приводит при достаточно высоких температурах к разрушению корреляций, т. е. к отсутствию дальнего порядка и ослаблению ближнего порядка (к уменьшению R_c).

Ориентационное и магнитное упорядочения

В изотропной жидкости, состоящей из анизотропных, но случайно ориентированных молекул, может происходить фазовый переход в анизотропную жидкость, в которой молекулы имеют преимущественную ориентацию (см. Жидкие кристаллы). Параметром порядка при таком ориентационном упорядочении является спонтанная поляризация или константа анизотропии диэлектрической проницаемости равные нулю в изотропной жидкости и отличные от нуля в жидком кристалле.

Магнитное упорядочение состоит в том, что магнитные моменты атомов, ориентированные при высокой температуре в разных точках независимо (парамагнетик), при понижении температуры ниже точек Кюри или Нееля упорядочиваются и либо имеют одинаковое направление и ориентацию (ферромагнетик), либо одинаковое направление, но разные ориентации. В последнем случае они образуют магнитные подрешётки, причём ориентации магнитных моментов для атомов каждой подрешетки одинаковы, а для атомов разных подрешёток - противоположны (антиферромагнетик). Параметром порядка в ферромагнетиках является намагниченность.

Упорядочение в квантовых жидкостях

Все перечисленные виды упорядочения имели в качестве параметра порядка классические величины. Имеется важная группа упорядочивающихся систем, в которых параметром порядка является макроскопическая волновая функция всего о6разца. Такое квантовое упорядочение есть в сверхтекучем состоянии изотопов гелия He^II, ³He-A, ³He-B (см. Гелий жидкий, Сверхтекучесть) и в сверхпроводящей фазе металлов (см. Сверхпроводимость). В этих случаях при температуре T выше температуры фазового перехода волновые функции всех частиц, относящиеся к удалённым друг от друга точкам пространства, скоррелированы. Упорядоченное состояние характеризуется скоррелированной фазой волновых функций частиц, которая может измениться во всем образце в целом, но не может измениться независимо в разных точках.

Изменение симметрии при упорядочении

В классификации упорядоченных и неупорядоченных фаз важную роль играет симметрия. Например, в случае сплава в высокотемпературной фазе все узлы решётки эквивалентны, поэтому здесь имеет место инвариантность относительно трансляции на любое число периодов кристаллической решётки, т. е. непрерывная симметрия. В упорядоченной фазе сплава эквивалентны только узлы, занятые, например, атомами Cu. Ей отвечает инвариантность относительно таких трансляций, которые переводят один из узлов, занятых атомом Cu, в другой (дискретная симметрия). Т. о., упорядоченной фазе отвечает более низкая симметрия.

В момент фазового перехода симметрия меняется скачком. Однако параметр порядка, который является количественной мерой нарушения симметрии, может возникать как скачком, так и непрерывно. Математической теорией, классифицирующей симметрии различных фаз, является теория групп. Изучение симметрии упорядоченной и неупорядоченной фаз позволяет, в частности, выяснить тип фазового перехода.

Если при упорядочении нарушается непрерывная симметрия, то говорят, что упорядоченная фаза обладает дополнительной по сравнению с неупорядоченной фазой "жесткостью". Это означает, что малая деформация требует дополнительной затраты энергии. Например, при переходе жидкости в кристаллическое состояние нарушается инвариантность относительно трансляции частиц на произвольный вектор . Следствием этого является появление в твёрдом теле дополнительной жесткости по отношению к деформации сдвига, которая отсутствует в жидкости. В He^II при согласованных изменениях фазы () волновой функции возникает дополнительная свободная энергия , где - удельная плотность сверхтекучей компоненты - играет роль коэффициента жёсткости. Бсли переход в упорядоченное состояние является переходом второго рода, то в точке перехода .

Примером, когда при упорядочении не возникает дополнительной жесткости, является упорядочивание сплава. В этом случае в результате упорядочения нарушается не непрерывная, а дискретная симметрия относительно трансляций на периоды исходной решетки.

Упорядочение в одномерных и двумерных системах

Упорядочение в одномерных (цепочки) и двумерных (плёнки) системах имеет ряд особенностей: как правило, дальний порядок при любой конечной температуре в них отсутствует, но при низких температурах есть ближний порядок с большим радиусом корреляции R_c. Если при упорядочении нарушается дискретная симметрия, то в двумерном случае возможен дальний порядок. В одномерном же случае дальнего порядка нет, но , где J - "выигрыш" в энергии при упорядочении. Если при упорядочении нарушается непрерывная симметрия, то дальнего порядка нет и в двумерных и в одномерных системах; в двумерном или в одномерном случае.

Если между цепочками или пленками есть слабое взаимодействие (не путать с фундаментальным слабым взаимодействием), то при высокой температуре отсутствуют и дальний и ближний порядок, при понижении температуры возникает область ближнего порядка с большим R_c и при самых низких температурах возникает дальний порядок (см. Квазиодномерные соединения, Квазидвумерные соединения).

Многократное упорядочение

Вещество, в котором уже произошло кристаллическое упорядочение, может при понижении T испытать вторичное упорядочение, приводящее к дальнейшему понижению симметрии как в координационном расположении атомов (сегнетоэлектрики, сплавы), так и в ориентации магнитных моментов (магнетики). Если отношение периодов новой структуры и кристаллической решетки является рациональным числом, то возникшую дополнительную структуру называют соизмеримой и говорят, например, о магнитной элементарной ячейке. Примером несоизмеримой структуры является решетка вихрей Абрикосова в сверхпроводниках, периоды которой определяются напряженностью внешнего магнитного поля.

С дополнительными жесткостями часто оказываются связанными дополнительные ветви коллективных воз6уждений. Так, в кристаллах наблюдаются поперечные звуковые волны, физически невозможные в жидкостях, в ферромагнетиках - спиновые волны, в сверхтекучем He^II - второй звук.

Экспериментальные методы

В некоторых случаях удается непосредственно измерить параметр порядка, например намагниченность или спонтанную поляризацию. Другой способ дают дифракционные методы - нейтронографические или рентгенографические исследования корреляционных функций удельной плотности или магнитного момента (см. Нейтронография, Рентгеновский структурный анализ). В случае дальнего порядка нейтроно- или рентгенограммы обнаруживают узкие брэгговские пики, интенсивность которых пропорциональна квадрату объёма V образца. В случае же ближнего порядка эти пики "размываются" на ширину, обратно пропорциональную корреляционному радиусу R_c, а их интенсивность пропорциональна R_cV. В тех же случаях, когда R_c велико, различить ближний и дальний порядок становится трудно (см. Нейтронография структурная, Магнитная нейтронография).

Ряд методов, например, рассеяние света на звуковых и других длинноволновых колебаниях, позволяет обнаружить коллективные колебания и, следовательно, дополнительные жесткости (см. Комбинационное рассеяние света). С помощью этих методов можно различить дальний и ближний порядок, если есть возможность исследовать коллективные колебания достаточно низких частот, т. к. высокочастотные колебания существуют и в случае ближнего порядка (например, сдвиговые волны в жидкости).