<< Интерференция в оптике. Опыт | Оглавление | Калибровка интерферометра >>
Радиоинтерферометр
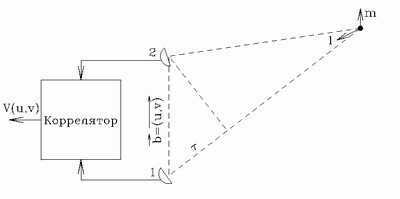
Рассмотрим систему из двух радиотелескопов (рис. 3). В
отличие от оптики в радиодиапазоне возможна реализация
амплитудного детектора излучения, то есть мы можем регистрировать
непосредственно 
, а не
. Поэтому можно
свести сигнал с обeих антенн на специализированный компьютер,
называемый коррелятором, где будет вычисляться корреляция,
присутствующая в выражении для интенсивности. Таким образом, в
радиоинтерферометре непосредственно измеряется функция видности
без анализа интерференционной картины. Функцию видности удобно
определить следующим образом:
.Это определение отличается от введенного ранее постоянным множителем (
), функция видности является функцией вектора
базы (
на рис. 3), то есть вектора
расстояния между радиотелескопами 1 и 2. Как и в случае с опытом
Юнга для протяженного источника, распределение яркости по
источнику связано с функцией видности преобразованием Фурье
(формулы могут быть получены аналогично), однако теперь
преобразование Фурье двумерно, так как мы в данном случае не
ограничиваемся случаем линейного источника.
.Вместо одной пространственной частоты
, равной
расстоянию между щелями в опыте Юнга, функция видности зависит
теперь от двух пространственных частот 
и 
, которые являются
проекциями вектора базы
на координатные оси в
картинной плоскости. В этой же системе координат с центром в
источнике исследуется и распределение яркости 
, 
и
- направляющие косинусы. Удобно выбрать для оси (и
соответственно ) направление на восток, а для оси (и
соответственно ) - на север. Таким образом, смещение по
будет отвечать смещению по прямому восхождению, а смещение по
- смещению по склонению. Обычно также координаты и
базы интерферометра измеряют в единицах длин волн, тогда уравнение
(7) принимает классическую форму преобразования Фурье.
Чтобы получить распределение яркости по источнику, необходимо
измерить функцию видности для всех значений и . Реально это
осуществить нельзя, поэтому измеряемое изображение будет искажено.
Если ввести функцию 
, которая равна 1 в тех точках
-плоскости, для которых была измерена функция видности, а
иначе - равна 0, тогда измеряемую функцию видности
можно представить в виде
.Функция
называется заполнением -плоскости.
По известной теореме
о свертке преобразования Фурье (см., например, [1]), полученное
обращением (7)
изображение будет сверткой истинного изображения и
Фурье-образа , который называется "грязной диаграммой направленности".
Существуют различные методы восстановления изображения, однако в любом
случае желательно получить как можно лучшее заполнение -плоскости в
процессе эксперимента, чтобы облегчить работу этим методам.
|
 |
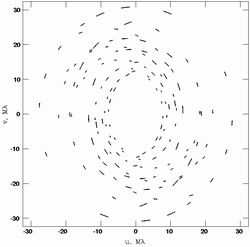Рис. 4.
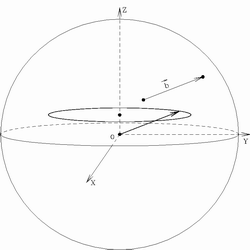
Заполнение -плоскости. На рисунке слева показано
формирование трека концом вектора базы за счет вращения Земли.
Справа - пример реального заполнения -плоскости в
эксперименте с пятью антеннами. Поскольку источник наблюдался в
серии коротких экспозиций, дуги эллипсов не сплошные
Заполнение -плоскости и соответственно измерение функции
видности для различных и осуществляется обычно за счет
вращения Земли. В координатах, связанных с источником, вектор базы
вращается, так что его конец описывает в
пространстве дугу окружности (рис. 4). В проекции на
картинную плоскость это дает дугу эллипса. Увеличение количества
антенн в интерферометре приводит, как правило, к увеличению числа
баз, что также улучшает заполнение -плоскости. На рис.4 справа приведено реальное заполнение -плоскости в
эксперименте с пятью антеннами. Координаты базы и связаны
следующим образом с ее геоцентрическими координатами
, где ось 
направлена в плоскости экватора в направлении
меридиана (
), ось 
- на восток (
), а ось 
- в направлении северного полюса мира
(
):
,где
и 
- часовой угол и склонение источника соответственно.
Из формулы (9) следует важное следствие: для околоэкваториальных
источников базы Запад-Восток (
) не чувствительны к склонению
источника. Иными словами, на -плоскости эллипс вырождается в прямую
линию 
. Если все базы интерферометра расположены в направлении
Запад-Восток, то синтезированная диаграмма направленности
(обратное Фурье-преобразование от заполнения -плоскости) имеет
бесконечную ширину по оси склонений для экваториальных источников.
<< Интерференция в оптике. Опыт | Оглавление | Калибровка интерферометра >>
|
Публикации с ключевыми словами:
Радиоинтерферометр
Публикации со словами: Радиоинтерферометр | |
См. также:
Все публикации на ту же тему >> | |
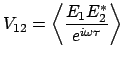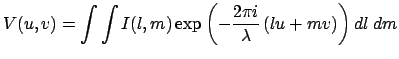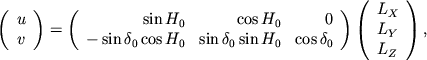