Астронет > Я.Б.Зельдович, "Возможно ли образование Вселенной "из ничего"?

по текстам по ключевым словам в глоссарии по сайтам перевод по каталогу

Возможно ли образование Вселенной "из ничего"?

<< Астрофизические выводы ... | Оглавление | Послесловие >>

О СПОНТАННОМ РОЖДЕНИИ

Знаменитый до революции юморист А. Аверченко начинал свою "Всемирную историю" словами: "История мидян темна и непонятна. Ученые делят ее, тем не менее, на три периода: первый, о котором ровно ничего не известно. Второй, который последовал за первым. И, наконец, третий период, о котором известно столько же, сколько и о первых двух".

Боюсь, что последняя часть моей статьи о ранней истории Вселенной будет похожа на древнюю историю человечества в изложении А. Аверченко. До сих пор мы выясняли только принципиальную возможность рождения Вселенной. Что можно сказать о конкретном механизме этого явления? Придется ограничиться постановкой вопросов.

Прежде всего, словом "ничего", "из ничего" можно придавать разные трактовки. Можно представить себе пустое плоское пространство Минковского - само по себе такое решение уравнений ОТО существует и оно вечное. Рождение можно было бы представить себе наподобие серии картинок (см. рис).

Рождение замкнутой Вселенной (шарик на последней части IV рис.) из плоского мира Минковского (М на стадии I). На промежуточных стадиях, вдали от флуктуации, приводящей к рождению (отщеплению) шарика, метрика остается плоской ("минковской").

Надо только помнить, что в них речь идет об одномерной аналогии. Изображать рождение трехмерного замкнутого пространства (из трехмерного сечения) пространства Минковского я не умею. Время t&nbap; есть параметр, отличающий одну часть картинки (I-IV) от другой. После отделения замкнутой области остающееся пространство снова плоское. Но ведь оно плоское только в классическом пределе. В действительности в квантовой теории метрика пространства тоже флуктуирует подобно тому, как осциллятор имеет определенную среднюю кинетическую и такую же потенциальную энергию, не равную нулю в нижнем энергетическом состоянии.

Таким образом, на приведенном рисунке речь идет о флуктуации - но о флуктуации настолько большой, что меняется сама топология, пространство раздваивается. Рассчитывать такие флуктуации сегодня мы не умеем. Напомню, что сами свойства вакуума (его среднюю энергию, т. е. космологическую постоянную) мы находим только из опыта.

Второй популярный вариант состоит в рассмотрении только одного замкнутого мира (без подстилающего или рождающего его пространства Минковского). Тогда до "начала" не было буквально ничего, никакой метрики, в частности не было и времени.

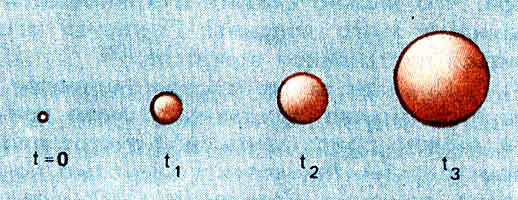Спонтанное рождение мира "из ничего". До момента t = 0 метрика (и, в частности, время) не существовала.

Классические уравнения движения не имеют решения нужного типа. Значит, следует искать квантовомеханические решения. Задача подобна задаче об $\alpha$ -распаде ядра урана или радия. По классической ньютоновской механике $\alpha$ -частица не может пройти весь путь от ядра до бесконечности. Квантовомеханическое решение для $\alpha$ -частицы описывает обе области: "подбарьерную", в которой кинетическая энергия отрицательна (т. е. классическое движение невозможно), и далекую область, в которой существуют оба решения - и классическое, и квантовомеханическое, и они мало отличаются друг от друга.

Подобно теории $\alpha$ -распада строится и квантовомеханическая теория рождения Вселенной. Естественно, задачу сейчас решают лишь в самом грубом приближении, рассматривая всего две величины - радиус замкнутой Вселенной а(t) и скалярное поле $\varphi$ . В квантовой теории вводятся соответствующие импульсы Р_a и Р, строится волновая функция $\Psi(a,\varphi).$ Импульс Р_a = М_eff = f(a)a' - пропорционален скорости расширения, и в классическом пределе можно найти a' = da/dt, а значит, и время

$t = \int \left(\frac{da}{dt}\right)^{-1} da\,.$

Заметим также, что квантовая теория даже в сегодняшнем неразвитом ее состоянии дает аргумент в пользу замкнутой Вселенной (в отличие от бесконечной плоской или открытой Вселенной). Только для замкнутой Вселенной можно определить некое небесконечное значение эффективной массы М_eff. Какой бы формулировкой квантовой механики мы ни пользовались (волновая функция, или "интегрирование по путям", или любой иной), вероятность спонтанного рождения бесконечной Вселенной тождественно равна нулю ^*).

В целом, однако, интерпретация полученных результатов остается не вполне ясной. Квантовомеханические формулы указывают на возможность рождения Вселенной. Представляют интерес результаты в части сравнения вероятности рождения Вселенной с тем или иным начальным значением скалярного поля p. По-видимому, более вероятны большие значения p, обеспечивающие достаточно большую инфляцию на классической фазе. Однако нет интерпретации абсолютного значения волновой функции и вероятности. Есть и более глубокие основания для скепсиса по отношению к конкретным теориям рождения Вселенной "из ничего".

Дело в том, что развитие фундаментальной физики еще явно не закончено! Более того, именно сейчас оживают все более геометризованные теории элементарных частиц. С одной стороны, это. теории, объединяющие бозоны и фермионы, объединяющие внутренние переменные частиц и полей с координатами и преобразованиями Лоренца. В перспективе эти теории должны дать и прямое доказательство существования скалярных полей, а также определить их свойства. Рано или поздно возникнет и теория масс частиц, и физики скажут нам, что такое скрытая масса, которую открыли астрономы. Еще более близкое отношение к вопросу о рождении Вселенной имеют гипотезы о пространстве-времени высокой размерности. Еще в конце 20-х годов была сформулирована идея, согласно которой есть одна "лишняя" координата Х₄, свернутая в кольцо длиной l=2 $\pi$ R, где R - радиус кольца^**). Схематически ситуация изображена на рисунке. Три пространственных координаты X₁, Х₂, Х₃ - заменены одной Х вдоль трубки.

В квантовой теории движение вдоль Х₄ или локализация частицы пр координате Х₄ требуют гигантских энергии. Поэтому во всех опытах вплоть до самых больших энергий, 10¹⁷ или даже 10¹⁹ ГэВ (сравните с 10³ ГэВ на ускорителях 80-х годов), нет движения по особой координате Х₄ (или от Х₄ до Х₉). Теоретики говорят, что в низкоэнергетическом пределе пространство-время остается эффективно четырехмерным. Если к тому же ограничиваться размерами, малыми по сравнению с астрономическими, то пространство и время описываются старой доброй метрикой Минковского.

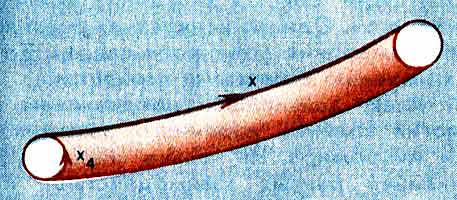Схематичное изображение пространства Капуцы-Клейна. Показано сечение одного заданного значения времени X₀= const, три пространственные координаты X₁, Х₂, Х₃ заменены одной - X. В итоге получилась двумерная поверхность трубки с координатами X, X₄ на поверхности.

И тем не менее, введение в рассмотрение дополнительных измерений - Х₄ в простейшем примере - не проходит бесследно. Можно рассмотреть малые изменения метрики, при которых координатная ось дополнительного измерения Х₄ предполагается не перпендикулярной координатной сетке основных (макроскопических) измерений. Оказывается, что эффективно такое предположение эквивалентно появлению электромагнитного поля в обычном пространстве.

Увеличение числа компактифицированных ("свернутых") переменных с 1 до 6 или 7 (переход к 10-мерному исходному пространству-времени) дает возможность ввести не только электромагнитное поле, но и те поля (W^±, Z°), которые описывают слабое взаимодействие, и поля (глюонные), которые описывают сильное взаимодействие. К тому же, теория суперсимметрии, объединяющая бозонные поля (такие, в частности, как электромагнитное) и фермионные поля (такие, как электрон-позитронное), тоже "геометрична", она вводит новые - удивительные, но геометрические переменные. Мечта А. Эйнштейна о геометризации всей физики сегодня представляется гораздо более реальной, чем это казалось всего 5 или 10 лет назад.

Но почему я пишу обо всем этом в космологической статье?

Первая (не самая главная) причина состоит в том, что мы, наконец, присутствуем при рождении теорий, для которых скалярные поля являются необходимым следствием. О значении скалярных полей уже говорилось - без них не было бы инфляционной Вселенной. Поляризация вакуума как источник энергии и отрицательного давления для инфляции (раздувания) Вселенной, есть тоже разновидность скалярного поля.

Однако более существен и более специфичен второй аспект влияния теорий с "лишними" измерениями на космологию. В момент рождения в замкнутом мире пространственные переменные X₁, Х₂, Х₃ меняются в очень узких пределах порядка 0 < 2 $\alpha$ a(t), где a(t) стремтся к 0 при t, стремящемся к 0. Естественно предположить в таком случае, что в действительности Вселенная рождается симметричной по всем пространственным переменным (размерность Д = 5 или выше). Разделение геометрических переменных на "внутренние", т. е. компактифицированные, Д = 4 переменные и на обычные геометрические три переменные и время происходит лишь позже. Это разделение представляет собой типичное спонтанное (самопроизвольное) нарушение симметрии! Первоначально мы имеем, например, 9-мерный "шар", все направления в котором эквивалентны, а позже 6 измерений застывают с a₄-a₉ (их характерные размеры порядка 10^-33 см) ^***), а три измерения растут экспоненциально и, в конце концов, становятся больше 5000 Мпк = 10²⁸ см, т. е. больше всей наблюдаемой области Вселенной. Намерения у нас остались те же, что и раньше,- описатьрождение Вселенной "из ничего". Однако конкретная реализация этого намерения становится совсем другой по сравнению с первыми вариантами.

Рождение симметричного мира с координатами X₄ и X₁, Х₂, Х₃ при "замораживании" X₄ (в момент t₂). Этот рисунок создает у читателя неправильное впечатление о неоднородности пространства (большая кривизна на концах эллипса). Однако нужно помнить, что в многомерной геометрии существуют пространства (так называемые решения Бланки), однородные, но с разной кривизной по разным направлениям. К сожалению, я не умею изображать их на плоскости рисунка.

Итак, дальнейшее продвижение космологии требует коренного развития физики микромира. Не только "Великое объединение" разных взаимодействий, но и предстоящее "Самое великое объединение" микромира и космологии - такова наиболее фундаментальная и амбициозная программа конца XX века.

<< Астрофизические выводы ... | Оглавление | Послесловие >>

Публикации с ключевыми словами: Космология - спонтанное рождение Вселенной - законы сохранения - физика элементарных частиц
Публикации со словами: Космология - спонтанное рождение Вселенной - законы сохранения - физика элементарных частиц

См. также:

Подтвержденная прецессия мюонов остается необъяснимой

Разложение далекого света

Формирование галактик в магнитной Вселенной

"Эффекты" Зельдовича, запечатлённые на нашем небе

Сверхновая 1994D и неожиданная Вселенная

Куда смещается красное смещение?

Самая далекая сверхновая типа Ia

Все публикации на ту же тему >>

Мнения читателей [11]

Версия для печати

Астрометрия - Астрономические инструменты - Астрономическое образование - Астрофизика - История астрономии - Космонавтика, исследование космоса - Любительская астрономия - Планеты и Солнечная система - Солнце