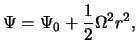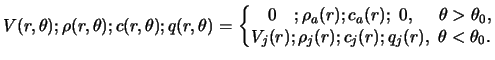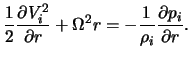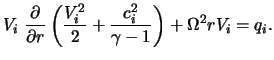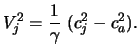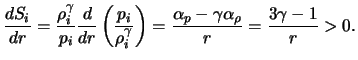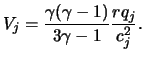Регулярные структуры в конусах ионизации в окрестности активных ядер галактик

---

<< 1. Введение | Оглавление | 3. Методика нелинейного моделирования >>

2. Равновесная модель, основные уравнения
и результаты линейного анализа устойчивости

Обоснование применяемой равновесной модели и ее построение подробно описаны нами в [1], поэтому здесь мы проделаем это конспективно.

Рассмотрение проводим в сферической системе координат , ось которой совпадает с осью симметрии струи, имеющей угол полураствора и скорость течения , где - единичный радиальный базисный вектор. Среду моделируем идеальным газом с уравнением состояния

где и - невозмущенные (равновесные) давление и плотность соответственно; - адиабатическая скорость звука; индекс принимает значение внутри струи и снаружи; показатель адиабаты предполагаем одинаковым для вещества струи и окружающего ее газа.

В околоядерной области струя погружена в распределенную массу звездного балджа, который в первом приближении можно считать сфероидальным; кроме того, для галактик рассматриваемого типа (например, NGC 5252) вообще характерна мощная сфероидальная подсистема. На участке, совпадающем по радиальной координате с участком твердотельного вращения галактического диска, гравитационный потенциал можно с хорошей точностью полагать квадратичным по радиусу: . Считаем гравитационное поле сферически симметричным, с центром, совпадающим с началом координат. Радиальную зависимость гравитационного потенциала представим следующим образом:

где - угловая скорость вращения газа в околоядерной области диска, - нормировочная постоянная.

Газ вне струи считаем неподвижным. Учтем возможность нагрева газа струи излучением ядра: , где - количество энергии, поглощаемое единицей массы вещества в единицу времени; - функция нагрева, - функция охлаждения, зависящие только от температуры . В равновесном состоянии вне струи .

Пространственное распределение характеризующих невозмущенное течение параметров модели имеет вид

Полагаем, что струя удерживается давлением окружающего газа и, следовательно, при выполняется

Последнее соотношение далее практически не используется непосредственно; его выполнение необходимо для реализации течения с .

Радиальные зависимости в (3) определяются невозмущенным балансом сил. Из -компоненты уравнения Эйлера в принятых предположениях следует

Из уравнения неразрывности вытекает

В уравнении (6) - темп потери массы системой в телесный угол раствором в один стерадиан - является свободным параметром.

Уравнение баланса энергии с учетом (1) и уравнения неразрывности для рассматриваемого случая приводится к виду

Система (4)-(7) замыкается уравнением состояния (1).

Решения этой системы ищем в степенном виде: , где  - любой из параметров, характеризующих систему. Из (5) с учетом (1) следует ; соответственно находим

Для сферически симметричного потенциала скорость вещества
в струе и скорости звука в струе и в окружающей ее атмосфере оказываются связаны зависимостью

Таким образом, , где - число Маха струи, т. е. струя дозвуковая. Одновременно с этим может выполняться даже , что делает теоретически возможным существование ударных волн в окружающей струю среде, обусловленных развитием неустойчивости на границе струи, поскольку , т. е. вещество струи всегда более горячее и разреженное, чем окружающая среда, что не противоречит наблюдениям [2]-[5].

С учетом того, что , построенная модель отвечает устойчивому к конвективным движениям распределению энтропии , поскольку

Подстановка степенных радиальных зависимостей в (5) и (7) и сравнение полученных выражений приводит к следующему результату:

Таким образом, скорость вещества в струе однозначно определяется его температурой и нагревом внешним излучением. Для выбросов из активных ядер галактик последний весьма значителен, так как они интенсивно подсвечиваются излучением ядра [2]-[5].

Учитывая (8) определяем, что для реализации построенной модели необходимо

где и - постоянные; - внутренняя энергия газа (для дальнейших выкладок удобнее выразить нагрев и охлаждение не через температуру, а через внутреннюю энергию, используя тот факт, что для идеального газа ). Второе соотношение в (12) в широком диапазоне температур (практически до ) великолепно согласуется с зависимостью , характерной для фотоионизованного газа сейфертовских галактик [9], [15]. Линейная зависимость функции нагрева от температуры также является хорошей аппроксимацией.

Далее рассматривается устойчивость построенной нами модели к малым возмущениям вида

Исходя из необходимости сохранения потока энергии возмущений через сферу произвольного радиуса ( ), определяем, что показатель степени радиальных зависимостей амплитуд возмущений , где - по-прежнему показатель степени для равновесных величин; - показатель степени для гравитационного потенциала. Важно, что решения линеаризованной системы уравнений газовой динамики вида (13) являются точными.

Проведенный линейный анализ устойчивости позволил нам сделать следующие выводы:

1. Конические выбросы вещества, находящиеся в поле квадратичного гравитационного потенциала и подобные наблюдаемым в ряде сейфертовских галактик, неустойчивы относительно резонансно-волноводного развития широкого спектра пинчевых и винтовых внутренних гравитационных мод.

2. Характерное время роста амплитуды этих мод крайне слабо зависит от угла раствора струи в широком диапазоне углов.

3. Динамическое охлаждение высвечиванием полностью подавляет все гравитационно-акустические моды, слабо влияет на неустойчивые поверхностные моды Кельвина-Гельмгольца, приводит к затуханию волноводно-резонансных внутренних гравитационных мод, распространяющихся относительно вещества струи от источника выброса, и, наоборот, значительно усиливает неустойчивость таких мод, распространяющихся к источнику.

4. Указанное усиление имеет характер радиативно-диссипативной неустойчивости мод отрицательной плотности энергии.

5. За формирование наблюдаемых регулярных структур в конусах излучения в окрестности ядер сейфертовских галактик могут быть ответственны только поверхностные неустойчивые моды и медленные (распространяющиеся по струе к источнику) волноводно-резонансные внутренние гравитационные моды. Скорости этих мод вдоль границ струи превышают характерную скорость звука в окружающей атмосфере, что позволяет предполагать возможность их эволюции в ударные волны.

6. При малых углах раствора струи наиболее вероятно развитие основной гармоники пинчевой моды внутренних гравитационных волн в коротковолновой области (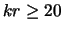), а в более длинноволновом диапазоне ( 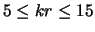) - основной гармоники первой винтовой моды.

   Из-за различной пространственной локализации первой винтовой и пинчевой мод развитие одной из них не должно фатально сказываться на другой.

---

<< 1. Введение | Оглавление | 3. Методика нелинейного моделирования >>

Публикации с ключевыми словами: Ядра галактик - джет - Сейфертовская галактика Публикации со словами: Ядра галактик - джет - Сейфертовская галактика
См. также: M106: спиральная галактика со странным ядром Порфирион: самый длинный джет от черной дыры Галактика, джет и знаменитая черная дыра Аккрецирующая черная дыра с джетом HH 211: джеты от формирующейся звезды Три галактики в Драконе В рукавах NGC 1097 Все публикации на ту же тему >>