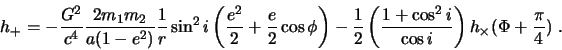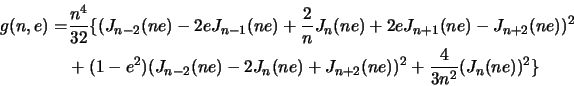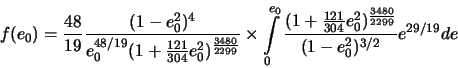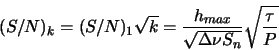Конкурс "Астронет-2001"
<< 2. Стационарная функция распределения | Оглавление | 4. Обсуждение >>
- 3.1 ГВ-излучение от одной системы
- 3.2 Стохастический ГВ-сигнал от стационарного ансамбля двойных звезд
- 3.3 Широкополосный ГВ-сигнал
3. ГВ от компактных двойных нейтронных звезд на эллиптических орбитах
3.1 ГВ-излучение от одной системы
3.1.1 Случай некруговой орбиты
Рассмотрим ГВ-излучение от двойной системы, состоящей из двух компактных звезд с массами
Усредняя по ориентации орбиты
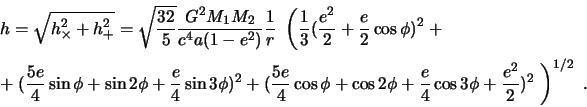 |
(3.3) |
В более простом случае ![]() , амплитуда ГВ от источника, находящегося на расстоянии
, амплитуда ГВ от источника, находящегося на расстоянии ![]() ,
усредненная по ориентации орбиты и периоду записывается в виде
,
усредненная по ориентации орбиты и периоду записывается в виде
При излучении ГВ будут уносить из системы энергию и импульс.
Энергия ![]() , переносимая ГВ в направлении ее распространения
через площадку
, переносимая ГВ в направлении ее распространения
через площадку ![]() за время
за время ![]()
Полная энергия, излучаемая отдельным источником в единицу времени находится интегрированием потока (3.5) по всем направлениям.
| (3.6) |
В спектральном представлении, количество энергии излучаемой в единицу
времени на ![]() -гармонике (см. Зельдович и Новиков 1967) можно записать
-гармонике (см. Зельдович и Новиков 1967) можно записать
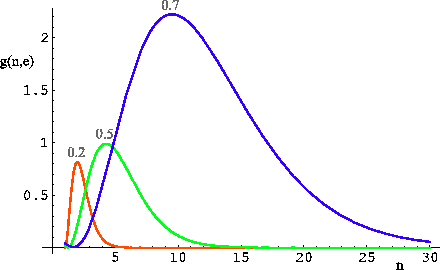 |
| Рис. 3.1
Функция |
3.1.2 Длительность слияния двойной системы
Рассмотрим двойную систему на круговой орбите.
Такая система теряет гравитационную энергию связи
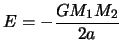 в виде
излучения гравитационных волн (3.7).
При этом полуось орбиты уменьшается (в квадрупольном приближении) в соответствии
с уравнением.
в виде
излучения гравитационных волн (3.7).
При этом полуось орбиты уменьшается (в квадрупольном приближении) в соответствии
с уравнением.
Это время и есть длительность слияния двойной системы.
В случае некруговой орбиты необходимо рассматривать систему уравнений (2.2)-(2.3). В результате получим
Время слияния двойной системы с начальным эксцентриситетом отличным от нуля меньше,
чем для системы на круговой орбите с той же начальной полуосью ![]() .
.
Это может быть понятно из следующих соображений.
В случае эллиптичной орбиты потери энергии из-за излучения ГВ больше, чем в случае
круговой орбиты на фактор
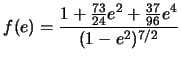 ,
который очень быстро растет при
,
который очень быстро растет при ![]() .
А гравитационная энергия связи двойной системы
зависит только от большой полуоси системы и не зависит от эксцентриситета.
Излучая гравитационные волны, система становится более тесной и круговой
(
.
А гравитационная энергия связи двойной системы
зависит только от большой полуоси системы и не зависит от эксцентриситета.
Излучая гравитационные волны, система становится более тесной и круговой
(
![]() и
и
![]() - имеют отрицательный знак).
При уменьшение эксцентриситета уменьшается и фактор
- имеют отрицательный знак).
При уменьшение эксцентриситета уменьшается и фактор ![]() , и к моменту
слияния орбита становится почти круговой. Уменьшение фактора
, и к моменту
слияния орбита становится почти круговой. Уменьшение фактора ![]() и
зависимость
и
зависимость ![]() определяет интеграл (3.13).
определяет интеграл (3.13).
3.2 Стохастический ГВ-сигнал от стационарного ансамбля двойных звезд
Как уже говорилось выше, в Галактике значительная часть звезд
входит в состав двойных систем.
В случае большого числа ![]() независимых одинаковых источников
на одном и том же расстоянии
независимых одинаковых источников
на одном и том же расстоянии ![]() , которые излучают
ГВ со случайными фазами, детектор будет регистрировать гравитационно-волновой шум,
уровень которого
, которые излучают
ГВ со случайными фазами, детектор будет регистрировать гравитационно-волновой шум,
уровень которого
![]() . В случае двойных систем
уровень фона ГВ
. В случае двойных систем
уровень фона ГВ
![]() , где
, где ![]() - темп слияния
этих систем.
- темп слияния
этих систем.
Наиболее многочисленна популяция галактических двойных белых карликов (Бендер 1990, Бендер 1997, Постнов и Прохоров 1998), двигающихся по круговым орбитам. Уровень стохастического фона ГВ от этих систем достаточен, для того, чтобы его можно было зарегистрировать космическим интерферометром LISA. Образование и методы вычисления уровня фона рассмотрены в работах Постнов и Прохоров 1998, Грищук и др. 2001.
В случае некруговых орбит ГВ-светимость выше, нежели в круговом случае.
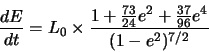
Кроме того, такие системы излучают не на одной частоте (удвоенной орбитальной),
а в широком диапазоне частот.
где
3.2.1 Образование стохастического фона от двойных систем на эллиптических орбитах.
Рассмотрим некоторый интервал частот (в дальнейшем - бин)
![]() ,
такой, что
,
такой, что
![]() .
В этот бин попадает излучение от двойных систем, которые имеют орбитальную
частоту
.
В этот бин попадает излучение от двойных систем, которые имеют орбитальную
частоту
![]() и излучают на первой гармонике.
и излучают на первой гармонике.
Число таких систем можно найти из стационарной функции распределения
![]() . Также в этот частотный интервал попадает излучение
от систем с орбитальной частотой
. Также в этот частотный интервал попадает излучение
от систем с орбитальной частотой
![]() ,
которые излучают на второй гармонике. И так далее.
Суммарная энергия, излучаемая в единицу времени на частоте
,
которые излучают на второй гармонике. И так далее.
Суммарная энергия, излучаемая в единицу времени на частоте ![]() в
частотный интервал
в
частотный интервал ![]()
Стоит заметить, что при увеличении номера гармоники уменьшается интервал орбитальной
частоты системы
 , излучение от которой может попасть
в наблюдаемый частотный бин.
, излучение от которой может попасть
в наблюдаемый частотный бин.
Осталось только пояснить, что такое ![]() . Амплитуда высоких гармоник
. Амплитуда высоких гармоник ![]() быстро уменьшается (см. рисунок 3.1), и мы останавливаем
суммирование по гармоникам при
быстро уменьшается (см. рисунок 3.1), и мы останавливаем
суммирование по гармоникам при ![]() , которое определим следующим образом.
, которое определим следующим образом.
![]() , таким образом вклад от гармоники
, таким образом вклад от гармоники ![]() будет
в
будет
в ![]() раз меньше вклада от гармоники
раз меньше вклада от гармоники ![]() . При расчетах использовались значения
. При расчетах использовались значения
![]() . При уменьшении
. При уменьшении ![]() увеличивается число гармоник,
попадающих в частотный бин, но практически не меняется число наиболее мощных гармоник в бине.
увеличивается число гармоник,
попадающих в частотный бин, но практически не меняется число наиболее мощных гармоник в бине.
3.2.2 Стационарный стохастический фон от сливающихся НЗ.
Рассчитаем ГВ-фон для простой модели, в которой все двойные системы
образуются в одной точке фазового пространства ![]() с темпом рождения (и слияния)
с темпом рождения (и слияния)
![]() год
год![]() . Следовательно, начальная функция распределения имеет вид
дельта-функции. Рассчитав стационарную функцию распределения можно построить спектр ГВ-фона,
изображенного на рисунках
3.3-3.4 для
. Следовательно, начальная функция распределения имеет вид
дельта-функции. Рассчитав стационарную функцию распределения можно построить спектр ГВ-фона,
изображенного на рисунках
3.3-3.4 для
![]() и
и ![]() и
и ![]() соответственно.
соответственно.
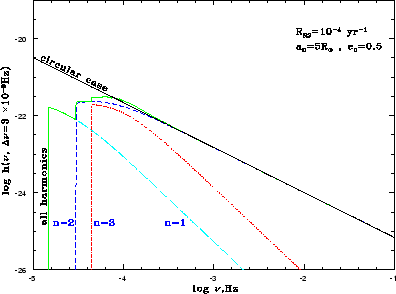 |
| Рис. 3.3
ГВ-фон и вклады в него первой, второй и третьей гармоники. Все системы
формируются с
|
Кроме того, на рисунках 3.3-3.4 изображены вклады первых трех гармоник в общий ГВ-фон. Видно, что увеличение начального эксцентриситета сильно влияет на вид спектра до некоторой частоты, при которой эксцентриситеты двойных, формирующих ГВ-фон, становятся незначительными. На частотах выше этой частоты только излучение на второй гармонике от почти круговых орбит определяет общий спектр. Немонотонная зависимость общего спектра и вкладов отдельных гармоник от частоты является следствием немонотонной зависимости энергии излучаемой на каждой гармонике от эксцентриситета.
Теперь рассмотрим стохастический фон ГВ от галактических двойных НЗ на эллиптических
орбитах. Предполагаем, что все источники находятся на одном расстоянии,
а именно ![]() кпк (см. часть 2.1).
кпк (см. часть 2.1).
На каждой частоте мы суммируем ГВ-поток от всех гармоник попадающих в частотный
бин
![]() Гц от двойных систем с посчитанной стационарной
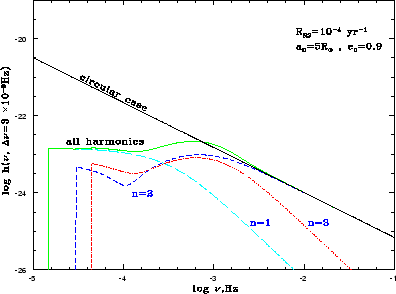
функцией распределения (см. (2.5)). Результирующий фон изображен на рисунке 3.5
в терминах безразмерной амплитуды вариации метрики
Гц от двойных систем с посчитанной стационарной
функцией распределения (см. (2.5)). Результирующий фон изображен на рисунке 3.5
в терминах безразмерной амплитуды вариации метрики ![]() , которую мы определяем
соотношением.
, которую мы определяем
соотношением.
 |
| Рис. 3.5
ГВ-фон от сливающихся двойных нейтронных звезд в нашей Галактике с темпом слияния
|
Как и ожидалось, уровень стохастического фона, образованный сливающимися двойными
нейтронными звездами, лежит ниже уровня стохастического фона сливающихся белых карликов
главным образом из-за малого темпа слияния ![]() .
Большие гармоники от некруговых систем дают основной вклад в общий фон
на низких частотах, начиная с частоты
.
Большие гармоники от некруговых систем дают основной вклад в общий фон
на низких частотах, начиная с частоты
![]() Гц вычисленный фон практически
не отличается от фона, который бы формировали двойные НЗ на круговых орбитах
с таким же темпом слияния
Гц вычисленный фон практически
не отличается от фона, который бы формировали двойные НЗ на круговых орбитах
с таким же темпом слияния
![]() год
год![]() .
.
Уровень внегалактического фона от двойных нейтронных звезд даже с учетом сильной зависимости темпа звездообразования от красного смещения и космологических эффектов не может составлять более чем 10% от уровня галактического фона (Косенко и Постнов 1998, Шнайдер 2001) и поэтому его рассматривать не будем.
В предположении стационарности уровень фона на частотах выше ![]() также имеет физический смысл.
Действительно, при большом количестве (
также имеет физический смысл.
Действительно, при большом количестве (
![]() ) наблюдений длительностью
один год каждое, усредненный спектр по всем этим наблюдениям
и составит стационарный стохастический фон ГВ.
На рисунке 3.5 изображен длинными штрихами.
) наблюдений длительностью
один год каждое, усредненный спектр по всем этим наблюдениям
и составит стационарный стохастический фон ГВ.
На рисунке 3.5 изображен длинными штрихами.
3.2.3 Предельная частота
Кроме уровня фона есть еще одна важная величина, которая характеризует стохастический фон.
Это предельная частота ![]() , т.е. такая частота, выше которой
индивидуальные источники можно будет разрешить за время наблюдении
, т.е. такая частота, выше которой
индивидуальные источники можно будет разрешить за время наблюдении ![]() год.
Таким образом, предельная частота определяет границу, при наблюдениях на частотах выше
которой принципиально возможно разрешить индивидуальные источники, а также
детектировать более слабые
стохастические фоны (например, реликтовые гравитационные волны, несущие
информацию о ранних стадиях развития Вселенной
год.
Таким образом, предельная частота определяет границу, при наблюдениях на частотах выше
которой принципиально возможно разрешить индивидуальные источники, а также
детектировать более слабые
стохастические фоны (например, реликтовые гравитационные волны, несущие
информацию о ранних стадиях развития Вселенной
![]() сек, см. Грищук и др. 2001).
сек, см. Грищук и др. 2001).
Оценку ![]() можно получить из следующих соображений. Рассмотрим узкий интервал частот
можно получить из следующих соображений. Рассмотрим узкий интервал частот
![]() . Частота излучения от двойных систем, вследствие уноса ГВ энергии
и углового момента, увеличивается, и излучение от определенного источника через
некоторое время перестанет попадать в первоначальный частотный бин.
. Частота излучения от двойных систем, вследствие уноса ГВ энергии
и углового момента, увеличивается, и излучение от определенного источника через
некоторое время перестанет попадать в первоначальный частотный бин.
Пусть с темпом ![]() - источники появляются в частотном окне, и находятся
там время
- источники появляются в частотном окне, и находятся
там время
![]() . Таким образом, число систем в этом интервале частот
. Таким образом, число систем в этом интервале частот
 .
Из условия
.
Из условия
![]() можно определить
можно определить ![]() .
.
Для галактической популяции сливающихся БК, которые находятся на почти круговых орбитах
(см. Грищук и др. 2001)
Мы будем считать число таких гармоник, вклад которых в ГВ - поток на данной частоте
составляет ![]() от общего потока.
Число таких гармоник
от общего потока.
Число таких гармоник
![]() как функция частоты
как функция частоты ![]() изображена на рисунке
3.6 для различных предполагаемых амплитуд скорости «отдачи» во время
вспышки сверхновой. Предельная частота
изображена на рисунке
3.6 для различных предполагаемых амплитуд скорости «отдачи» во время
вспышки сверхновой. Предельная частота ![]() определяемая из уравнения
определяемая из уравнения
![]() при наших неопределенностях
(
при наших неопределенностях
(![]() ,
, ![]() ,
, ![]() и др.) принимает значение
и др.) принимает значение
![]() Гц, что порядка аналогичной величине для сливающихся БК.
Для сравнения на рисунке 3.6 показано
Гц, что порядка аналогичной величине для сливающихся БК.
Для сравнения на рисунке 3.6 показано
![]() для случая круговых
орбит двойных нейтронных звезд.
для случая круговых
орбит двойных нейтронных звезд.
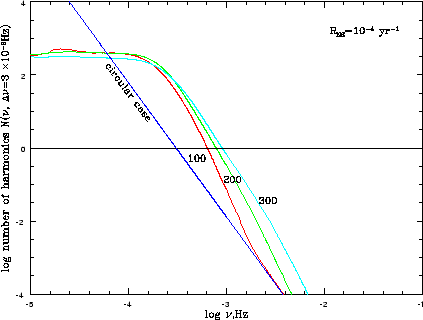 |
| Рис. 3.6
Число гармоник в интервале частот |
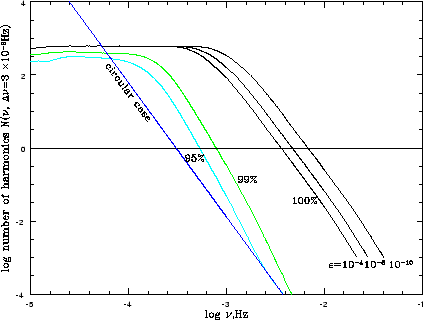 |
| Рис. 3.7
Число наиболее мощных гармоник в бине |
Эффект зависимости от выбранного уровня ГВ-потока от наиболее мощных гармоник
изображен на рисунке 3.7. Увеличение уровня с ![]() до
до ![]() увеличивает
значение
увеличивает
значение ![]() почти на порядок.
почти на порядок.
Теперь рассмотрим частотные бины на частоте ![]() больше предельной частоты
больше предельной частоты ![]() .
Можно ответить на вопрос, у каких из гармоник попадающих внутрь
бина наибольшая вероятность находиться в бине, и у каких она наименьшая. Эта вероятность
определяется номером гармоники и стационарной функцией распределения
.
Можно ответить на вопрос, у каких из гармоник попадающих внутрь
бина наибольшая вероятность находиться в бине, и у каких она наименьшая. Эта вероятность
определяется номером гармоники и стационарной функцией распределения
![]() . Наименее вероятные, это гармоники от систем
с максимальной орбитальной частотой
. Наименее вероятные, это гармоники от систем
с максимальной орбитальной частотой ![]() , излучение от которых попадает в частотный
бин
, излучение от которых попадает в частотный
бин ![]() на первой гармонике. Проведем такую операцию: отбросим
вклад от систем, излучение от которых на первой гармонике
попадает внутрь частотного интервала
на первой гармонике. Проведем такую операцию: отбросим
вклад от систем, излучение от которых на первой гармонике
попадает внутрь частотного интервала
![]() при
при ![]() .
При этом теряется некоторая часть общего ГВ-потока и можно найти новую оценку
предельной частоты
.
При этом теряется некоторая часть общего ГВ-потока и можно найти новую оценку
предельной частоты ![]() . Для частот
. Для частот
![]() проведем
подобную операцию. Здесь наименее вероятной гармоникой будет вторая. Находим соответствующую
этому случаю предельную частоту
проведем
подобную операцию. Здесь наименее вероятной гармоникой будет вторая. Находим соответствующую
этому случаю предельную частоту ![]() . И так далее, отбрасываем вклады от 3-ей,
4-ой,...,
. И так далее, отбрасываем вклады от 3-ей,
4-ой,...,![]() -ой гармоник, пока уровень оставшегося фона не станет меньше уровня чувствительности
детектора.
-ой гармоник, пока уровень оставшегося фона не станет меньше уровня чувствительности
детектора.
Как уже говорилось выше, наименьшая вероятность попадания гармоники в бин у гармоник с малым ![]() ,
но вместе с тем эти гармоники вносят существенный вклад в общий уровень фона. На больших
частотах почти все излучение попадающее в частотный бин определяет вторая гармоника. Соответственно,
уровень фона - именно фона, так как отброшенные гармоники редкие и при этом «мощные» -
для того чтобы их можно было разрешить, будет резко уменьшаться с частотой. Уровень
стохастического фона от двойных нейтронных звезд,
после проведения такой операции изображен на рисунке
3.5 ломаной линией, а предельная частота
,
но вместе с тем эти гармоники вносят существенный вклад в общий уровень фона. На больших
частотах почти все излучение попадающее в частотный бин определяет вторая гармоника. Соответственно,
уровень фона - именно фона, так как отброшенные гармоники редкие и при этом «мощные» -
для того чтобы их можно было разрешить, будет резко уменьшаться с частотой. Уровень
стохастического фона от двойных нейтронных звезд,
после проведения такой операции изображен на рисунке
3.5 ломаной линией, а предельная частота ![]() оказывается порядка
оказывается порядка ![]() мГц.
Конечно, эта кривая не представляет собой реального
стохастического фона ГВ от сливающихся галактических двойных НЗ и дает представление только
о его поведении на частотах больше предельной частоты
мГц.
Конечно, эта кривая не представляет собой реального
стохастического фона ГВ от сливающихся галактических двойных НЗ и дает представление только
о его поведении на частотах больше предельной частоты
![]() мГц.
На частотах ниже предельной уровень стохастического фона определяется
стационарным стохастическим фоном рассчитанным выше.
мГц.
На частотах ниже предельной уровень стохастического фона определяется
стационарным стохастическим фоном рассчитанным выше.
3.3 Широкополосный ГВ-сигнал
ГВ-излучение от двойных звезд нашей Галактики образует стохастический фон
на частотах
![]() Гц и может быть обнаружено космическим интерферометром
LISA. На частотах выше предельной частоты (см. часть 3.2.3)
Гц и может быть обнаружено космическим интерферометром
LISA. На частотах выше предельной частоты (см. часть 3.2.3)
![]() Гц
можно будет регистрировать гравитационные волны от отдельных систем за время наблюдения один год.
Обнаружить ГВ от двойной системы на круговой орбите за год наблюдений, скорее всего не удастся,
так как слишком мала вероятность такого события. Напомним, что темп слияния двойных нейтронных
звезд
Гц
можно будет регистрировать гравитационные волны от отдельных систем за время наблюдения один год.
Обнаружить ГВ от двойной системы на круговой орбите за год наблюдений, скорее всего не удастся,
так как слишком мала вероятность такого события. Напомним, что темп слияния двойных нейтронных
звезд
![]() в год, а белых карликов
в год, а белых карликов
![]() лет
лет![]() .
В тоже время вероятность обнаружить излучение от двойных систем нашей Галактики
в частотном диапазоне
.
В тоже время вероятность обнаружить излучение от двойных систем нашей Галактики
в частотном диапазоне
![]() Гц весьма велика. Это связано с двойными системами
на сильно вытянутых орбитах, излучение от которых происходит на больших гармониках.
Что же представляет из себя это излучение? Максимум излучения ГВ от двойных звезд
на эллиптических орбитах приходится на моменты вблизи прохождения периастра
Гц весьма велика. Это связано с двойными системами
на сильно вытянутых орбитах, излучение от которых происходит на больших гармониках.
Что же представляет из себя это излучение? Максимум излучения ГВ от двойных звезд
на эллиптических орбитах приходится на моменты вблизи прохождения периастра ![]() .
ГВ-излучение от такой систем будет носить характер широкополосных импульсов с периодом повторения
(орбитальным периодом) от десятков минут до нескольких часов в диапазоне частот
.
ГВ-излучение от такой систем будет носить характер широкополосных импульсов с периодом повторения
(орбитальным периодом) от десятков минут до нескольких часов в диапазоне частот
![]() Гц.
Длительность такого импульса определяется временем пролета вблизи периастра, где происходит
интенсивная генерация ГВ. Для больших эксцентриситетов длительность импульса приближенно
равна
Гц.
Длительность такого импульса определяется временем пролета вблизи периастра, где происходит
интенсивная генерация ГВ. Для больших эксцентриситетов длительность импульса приближенно
равна ![]() (
(![]() - скорость движения в периастре), и максимум излучения приходится
на гармонику
- скорость движения в периастре), и максимум излучения приходится
на гармонику
![]() в соответствии с третьим законом Кеплера.
в соответствии с третьим законом Кеплера.
3.3.1 ГВ-сигнал от двойных систем при прохождении периастра
Определим время излучения основной части энергии при движении НЗ вблизи периастра.
Для этого воспользуемся выражением для излучения ГВ от двух точечных масс
на эллиптических орбитах, усредненным по пространственной ориентации орбиты
(Ландау и Лифшиц 1973)
Перейдем от интегрирования по времени ![]() к интегрированию по полярному углу
к интегрированию по полярному углу
Зависимость ![]() и
и ![]() от эксцентриситета изображена на рисунке 3.8.
Видно, что начиная с эксцентриситета
от эксцентриситета изображена на рисунке 3.8.
Видно, что начиная с эксцентриситета ![]() угол
угол
![]() и слабо
меняется при дальнейшем увеличении эксцентриситета. Это может быть понятно из следующих
соображении: периастральное расстояние
и слабо
меняется при дальнейшем увеличении эксцентриситета. Это может быть понятно из следующих
соображении: периастральное расстояние ![]() и фокальный параметр эллипса орбиты
и фокальный параметр эллипса орбиты
![]() при больших эксцентриситетах меняются одинаково
при больших эксцентриситетах меняются одинаково ![]() и, следовательно периастральные части орбит при различных
и, следовательно периастральные части орбит при различных ![]() подобны друг другу.
подобны друг другу.
Также из рисунка 3.8 следует, что при эксцентриситете около ![]()
![]() энергии
высвечивается за
энергии
высвечивается за ![]() орбитального периода. В дальнейшем мы будем брать значение
орбитального периода. В дальнейшем мы будем брать значение ![]() в качестве нижней границы эксцентриситетов двойных звезд, дающих широкополосные импульсы ГВ.
в качестве нижней границы эксцентриситетов двойных звезд, дающих широкополосные импульсы ГВ.
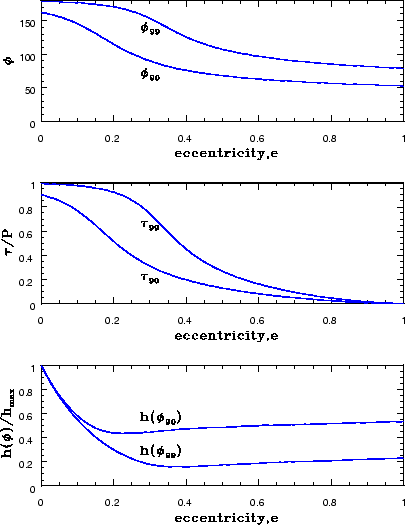 |
| Рис. 3.8
Верхняя панель: полярный угол |
Таким образом, при прохождении периастра двойная НЗ на эллиптической орбите будет излучать
сигнал в широком интервале частот
![]() . Такие импульсы
характеризуются длительностью
. Такие импульсы
характеризуются длительностью ![]() , периодом повторения
, периодом повторения ![]() и амплитудой,
в качестве оценки которой возьмем максимальную безразмерную амплитуду
и амплитудой,
в качестве оценки которой возьмем максимальную безразмерную амплитуду ![]() гравитационной
волны в периастре. Усредняя квадраты амплитуд ГВ-поля различных поляризации по пространственной
ориентации системы, получаем
гравитационной
волны в периастре. Усредняя квадраты амплитуд ГВ-поля различных поляризации по пространственной
ориентации системы, получаем
3.3.2 Особенности детектирования широкополосных ГВ-сигналов
Теперь, если мы хотим расcчитать ожидаемый темп детектирования ГВ-импульсов от двойных систем на эллиптических орбитах, следует точнее определить, что мы будем называть импульсом и записать для такого сигнала отношение сигнал к шуму.
Двойные НЗ на вытянутой орбите, излучение от которых в периастре попадает
в частотный диапазон
![]() Гц, могут иметь орбитальные периоды
от десятков минут до нескольких часов (см. рисунок 3.9).
Гц, могут иметь орбитальные периоды
от десятков минут до нескольких часов (см. рисунок 3.9).
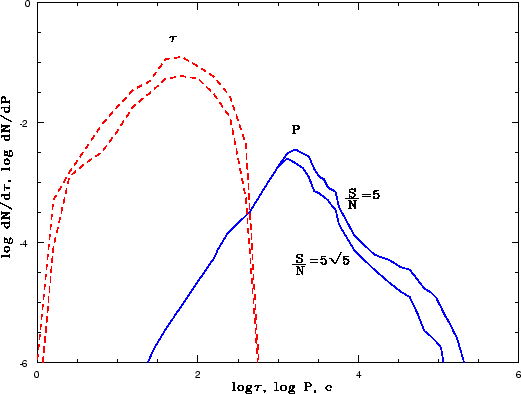 |
| Рис. 3.9
Распределение двойных НЗ, от которых сигнал в периастре превосходит уровень фона
в |
Предполагаем, что изменение энергии и момента импульса системы за один орбитальный
период мало и параметры орбиты не меняются. Это допущение выполняется для рассматриваемых
частот. Тогда за время наблюдения ![]() год сигнал от одной системы будет представлять
периодическую последовательность, состоящую из
год сигнал от одной системы будет представлять
периодическую последовательность, состоящую из ![]() широкополосных импульсов со
случайной фазой относительно начала наблюдении. Также неизвестна пространственная ориентация
системы, направление и расстояние до нее. Следовательно, сигнал на детекторе будет
представлять из себя сумму периодических последовательностей импульсов
широкополосных импульсов со
случайной фазой относительно начала наблюдении. Также неизвестна пространственная ориентация
системы, направление и расстояние до нее. Следовательно, сигнал на детекторе будет
представлять из себя сумму периодических последовательностей импульсов ![]() со случайными
фазами, различными амплитудами и периодами повторений
со случайными
фазами, различными амплитудами и периодами повторений
![]() .
Важно заметить, что в рассматриваемом диапазоне частот такой сигнал не образует стохастического
фона (см. часть 3.2) при частотном разрешении детектора
.
Важно заметить, что в рассматриваемом диапазоне частот такой сигнал не образует стохастического
фона (см. часть 3.2) при частотном разрешении детектора
![]() Гц.
Гц.
Сначала рассмотрим частный случай, когда в рассматриваемом интервале частот имеется только
одна последовательность импульсов. Отношение сигнала к шуму при наблюдении
импульса с длительностью ![]() детектором с чувствительностью
детектором с чувствительностью ![]() (имеет размерность
(имеет размерность
![]() , см. точное определение и обсуждение в обзоре Грищук и др. 2001).
, см. точное определение и обсуждение в обзоре Грищук и др. 2001).
Для периодической последовательности состоящей из ![]() одинаковых импульсов отношение сигнала к
шуму увеличится
одинаковых импульсов отношение сигнала к
шуму увеличится
В качестве реального примера рассмотрим Халс-Тейлоровский пульсар PSR B1913+16 и найдем для него
отношение сигнала к шуму. Орбитальные параметры этой двойной системы состоящей из
двух НЗ (Тейлор, Вайсберг 1989): большая полуось
![]() см, орбитальный период
см, орбитальный период
![]() с, эксцентриситет
с, эксцентриситет ![]() . Массы обеих компонент с большой точностью совпадают
. Массы обеих компонент с большой точностью совпадают
![]() , расстояние до системы
, расстояние до системы ![]() кпк. Усредняя по пространственной
ориентации (будем считать ее неизвестной) находим
кпк. Усредняя по пространственной
ориентации (будем считать ее неизвестной) находим
![]() . Для эксцентриситета
0.617 длительность импульса
. Для эксцентриситета
0.617 длительность импульса
![]() c, ширина импульса в частотном представлении
c, ширина импульса в частотном представлении
![]() мГц, частота максимальной (4-ой) гармоники
мГц, частота максимальной (4-ой) гармоники ![]() мГц.
Отношение сигнала к шуму за год непрерывных наблюдений, оцененное по формуле (3.20)
равно 0.5 (без учета шума от галактических белых карликов, ГВ-фон которых определяет
астрофизический шум на детекторе в данном интервале частот). Видно, что PSR B1913+16
невозможно будет зарегистрировать, и такие источники нам не интересны.
мГц.
Отношение сигнала к шуму за год непрерывных наблюдений, оцененное по формуле (3.20)
равно 0.5 (без учета шума от галактических белых карликов, ГВ-фон которых определяет
астрофизический шум на детекторе в данном интервале частот). Видно, что PSR B1913+16
невозможно будет зарегистрировать, и такие источники нам не интересны.
Теперь рассмотрим галактическую популяцию двойных нейтронных звезд. Воспользовавшись результатами Главы 2, построим начальную и стационарную функции распределения по орбитальными параметрам. Кроме того, на стационарную функцию распределения наложим дополнительные условия, определяющие ее границы на фазовой плоскости.
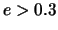 нижняя граница эксцентриситетов двойных звезд, ГВ-излучение от которых
представляется в виде импульсов.
нижняя граница эксцентриситетов двойных звезд, ГВ-излучение от которых
представляется в виде импульсов.
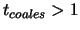 года. Это условие следует из требования постоянства параметров
орбиты.
года. Это условие следует из требования постоянства параметров
орбиты.
-
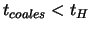 следует из условия стационарности.
следует из условия стационарности.
Выделим на фазовой плоскости ![]() область, в которой находятся системы
излучающие ГВ с амплитудой, дающей отношение сигнал к шуму
область, в которой находятся системы
излучающие ГВ с амплитудой, дающей отношение сигнал к шуму ![]() (по прежнему считаем, что все источники находятся на одинаковом расстоянии
(по прежнему считаем, что все источники находятся на одинаковом расстоянии ![]() кпк).
Интегрируя стационарную функцию распределения по этой области, получаем число таких систем
кпк).
Интегрируя стационарную функцию распределения по этой области, получаем число таких систем
![]() . Понижение порога обнаружения увеличит число таких
систем до 15, в случае
. Понижение порога обнаружения увеличит число таких
систем до 15, в случае ![]() .
.
Поскольку на частотах
![]() Гц именно стохастический фон
от неразрешенных двойных белых карликов определяет уровень шума
на детекторе (уровень фона от других популяции компактных двойных звезд существенно ниже),
мы также учитывали в качестве шума и этот фон.
3.1
Гц именно стохастический фон
от неразрешенных двойных белых карликов определяет уровень шума
на детекторе (уровень фона от других популяции компактных двойных звезд существенно ниже),
мы также учитывали в качестве шума и этот фон.
3.1
Распределение систем по длительности импульсов и
орбитальным периодам приведено на рисунке 3.9. Видно, что наиболее вероятно
обнаружить импульсы с длительностью около 100 секунд от систем с орбитальным периодом
![]() cекунд. Средний эксцентриситет при этом
cекунд. Средний эксцентриситет при этом ![]() .
.
Таким образом, для стационарного распределения двойных НЗ в Галактике, существуют несколько систем с большими эксцентриситетами и орбитальными периодами в диапазоне от нескольких десятков минут до нескольких часов с достаточно высокой амплитудой ГВ в максимуме.
Системы массивный БК+НЗ обладают в среднем значительно меньшим эксцентриситетом
(средний начальный эксцентриситет таких систем
![]() ), поэтому
добавленная нижняя граница по эксцентриситету
), поэтому
добавленная нижняя граница по эксцентриситету ![]() оказывается весьма критичной
для определения числа систем, излучение от которых в периастре в виде широкополосных
импульсов возможно будет регистрировать с большим отношением сигнала к шуму.
В случае стационарного распределения, полного темпа слияния
оказывается весьма критичной
для определения числа систем, излучение от которых в периастре в виде широкополосных
импульсов возможно будет регистрировать с большим отношением сигнала к шуму.
В случае стационарного распределения, полного темпа слияния
![]() год
год![]() и для отношения сигнала к шуму
и для отношения сигнала к шуму ![]() число систем
число систем ![]() , а при
, а при ![]() увеличивается до
увеличивается до ![]() . Видно, что обнаружить такой сигнал за год наблюдении маловероятно.
Наиболее вероятная длительность импульса порядка 300 секунд, а наиболее вероятный
орбитальный период около 1000 секунд, как и для двойных нейтронных звезд.
Стоит заметить, что широкополосные ГВ-импульсы от двойных НЗ и систем БК+НЗ почти
ни чем не отличаются, за исключением их длительности.
. Видно, что обнаружить такой сигнал за год наблюдении маловероятно.
Наиболее вероятная длительность импульса порядка 300 секунд, а наиболее вероятный
орбитальный период около 1000 секунд, как и для двойных нейтронных звезд.
Стоит заметить, что широкополосные ГВ-импульсы от двойных НЗ и систем БК+НЗ почти
ни чем не отличаются, за исключением их длительности.
<< 2. Стационарная функция распределения | Оглавление | 4. Обсуждение >>
|
Публикации с ключевыми словами:
двойные звезды - гравитационное излучение
Публикации со словами: двойные звезды - гравитационное излучение | |
См. также:
Все публикации на ту же тему >> | |