Физический вакуум и космическая анти-гравитация

---

<< 3. Физический вакуум и ... | Оглавление | 5. Статический мир >>

4. Анти-гравитация и ускоряющееся расширение

В статье Я.Б. Зельдовича [17], опубликованной в уже упоминавшемся фридмановском выпуске Успехов Физических Наук за 1963 г. (тогда отмечалось сороколетие теории расширяющейся Вселенной), обьясняется, как динамику космологического расширения можно наглядно представить на языке ньютоновской механики. Существует способ рассуждений, впервые предложенный Е.А. Милном и У.Г. МакКри в начале 1930-х годов, который позволяет избежать всех (точнее, почти всех) парадоксов ньютоновского тяготения, которые возникают при попытке применить классическую механику к неограниченному, бесконечному в пространстве распределению тяготеющей массы; при этом удается получить результат, который в точности совпадает с тем, что дает релятивистская теория Фридмана. Оказывается, что о бесконечности можно забыть, если рассмотреть шар конечных размеров, мысленно выделенный из общего однородного распределения вещества. На динамику шара внешние слои вещества не влияют, так как они сферически-симметричны, а внутренняя масса шара действует на точку на его поверхности так, как если бы вся эта масса была сосредоточена в центре шара. Тогда закон обратных квадратов дает уравнение движения для частицы на поверхности шара:

Здесь - радиус шара, - его полная гравитирующая масса:

Воспользуемся этим приемом чтобы показать роль вакуума в динамике космологического расширения. Если в полную гравитирующую плотность шара включить плотности всех четырех названных выше компонент космической среды, то получим

где гравитационный эффект давления (который отсутствует в ньютоновском тяготении, но должет быть, конечно, принят во внимание в нашем рассмотрении) учтен как для вакуума, так и для излучения с его уравнением состояния .

В космологической модели Эйнштейна имеется только вакуум и нерелятивистское вещество с плотностью ; поэтому в такой модели . Мир Эйнштейна статичен, так как эффективная гравитирующая плотность считается в этой модели равной нулю. Из условия вытекает связь между плотностями, , что и описывает баланс гравитации вещества и анти-гравитации вакуума. В этом случае сила и ускорение в уравнении движения (6) для шара равны нулю, и для неизменности его радиуса остается только потребовать, чтобы и скорость частиц шара равнялась нулю. В модели Фридмана эти условия необязательны; отсюда - возможность динамики и эволюции, шар может, вообще говоря, сжиматься или расширяться.

При адиабатическом сжатии или расширении однородного шара связь между изменением плотности и давлением описывается уравнением

для любой компоненты среды, если между компонентами нет обмена энергией. Как легко проверить, это соотношение вытекает из термодинамического тождества (где, как обычно, - полная внутреняя энергия (считая с энергией покоя), температура вещества и его энтропия в объеме ), если считать, что . Из уравнения (9) легко найти, как плотности вещества и излучения изменяются со временем при изменении его радиуса в ходе расширения или сжатия шара:

Здесь три величины - произвольные постоянные интегрирования. То же термодинамическое уравнение (9) лишний раз указывет, что вакуум при его уравнении состояния должен иметь постоянную во времени плотность: .

Если подставить соотношения (8,10) в уравнение движения (6), то последнее можно один раз проинтегрировать по времени:

Здесь - произвольная константа интегрирования; точнее, это величина не зависит от времени, но является функцией полной массы шара. Радиус шара и сам, очевидно, зависит от массы шара; радиус играет роль эйлеровой координаты для частицы, находящейся на поверхности шара, а масса барионов шара, которая не меняется со временем для данной частицы, служит ее лагранжевой координатой. Входящие в последнее соотношение константы даются общим соотношением

в котором для каждой компоненты космической среды. Для вакуума , для темного вещества и барионов , для излучения ; . Если для какого-то значения известны соответствующие значения плотностей, константы могут быть найдены. Эти интегралы служат, таким образом, для задания начальных условий в теории Фридмана. Как видно из (12), интегралы для разных уравнений состояния имеют одинаковую размерность (длины). Их численные значения близки друг к другу по порядку величины и составляют см (см. далее).

Интеграл для вещества без давления появился (и был обозначен таким образом) в первой космологической работе Фридмана [5] - см. формулу (8) этой классической статьи. Будем называть интегралы (12) для различных форм космической энергии фридмановскими интегралами.

Как всегда, первый интеграл уравнений движения есть энергия, и величина в (11) - это полная механическая энергия частицы в расчете на единицу массы. Кинетическая энергия стоит в левой части уравнения (12), а потенциальная энергия (обе эти энергии тоже относятся к единичной массе) - это взятая с противоположным знаком сумма первых четырех слагаемых в правой части этого уравнения. Полная энергия может быть положительной, отрицательной или равной нулю; соответствующие типы движения обычно называют гиперболическим, эллиптическим и параболическим.

Замечательно, что во фридмановский космологии динамика расширяющейся Вселенной дается уравнением точно того же вида, что и ньютоновский закон сохранения энергии (11):

В теории Фридмана - масштабный фактор, пропорционально которому изменяются все расстояния в расширяющемся мире; для моделей ненулевой пространственной кривизны эта величина служит и радиусом кривизны трехмерного пространства. Знак кривизны в (13), (для закрытой, плоской и открытой моделей, соответственно), противоположен знаку полной энергии в ньютоновском аналоге фридмановского уравнения. Имеется, таким образом, взаимно-одназначная связь между кривизной пространства и динамическим типом космологического расширения.

Точное подобие релятивистского и ньютоновского уравнений не простая случайность; это очевидное проявление в данном случае одного из основных принципов теоретической физики, принципа соответствия, согласно которому новая более общая теория включает в себя в качестве предельного или частного случая старую теорию в области ее применимости. Можно считать, что ньютоновские уравнения для однородного шара применяются при условии, что скорость расширения шара гораздо меньше скорости света, а гравитационный потенциал на поверхности шара гораздо меньше скорости света в квадрате. Эти условия определенно выполняются для шара достаточно малого радиуса. Но в мире Фридмана все расстояния, считая и малые, изменяются пропорционально масштабному фактору ; следовательно и для малого шара . Отсюда и вытекает необходимость точного подобия уравнений для и для как функции времени. Далее в формулах (9)-(11) будем подразумевать под стоящем там .

(Стоит заметить, что при ньютоновском описании космологического расширения без парадоксов все же не обходится. Действительно, уравнение движения (6) записано, как нужно считать, в инерциальной системе отсчета. В этой системе частица, находящаяся в центре рассматриваемого шара, покоится; с нею связано начало координат. Но в однородном мире все без исключения частицы равноправны, и значит, точно такое же уравнение движения можно записать и в системе отсчета, связанной с частицей, которая находится, например, на поверхности того же шара. Однако частица на поверхности шара движется относительно его центра отнюдь не равномерно, а согласно уравнению (6), с отличным от нуля ускорением. Поэтому обе системы отсчета не могут быть одновременно инерциальными. Этот парадокс снимается в общей теории относительности, где равноправны все свободно падающие системы отсчета, т.е. системы отсчета, которые опираются на физические тела, беспрепятственно движущиеся в поле тяжести.)

Из уравнений (11,13) можно видеть, что динамическая роль вакуума различна на разных этапах космологического расширения. На ранних этапах, при малых или (формально при ) слагаемое в правой части обоих уравнений, которое описывает вакуум, должно быть меньше четырех других слагаемых ( ). Значит, на этих этапах расширения влияние вакуума несущественно. В таком случае можно проинтегрировать уравнения (11,13) в пренебрежении вакуумом (см., например, [18]) и тем самым найти решение задачи при условии динамического доминирования обычного вещества и излучения. Так как тяготение обычного вещества и излучения создает отрицательное ускорение, , космологическое расширение происходит с замедлением на этих ранних этапах эволюции мира.

При больших временах роль вакуума становится существенной, и, как следует из уравнений (11,13), рано или поздно наступает этап динамического преобладания вакуума, когда вакуумное слагаемое в правой части этих уравнений оказывается много больше трех других слагаемых справа, описывающих не-вакуумные компоненты космической среды. В этом предельном случае больших времен (формально при ) тяготением не-вакуумных компонент можно пренебречь, и решение уравнений (11,13) имеет вид:

для , соответственно. Здесь, как и выше, см есть фридмановский интеграл для вакуума, получающийся из общего соотношения (12) при . Интеграл оказывается постоянным коэффициентом решений для ; естественно также выбрать его и для нормировки масштабного фактора при .

Так как вакуум с положительной плотностью создает эффективную анти-гравитацию (его эффективная гравитирующая плотность , как мы уже не раз говорили), ускорение оказывается положительным, когда в динамике расширения доминирует вакуум, и решение (14) описывает космологическое расширение, которое ускоряется со временем. Для всех трех вариантов модели Фридмана, отвечающих трем типам динамики, космологическое расширение продолжается, согласно (14), неограниченно долго. В пределе больших времен расширение происходит по экспоненциальному закону для всех трех вариантов.

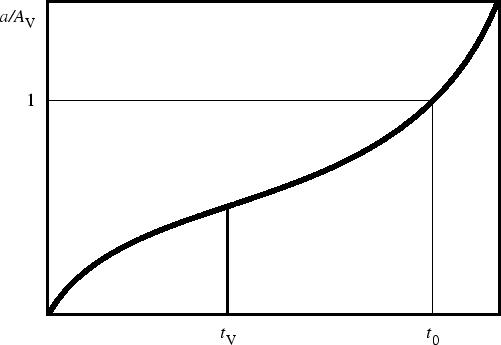
Смена замедления ускорением и переход к доминированию вакуума в динамике космологического расширения соответствует равенству плотностей , которое имеет, очевидно, тот же смысл, что и в статической модели Эйнштейна. Но в модели Фридмана это равенство возможно только в один момент времени, и в этот единственный момент ускорение обращается в нуль. Соответствующее красное смещение

Здесь - современный возраст мира; численное значение красного смещения дано для наблюдаемых плотностей (2-5).

Как мы говорили, эффект космологического ускорения, открытый в наблюдениях сверхновых, проявляется в зависимости их блеска от красного смещения для больших красных смещений, - больших, но не превышающих , как и должно быть, поскольку в более ранние времена расширение не ускорялось, а еще замедлялось.

В космологическом решении (14) хаббловская постоянная есть , практически для любого вскоре после перехода к доминированию вакуума. На стадии полного преобладния вакуума постоянная Хаббла не зависит от времени и определяется только значением плотности космического вакуума. Легко проверить, что эта связь постоянной Хаббла и плотности вакуума согласуется с измеренными значениями этих величин (в пределах ошибки измерений), - см. данные, приведенные в п.2. Существенно, что речь здесь идет о двух независимых типах космологических измерений.

Остается теперь записать решение фридмановского космологического уравнения (13) для всех времен:

Здесь принят знак плюс перед корнем квадратным, так как рассматривается расширение, а не сжатие космической среды; в качестве начала отсчета времени принят момент, когда . Решение (16) представлено графически на Рис.1, построенном в соответствии с данными о постоянной Хаббла и о плотностях вакуума, темного вещества, барионов и излучения, приведенными в (2-5). Космологическое расширение становится ускоряющимся при млрд лет; современный возраст мира млрд лет. В современную эпоху см. Последнее приближенное соотношение означает совпадение растущей со временем величины с постоянной длиной ; это одно из космических совпадений, характеризующих современную эпоху, и как будет показано далее, оно существенно также для понимания других космических совпадений.

Интересно, что в обоих предельных случаях, при и при , динамика космологического расширения не зависит от знака полной энергии или знака пространственной кривизны , как это видно из уравнения (16). Для всех трех вариантов динамики и кривизны расширение начинается в параболическом режиме; затем в течение конечного времени может проявиться возможное отличие динамики расширения от этого режима, а после этого расширение вновь выходит на параболический режим и сохраняет этот тип движения неограниченно долго.

Легко видеть, что возможные отличия от параболичности в действительности невелики при значениях плотностей (2)-(5). В соответствии с фридмановской теорией, последнее означает, что отклонения от плоской геометрии 3-пространства тоже не могут быть большими в реальном мире. Тем самым в обновленной стандартной космологии сама собой решается так наз. проблема плоскостности, которую еще недавно рассматривали как серьезную трудность этой науки.

---

<< 3. Физический вакуум и ... | Оглавление | 5. Статический мир >>

Публикации с ключевыми словами: Космология - космомикрофизика - вакуум - Расширение Вселенной - квантовая гравитация - антигравитация - лямбда-член - Общая теория относительности Публикации со словами: Космология - космомикрофизика - вакуум - Расширение Вселенной - квантовая гравитация - антигравитация - лямбда-член - Общая теория относительности
См. также: Разложение далекого света Формирование галактик в магнитной Вселенной "Эффекты" Зельдовича, запечатлённые на нашем небе Сверхновая 1994D и неожиданная Вселенная Куда смещается красное смещение? Не боги расширение вселенной наблюдают Самая далекая сверхновая типа Ia Все публикации на ту же тему >>