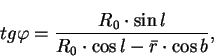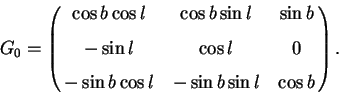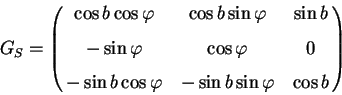Определение кривой вращения и шкалы расстояний в Галактике
<< 2. Расстояния до объектов
| Оглавление |
4. Кинематическая модель: движение >>
3. Системы координат
Рис. 1.
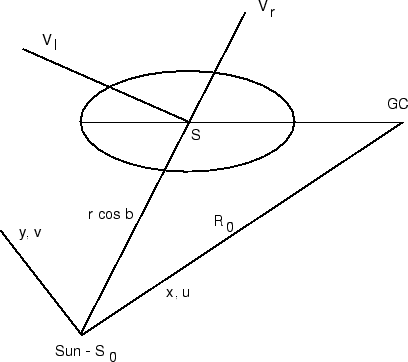 |
На рисунке схематически показан треугольник "Солнце (центроид
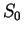
) - центр Галактики (GC) - исследуемый центроид
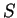
",
спроектированный на плоскость симметрии Галактики, а также
связанный с центроидом эллипсоид скоростей. Будем считать, что
его малая ось параллельна оси вращения Галактики, а большая ось
указывает на ее центр. Галактическая долгота
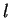
равна углу
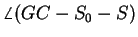
. Показаны также положительные направления
лучевой скорости и тангенциальной скорости по галактической
долготе. Мы будем использовать три системы координат:
галактическую прямоугольную систему координат, оси которой
параллельны основным галактическим направлениям; так наз.
локальную систему координат, связанную с направлением на
исследуемый центроид; а также систему координат, связанную с
главными осями эллипсоида скоростей текущего центроида
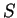
(см.
рис.
1). Орты галактической прямоугольной системы координат
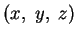
и соответствующие им компоненты скорости
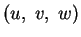
направлены на центр Галактики (
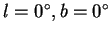
), в
сторону галактического вращения (
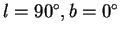
) и к
северному полюсу Галактики (
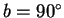
) и образуют правую
тройку. Орты локальной системы координат (в которой мы будем
записывать выражения для наблюдаемых компонентов скоростей
объекта) направлены соответственно на объект, в сторону увеличения
галактических долгот (параллельно плоскости симметрии Галактики)
и в сторону увеличения галактических широт, и также образуют
правую тройку. Пусть
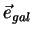
- единичный вектор-столбец
в прямоугольной галактической системе координат, а
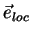
- тот же вектор в локальной системе координат.
Они связаны преобразованием поворота
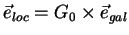
, где матрица
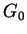
равна
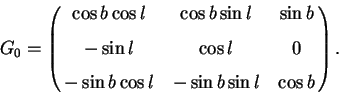 |
(1) |
Аналогичным образом матрица
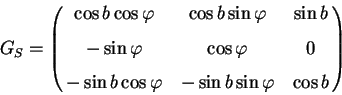 |
(2) |
выполняет преобразование поворота из системы координат, связанной
с осями эллипсоида скоростей
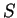
, в локальную систему координат
(см. рис.
1). При этом вспомогательный угол
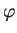
, определяющий
ориентацию эллипсоида скоростей в области центроида
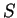
(равный
углу между проекцией луча зрения на галактическую плоскость и
большой осью эллипсоида скоростей) и играющий роль галактической
долготы в (
1), вычисляется по формуле
с учетом того, что угол
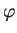
меняется в интервале
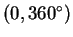
. Здесь и далее
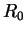
- расстояние от Солнца до
центра Галактики. В этом выражении в качестве гелиоцентрического
расстояния взято уточненное расстояние
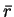
.
<< 2. Расстояния до объектов
| Оглавление |
4. Кинематическая модель: движение >>