Астронет > 2.3 Обобщенная процедура Белинфанте. Независимость обобщенных законов сохранения от дивергенций в лагранжианах

по текстам по ключевым словам в глоссарии по сайтам перевод по каталогу

<< 2.2 Приложение процедуры Белинфанте ... | Оглавление | Литература к Лекции 2 >>

2.3 Обобщенная процедура Белинфанте. Независимость обобщенных законов сохранения от дивергенций в лагранжианах

Напомним, что в лекции 1 процедура Нетер была приложена к общего вида теории с лагранжианом $\hat L = \hat L (A_B; A_{B,\alpha}; A_{B,\alpha\beta})$ , который был ,,ковариантизован'' введением внешней фоновой метрики $\bar g_{\mu\nu}$ и приведен к виду

$\begin{displaymath} \hat L = {\hat{\cal L}}_c = {{\hat{\cal L}}}_c (A_B; \overline D_\alpha A_{B}; \overline D_\beta \overline D_\alpha A_{B}). \end{displaymath}$

(2.30)

Был получен закон сохранения

$\begin{displaymath} \hat i^\alpha \equiv \overline D_\tau \hat \Phi^{\alpha\tau}(\xi) \end{displaymath}$

(2.31)

с током и суперпотенциалом определенными в лекции 1:

$\displaystyle \hat i^\alpha$	$\textstyle \equiv$	$\displaystyle -\left[\left(\hat u^{\alpha}_\sigma + \hat n^{\alpha\tau\beta}_\l... ...\alpha\tau}_{\sigma}\overline D_\tau \xi^\sigma + \hat Z^{\alpha}_{(1)}\right],$
$\displaystyle \hat \Phi^{\alpha\tau} (\xi)$	$\textstyle \equiv$	$\displaystyle \left(\hat m^{\tau\alpha}_\sigma + \overline D_\lambda \hat n^{\l... ...{4\over 3}} \hat n^{[\alpha\tau]\lambda}_\sigma \overline D_\lambda \xi^\sigma,$

коэффициенты в которых определены в формулах (39) - (41) лекции 1. Определяем поправку Белинфанте по стандартным правилам (2.17)

$\begin{displaymath} \hat S^{\mu\nu\rho} \equiv - \hat m^{\rho[\mu}_\lambda \bar ... ...{\nu]\lambda} + \hat m^{\nu[\rho}_\lambda \bar g^{\mu]\lambda} \end{displaymath}$

(2.32)

и добавляем к обеим частям 2.31) величину $\overline D_\tau \left(\hat S^{\alpha\tau\rho}\xi_{\rho}\right)$ . Получим обобщенный закон сохранения, соответствующий комбинации процедур Нетер и Белинфанте:

$\begin{displaymath} \hat i^\alpha_{NB} \equiv \overline D_\tau \hat \Phi^{\alpha\tau}_{NB}(\xi). \end{displaymath}$

(2.33)

Теперь скорректированный ток приобретает вид:

$\begin{displaymath} \hat i^\alpha_{NB} \equiv -\left[ \left(\hat u^{\alpha}_\sig... ...}_{ \sigma}\right) \xi^\sigma+ \hat Z^{\alpha}_{(2)}\right], \end{displaymath}$

(2.34)

а скорректированный суперпотенциал:

$\begin{displaymath} \hat \Phi^{\alpha\tau}_{NB} (\xi) \equiv 2\left[\overline D_... ...t n^{[\alpha\tau]\lambda}_\sigma\overline D_\lambda\xi^\sigma. \end{displaymath}$

(2.35)

2.3.1 Свойства новых законов сохранения и новых скорректированных величин

(a) Как и должно быть в силу определения процедуры Белинфанте, ток (2.34) не содержит явно спинового члена. Законы сохранения теперь определяются единым обощенным ,,симметризованным'' тензором энергии-импульса


		$\displaystyle \hat {\cal T}_{(NB)\sigma}^\alpha = - \left(\hat u^{\alpha}_\sigm... ...mbda_{ \tau\beta\sigma} - \overline D_\nu \hat S^{\alpha\nu}_{ \sigma}\right).$

Z-член, как и прежде, обращается в нуль на киллинговых векторах фона.

(b) В вопросе об единственности все те утверждения, которые были сделаны относительно обобщенных токов и суперпотенциалов $\hat i^\alpha$ and $\hat \Phi^{\alpha\tau}$ в лекции 1 остаются в силе. Поправка Белинфанте (2.32) также определена однозначно лагранжианом (2.30).

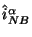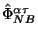Таким образом, мы утверждаем, что $\hat i^\alpha_{NB}$ и $\hat \Phi^{\alpha\tau}_{NB}$ единственным образом в смысле процедуры Нетер-Белинфанте определяются лагранжианом модели.

Этот вывод важен для нас по следующей причине. Подстановка в формулы (2.32) - (2.35) конкретного лагранжиана КБЛ ( ${\hat{\cal L}}_G$ в (2.20)) дает точно те результаты, которые предложены в предыдущей части. А это означает, что пункт (ii) в прошлой части этой лекции подтверждается, то есть результаты [10] $^{\!- }$ [12], однозначны в смысле процедуры Нетер-Белинфанте.

(c) Заметим, что суперпотенциал (2.35) зависит только от n-коэффициентов. Это хорошо соотносится с известными фактами. Например, более простая теория с лагранжианом (2.9) не содержит n-коэффициентов -- результат такой, что после приложения метода Белинфанте скорретированный суперпотенциал в (2.18) обращается в нуль. В более сложной модели Моллера [16], где ОТО представлена с помощью тетрад, но без вторых производных в ковариантном лагранжиане, также отсутствуют n-коэффициенты. Результат тот же: Белинфанте поправка дает нулевой суперпотенциал. В этом смысле модель с КБЛ лагранжианом более предпочтительна: она приводит к суперпотенциалу типа (2.35), который приводит к законам сохранения удовлетворяющим всем естественным тестам.

2.3.2 Независимость от дивергенций в лагранжиане

Напомним, что вклады в ток и суперпотенциал (полученные методом Нетер) от дивергенции в лагранжиане: $\Delta_{(div)} \hat L = \partial_\nu \hat k^\nu$ соответствуют формулам:

		$\displaystyle \hat i^\alpha +\Delta_{(div)} \hat i^\alpha$
		$\displaystyle = - \left(\hat u^{\alpha}_\sigma + \Delta_{(div)} \hat u^{\alpha}... ...^{\alpha\tau}_{\sigma}\right) \overline D_\tau \xi^\sigma - \hat Z^\alpha_{(1)}$
		$\displaystyle \equiv \overline D_\tau \left[\hat \Phi^{\alpha\tau} + \Delta_{(div)} \hat \Phi^{\alpha\tau}(\xi)\right],$	(2.36)

где

$\displaystyle \Delta_{(div)}\hat u^\alpha_\sigma$	=	$\displaystyle 2 \overline D_\tau\left(\delta^{[\alpha}_\sigma \hat k^{\tau]} \right),$
$\displaystyle \Delta_{(div)}\hat m^{\alpha\tau}_\sigma$	=	$\displaystyle 2 \left(\delta^{[\alpha}_\sigma \hat k^{\tau]} \right),$
$\displaystyle \Delta_{(div)}\hat \Phi^{\alpha\tau}$	=	$\displaystyle -2 \left(\xi^{[\alpha} \hat k^{\tau]} \right).$	(2.37)

Поправка Белинфанте (2.32) для добавки $\Delta_{(div)} \hat m^{\alpha\tau}_{\sigma}$ имеет также простую форму:

$\begin{displaymath} \Delta_{(div)} \hat S^{\alpha\tau\rho}\xi_\rho = 2\xi^{[\alpha}\hat k^{\tau]}. \end{displaymath}$

(2.38)

Применим Белинфанте метод к (2.36). В силу определения процедуры исчезнет спиновый член. А в силу значений (2.37) и (2.38) исчезнут и совместные поправки:

$\Delta_{(div)} \hat u^{\alpha}_\sigma - \overline D_\tau \left(\Delta_{(div)} \hat S^{\alpha\tau\rho}\bar g_{\rho\sigma}\right)\equiv 0,$

$\Delta_{(div)} \hat S^{\alpha\tau\rho}\xi_\rho + \Delta_{(div)} \hat \Phi^{\alpha\tau}\equiv 0$ .

Таким образом, комбинированная процедура Нетер-Белинфанте приводит к дивегентно независимым величинам в законах сохранения. Иначе, форма сохраняющихся тока и суперпотенциала не зависят от граничных условий при варьировании лагранжиана.

Этот результат подтверждает пункт (ix) прошлой части этой лекции. В работе [17] уже было отмечено, что метод Белинфанте, примененный как к усеченному лагранжиану Эйнштейна, так и лагранжиану Гилберта дает один и тот же результат. Фактически мы обобщаем этот результат на произвольные теории с произвольно искривленными фонами. Результаты этой части доложены на семинаре [18].

<< 2.2 Приложение процедуры Белинфанте ... | Оглавление | Литература к Лекции 2 >>

Публикации с ключевыми словами: законы сохранения - Общая теория относительности - гравитация
Публикации со словами: законы сохранения - Общая теория относительности - гравитация

См. также:

Падение шара в Солнечной системе

Гравитационные аномалии на Меркурии

Галактика Арп 94

Спутники GRAIL составляют карту лунной гравитации

70 лет Стивену Хокингу

Молоток против пёрышка на Луне

Спутник Gravity Probe B подтвердил наличие гравимагнетизма

Все публикации на ту же тему >>

Обсудить эту публикацию

Версия для печати

Астрометрия - Астрономические инструменты - Астрономическое образование - Астрофизика - История астрономии - Космонавтика, исследование космоса - Любительская астрономия - Планеты и Солнечная система - Солнце