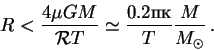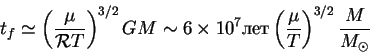<< 5.2 Образование звезд. | Оглавление | 5.4 Стационарные звезды >>
5.3 Протозвезды.
Качественно проследим, как происходит коллапс молекулярного
облака, размер которого удовлетворяет критерию неустойчивости Джинса.
Рассмотрим сферическое облако идеального газа
с массой ![]() . Оно будет сжиматься из-за самогравитации, если
радиус удовлетворяет неравенству
. Оно будет сжиматься из-за самогравитации, если
радиус удовлетворяет неравенству
Облако начинает сжиматься в шкале свободного падения
![]() ,
поскольку хорошая прозрачность нейтрального вещества
для фотонов позволяет сжатию происходить практически в изотермическом
режиме.
Подставляя радиус из (5.1), находим время свободного сжатия
как функцию температуры:
,
поскольку хорошая прозрачность нейтрального вещества
для фотонов позволяет сжатию происходить практически в изотермическом
режиме.
Подставляя радиус из (5.1), находим время свободного сжатия
как функцию температуры:
Энергия, выделяемая при гравитацинном сжатии, ведет к увеличению
температуры. Пока вещество не является плазмой, его непрозрачность мала,
и рождающиеся фотоны низких энергий
свободно выходят из облака, унося часть выделяемой энергии.
По мере роста плотности время свободного падения укорачивается,
но рост плотности ведет к росту непрозрачности (в основном
из-за поглощения ИК-фотонов пылью и молекулами)
поэтому изотермическое сжатие постепенно сменяется на
адиабатическое.
Легко можно оценить радиус,
до которого может сжаться облако с данной массой, из условия затраты
выделяемой гравитационной энергии на диссоциацию молекул и ионизацию
вещества. Пусть вещество изначально состоит из молекулярного водорода.
На диссоциацию одной молекулы ![]() затрачивается
затрачивается
![]() эрг,
на ионизацию каждого атома водорода требуется еще 13.6 эВ (
эрг,
на ионизацию каждого атома водорода требуется еще 13.6 эВ (
![]() эрг), то есть для превращения
1 г вещества в плазму нужно затратить
эрг), то есть для превращения
1 г вещества в плазму нужно затратить
![]() эрг. Присутствие молекул гелия повышает эту оценку
почти в 2 раза. Из условия
эрг. Присутствие молекул гелия повышает эту оценку
почти в 2 раза. Из условия
![]() находим радиус "непрозрачной" протозвезды
находим радиус "непрозрачной" протозвезды
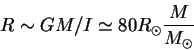
Заметим, что в процессах диссоциации и ионизации энергия затрачивается на разрыв молекулярных связей или отрыв электронов от атомов (фазовый переход 1 рода), а значит при адиабатическом сжатии рост температуры при прочих равных условиях будет меньше. Это означает, что показатель адиабаты
Можно оценить и светимость протозвезды на стадии сжатия
в шкале свободного падения.
Поскольку источником энергии служит гравитационная энергия сжимающегося
облака, то
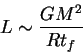
Подставляя (5.1), (5.2) получаем
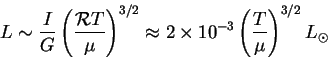
(
Дальнейшее сжатие собственно непрозрачной (т.е. имеющей фотосферу, как
и Солнце) протозвезды происходит также в динамической шкале времени.
Светимость протозвезды на непрозрачной стадии определяется балансом
выделяемой
гравитационной энергии и способностью высвечивания энергии с поверхности,
которая, как известно, максимальна для абсолютно
черного тела
![]() , где
, где ![]() - эффективная
температура. Температура фотосферы звезды определяется условием
просачивания квантов из толщи звезды наружу, т.е. непрозрачностью звездных
недр. Расчеты показывают, что у протозвезд энергия переносится
конвективными движениями в оболочке (возникновение конвекции
связано с увеличением непрозрачности с ростом плотности в условиях
ионизации водорода и гелия), при этом в фотосфере устанавливается
универсальная температура порядка 3500 K. На диаграмме Герцшпрунга-Рессела
звезда эволюционирует вдоль т.н. конвективного трека Хаяши,
который впервые количественно
рассчитал это процесс, и сама стадия сжимающейся
конвективной протозвезды носит название стадии Хаяши.
- эффективная
температура. Температура фотосферы звезды определяется условием
просачивания квантов из толщи звезды наружу, т.е. непрозрачностью звездных
недр. Расчеты показывают, что у протозвезд энергия переносится
конвективными движениями в оболочке (возникновение конвекции
связано с увеличением непрозрачности с ростом плотности в условиях
ионизации водорода и гелия), при этом в фотосфере устанавливается
универсальная температура порядка 3500 K. На диаграмме Герцшпрунга-Рессела
звезда эволюционирует вдоль т.н. конвективного трека Хаяши,
который впервые количественно
рассчитал это процесс, и сама стадия сжимающейся
конвективной протозвезды носит название стадии Хаяши.
Светимость протозвезды на стадии Хаяши есть просто
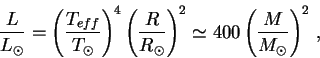
а время жизни определяется из условия
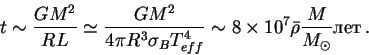
Как только температура и плотность в центре звезды достаточно возрастут, начнутся ядерные реакции и протозвезда станет нормальной звездой, находящейся на главной поледовательности диаграммы Герцшпрунга - Рассела.
Разумеется, реальная картина сжатия протозвезд существенно сложнее. В частности, мы пренебрегали эффектами магнитного поля и вращения, которые неизбежно присутствуют в астрофизических условиях. Оба эффекта препятствуют сжатию протозвезд.
Роль вращения достаточно очевидна. Из закона
сохранения момента импульса облака с заданной массой ![]() при сжатии
при сжатии
![]() следует, что
энергия вращения при сжатии возрастает как
следует, что
энергия вращения при сжатии возрастает как
![]() . Рост гравитационной
энергии происходит медленнее,
. Рост гравитационной
энергии происходит медленнее,
![]() ,
а значит при некотором радиусе центробежные силы остановят сжатие.
,
а значит при некотором радиусе центробежные силы остановят сжатие.
Менее очевидно влияние магнитного поля. В холодных молекулярных
облаках поле "взаимодействует" с нейтральными частицами
посредством физического процесса, аналогичного амбиполярной
диффузии в лабораторной плазме. В отличии от последнего случая
(диффузия легких электронов приводит к диффузии тяжелых ионов
из-за Кулоновского взаимодействия), в межзвездной среде
с магнитным полем взаимодействуют тяжелые ионы, а связь
с нейтральными атомами осуществляется через столкновения
атомов с ионами.
Характерное время диффузии неоднородного
магнитного поля из межзвездного облака за счет этого процесса
оказывается порядка
где
<< 5.2 Образование звезд. | Оглавление | 5.4 Стационарные звезды >>
|
Публикации с ключевыми словами:
звезды - Межзвездная среда - Космология - теоретическая астрофизика - астрофизика
Публикации со словами: звезды - Межзвездная среда - Космология - теоретическая астрофизика - астрофизика | |
См. также:
Все публикации на ту же тему >> | |