<< 3.3 Астрономическое intermezzo: Звездные | Оглавление | 3.5 О точности измерений >>
- 3.4.1 Когерентность света
- 3.4.2 Спекл-интерферометрия
- 3.4.3 Адаптивная оптика
- 3.4.4 Статистика фотонов. Дробовой и волновой шум.
3.4 Физические ограничения на точность астрономических наблюдений
3.4.1 Когерентность света
Звезды - не точки с бесконечно малыми угловыми размерами,
а имеют конечный (хотя и очень малый)
угловой размер. Например, диск Солнца с радиусом видимой
фотосферы
![]() см с расстояния 10 пк
виден под углом
см с расстояния 10 пк
виден под углом
![]() . Поскольку
наблюдения проводятся телескопами (приемниками) с конечной апертурой
(диаметром)
. Поскольку
наблюдения проводятся телескопами (приемниками) с конечной апертурой
(диаметром) ![]() , нужно учитывать дифракцию Френеля: для
монохроматичекого источника с длиной волны
, нужно учитывать дифракцию Френеля: для
монохроматичекого источника с длиной волны ![]() размер дифракционного
кружка изображения
размер дифракционного
кружка изображения
![]() .
.
ЗАМЕЧАНИЕ: Атмосферная турбулентность искажает фронт световой волны,
размывая точечное изображение до размеров порядка 1", что намного больше
диаметра дифракционного кружка. Довольно редко на высокогорных обсерваториях
достигается "качество изображения" ![]() (напрмер, в обсерватории
Мауна Кеа (4000 м над у.м.) на Гавайских островах, в Европейской Южной
Обсерватории в Чили, на горной обсерватории Майданак в Узбекистане).
Космические телескопы, разумеется, свободны от влияния атмосферы, и там
достигается дифракционный предел углового разрешения.
(напрмер, в обсерватории
Мауна Кеа (4000 м над у.м.) на Гавайских островах, в Европейской Южной
Обсерватории в Чили, на горной обсерватории Майданак в Узбекистане).
Космические телескопы, разумеется, свободны от влияния атмосферы, и там
достигается дифракционный предел углового разрешения.
Если источник не точечный и имеет конечный угловой размер ![]() , то при
, то при
![]() источник должен рассматриваться как когерентный, т.к.
разница в длине пути лучей с разных "краев" источника меньше половины длины
волны (пример - звезда Вега:
источник должен рассматриваться как когерентный, т.к.
разница в длине пути лучей с разных "краев" источника меньше половины длины
волны (пример - звезда Вега:
![]() , пусть
, пусть ![]() м,
м,
![]() A, тогда
A, тогда
![]() ,
т.е. любое отклонение волнового фронта в пределах угла
,
т.е. любое отклонение волнового фронта в пределах угла ![]() оставляет
изображение когерентным (разность фаз не превышает
оставляет
изображение когерентным (разность фаз не превышает ![]() ). Таким образом,
из-за случайных искажений волнового фронта от источника с угловым размером
). Таким образом,
из-за случайных искажений волнового фронта от источника с угловым размером
![]() будет наблюдаться интерференционная картина до тех пор, пока
будет наблюдаться интерференционная картина до тех пор, пока
![]() . На этом принципе основаны звездные
интерферометры Майкельсона, с помощью которых измерили диаметры некоторых
близких звезд-гигантов еще в 1920-х гг.
Основная проблема этого метода - размытие интерференционной картины атмосферной
турбулентностью.
. На этом принципе основаны звездные
интерферометры Майкельсона, с помощью которых измерили диаметры некоторых
близких звезд-гигантов еще в 1920-х гг.
Основная проблема этого метода - размытие интерференционной картины атмосферной
турбулентностью.
Реальные источники, как правило, не монохроматические. Для них важно понятие
длины (области) когерентности. Из оптики известно, что по мере
увеличения разности хода контраст интерференционных полос уменьшается.
Разность хода записывается в виде
![]() , где
, где ![]() - время
когерентности. Для источника с полосой частот
- время
когерентности. Для источника с полосой частот ![]() , время
когерентности есть просто
, время
когерентности есть просто
![]() , где
, где ![]() - скорость света.
Физический смысл длины
когерентности прост. Это предельно допустимая разность хода для видности
интерференционных полос. В зависимости от соотношения апертура -
длина когерентности в различных диапазонах различают когерентный и
некогерентный прием сигнала.
- скорость света.
Физический смысл длины
когерентности прост. Это предельно допустимая разность хода для видности
интерференционных полос. В зависимости от соотношения апертура -
длина когерентности в различных диапазонах различают когерентный и
некогерентный прием сигнала.
Рассмотрим к примеру оптический диапазон,
![]() A,
A,
![]() А, тогда
А, тогда
![]() см и составляет
см и составляет ![]() несколько длин волн.
Наоборот, в радиодиапазоне,
где используются узкополосные детекторы (
несколько длин волн.
Наоборот, в радиодиапазоне,
где используются узкополосные детекторы (![]() см,
см,
![]() МГц длина когерентности
МГц длина когерентности
![]() см и составляет
см и составляет ![]() несколько
сотен длин волн. Тем самым в длинноволновом диапазоне может осуществляться
когерентный прием сигнала и достигаться очень высокие угловые разрешения
(радиоинтерферометрия). В оптике и более жестком диапазоне прием практически
всегда некогерентный. Несмотря на это можно делать оптическую
интерферометрию, используя идею метода апертурного синтеза (см. выше). Для
этого требуется по крайней мере два телескопа на расстоянии
несколько
сотен длин волн. Тем самым в длинноволновом диапазоне может осуществляться
когерентный прием сигнала и достигаться очень высокие угловые разрешения
(радиоинтерферометрия). В оптике и более жестком диапазоне прием практически
всегда некогерентный. Несмотря на это можно делать оптическую
интерферометрию, используя идею метода апертурного синтеза (см. выше). Для
этого требуется по крайней мере два телескопа на расстоянии ![]() друг от
друга и делаются короткие экспозиции (чтобы турбулетность атмосферы не
размыла интерфернционную картину) при различных ориентациях оси
телескоп-телескоп относительно источника (этому помогает суточное вращение
Земли). Полученная интерференционная картина в принципе может достигать
углового разрешения
друг от
друга и делаются короткие экспозиции (чтобы турбулетность атмосферы не
размыла интерфернционную картину) при различных ориентациях оси
телескоп-телескоп относительно источника (этому помогает суточное вращение
Земли). Полученная интерференционная картина в принципе может достигать
углового разрешения
![]() , для этого требуется сведение лучей от обеих телескопов
в едином фокусе с разностью хода, не превышающей длину когерентности.
Эта технически сложная задача будет реализована на 4-х телескопах VLT
Европейской Южной Обсерватории, и эквивалентный диаметр интерферометра
VLT будет равняться 16 м с угловым разрешением
, для этого требуется сведение лучей от обеих телескопов
в едином фокусе с разностью хода, не превышающей длину когерентности.
Эта технически сложная задача будет реализована на 4-х телескопах VLT
Европейской Южной Обсерватории, и эквивалентный диаметр интерферометра
VLT будет равняться 16 м с угловым разрешением ![]() на длине
волны 5000 А. В 2000 г. в вошел в строй второй из четырех
8.2-м телескопов VLT. К концу 2001 года были
получены первые интерферометричвеские наблюдения на
двух телескопах VLT, работающих в режиме интерферометра с базой 102 м.
Измерены угловые размеры нескольких звезд на уровне
одной миллисекунды дуги (рекорд наземных наблюдений).
К 2010 г. планируется запуск космического
интерферометра TPF (Terrestrial Planet Finder), состоящего из четырех 3.5-м
телескопов с максимальной базой 1 км. Угловой разрешение достигнет
на длине
волны 5000 А. В 2000 г. в вошел в строй второй из четырех
8.2-м телескопов VLT. К концу 2001 года были
получены первые интерферометричвеские наблюдения на
двух телескопах VLT, работающих в режиме интерферометра с базой 102 м.
Измерены угловые размеры нескольких звезд на уровне
одной миллисекунды дуги (рекорд наземных наблюдений).
К 2010 г. планируется запуск космического
интерферометра TPF (Terrestrial Planet Finder), состоящего из четырех 3.5-м
телескопов с максимальной базой 1 км. Угловой разрешение достигнет
![]() на длине волны 3 мкм и главная научная задача этого интерферометра
будет поиск планет земного типа вокруг ближайших звезд.
на длине волны 3 мкм и главная научная задача этого интерферометра
будет поиск планет земного типа вокруг ближайших звезд.
3.4.2 Спекл-интерферометрия
Как мы упоминали выше, атмосферная турбулентность искажает
волновой фронт и "размывает" изображение звезды. На Рис. 3.4
схематически показано прохождение волнового фронта через турбулентную
атмосферу. Для количественной характеристики масштаба турбулентности
в атмосфере вводится параметр ![]() (так называемый параметр Фрида). По физический смыслу он
эквивалентен диаметру телескопа, имеющего дифракционный предел
полуширины изображения
(так называемый параметр Фрида). По физический смыслу он
эквивалентен диаметру телескопа, имеющего дифракционный предел
полуширины изображения ![]() , которое соответствует
изображению, создаваемому атмосферой при наблюдении точечного источника
идеальным телескопом с бесконечным размером зеркала.
Параметр Фрида зависит от длины волны источника
, которое соответствует
изображению, создаваемому атмосферой при наблюдении точечного источника
идеальным телескопом с бесконечным размером зеркала.
Параметр Фрида зависит от длины волны источника
![]() и в оптическом диапазоне варьируется в пределах 5-20 см.
Чем больше параметр Фрида, тем более пригодно место для
астрономических наблюдений.
и в оптическом диапазоне варьируется в пределах 5-20 см.
Чем больше параметр Фрида, тем более пригодно место для
астрономических наблюдений.
Телескоп малых размеров ![]() строит дифракционное изображение
своей апертуры
строит дифракционное изображение
своей апертуры ![]() и практически не чувствует
атмосферное размытие изображения (левая часть рисунка).
Телескоп
большого диаметра
и практически не чувствует
атмосферное размытие изображения (левая часть рисунка).
Телескоп
большого диаметра ![]() (правая часть рисунка)
одновременно строит большое число отдельных дифракционных
изображений источника, которые "размываются" турбулентностью в
области с угловыми размерами
(правая часть рисунка)
одновременно строит большое число отдельных дифракционных
изображений источника, которые "размываются" турбулентностью в
области с угловыми размерами
![]() .
Таким образом при достаточно длинных экспозициях угловое разрешение
большого телескопа полностью определяется размером
создаваемого атмосферой изображения.
.
Таким образом при достаточно длинных экспозициях угловое разрешение
большого телескопа полностью определяется размером
создаваемого атмосферой изображения.
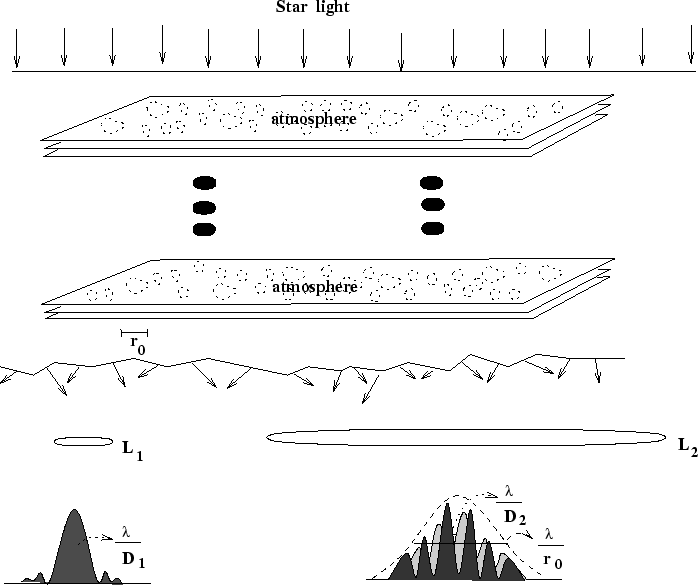 |
| Рис. 3.59
Прохождение света через турбулентную
атмосферу. Слева - регистрация телескопом малой апертуры
|
Разумеется, вынос телескопа за атмосферу (например, космический телескоп им.
Хаббла) снимает проблему
влияния атмосферы, но это весьма дорогостоящий способ
улучшения качества изображения.
В 1970-х гг. французский астроном
A.Labeyrie для увеличения углового разрешения больших наземных
телескопов предложил метод
спекл-интерферометрии3.4,
получивший широкое распространение.
Метод состоит в статистической обработке очень коротких экспозиций
(
![]() сек,
сек, ![]() - дисперсия
турбулентных скоростей),
за время которых дифракционное изображение не "размазывается" атмосферой
(ср. мерцание звезд!) (Рис. 3.5). На одной спеклограмме (верхняя
панель рисунка) отчетливо видны отдельные изображения двойной звезды
("спеклы"). Их число
- дисперсия
турбулентных скоростей),
за время которых дифракционное изображение не "размазывается" атмосферой
(ср. мерцание звезд!) (Рис. 3.5). На одной спеклограмме (верхняя
панель рисунка) отчетливо видны отдельные изображения двойной звезды
("спеклы"). Их число
![]() . Если сложить последовательные
спеклограммы (в среденй части рисунка сложены 128 спеклограмм),
увеличивая тем самым время экспозиции, то из-за случайности фаз
отдельных дифракционных изображений деструктивная интерференция
замоет картину (средняя часть рисунка). Однако простая математическая
обработка одной спеклограммы позволяет восстановить
исходную картину (нижняя часть рисунка). Например, в нижней части рисунка
приведена автокорреляционная функция верхней спеклограммы.
Отчетливо видна главная звезда (большой пик) с дифракционным
разрешением
. Если сложить последовательные
спеклограммы (в среденй части рисунка сложены 128 спеклограмм),
увеличивая тем самым время экспозиции, то из-за случайности фаз
отдельных дифракционных изображений деструктивная интерференция
замоет картину (средняя часть рисунка). Однако простая математическая
обработка одной спеклограммы позволяет восстановить
исходную картину (нижняя часть рисунка). Например, в нижней части рисунка
приведена автокорреляционная функция верхней спеклограммы.
Отчетливо видна главная звезда (большой пик) с дифракционным
разрешением ![]() и звезда-спутник меньшей интенсивности
(маленький пик справа и слева от большого; пики по краям картинки
являются артефактами процедуры обработки).
и звезда-спутник меньшей интенсивности
(маленький пик справа и слева от большого; пики по краям картинки
являются артефактами процедуры обработки).
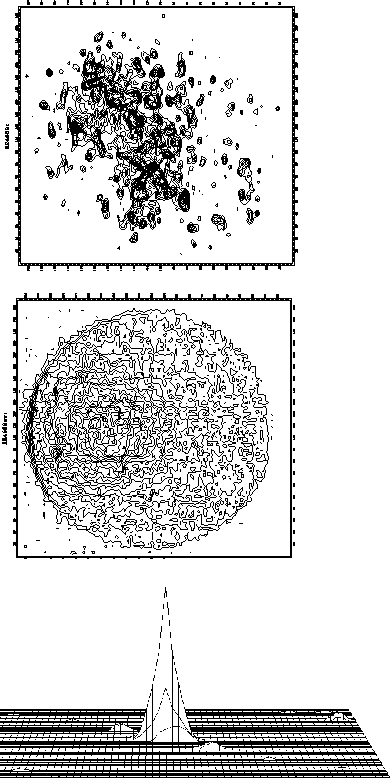 |
| Рис. 3.60 Спеклограмма двойной звезды (сверху), сумма 128 спеклограмм (середина) и автокорреляционная функция одной спеклограммы, на которой отчетливо водина двойственность источника. |
Для успешной спекл-интерферометрии существенны
два условия: 1) короткие экспозиции (![]() характерного времени
турбулентных дрожаний) и 2) достаточно узкая полоса приемника, чтобы быть
в зоне когерентности.
Интерференционная картина от источника конечных
угловых размеров будет видна, если
угловой размер его изображения
меньше отношения длины когерентности к диаметру телескопа.
характерного времени
турбулентных дрожаний) и 2) достаточно узкая полоса приемника, чтобы быть
в зоне когерентности.
Интерференционная картина от источника конечных
угловых размеров будет видна, если
угловой размер его изображения
меньше отношения длины когерентности к диаметру телескопа.
Пример: звезда с угловым диаметром
![]() ,
длина волны
,
длина волны
![]() A, телескоп
A, телескоп ![]() м, при этом
можно делать спекл-интерферометрию
(и например измерить угловой диаметр этой звезды или
угловое расстояние между двумя тесными звездами ) уже при
полосе приемника
м, при этом
можно делать спекл-интерферометрию
(и например измерить угловой диаметр этой звезды или
угловое расстояние между двумя тесными звездами ) уже при
полосе приемника
![]() A.
A.
3.4.3 Адаптивная оптика
Другой способ борьбы с атмосферной турбулентностью состоит
в использовании адаптивной оптики. Под адаптивной оптикой
понимают оптические устройства, которые механически изменяют
свои параметры таким образом, чтобы скомпенсировать искажения
волнового фронта, вызванные атмосферной
турбулентностью и иными причинами. В астрономических приборах
используют специальные деформируемые зеркала с диаметром
порядка 20 см, форма поверхности которых изменяется
в процессе экспозиции. Число сенсоров обратной связи, деформирующих
зеркало (т.н. активаторов), грубо говоря определяется из требования
(
Для контроля за формой волнового фронта используют
или яркую реперную звезду или (если рядом с наблюдаемым
объектом ярких звезд нет) "искусственную звезду", т.е.
кратковременную подсветку участка неба мощным лазерным
импульсом, настроенным на частоту резонансного перехода ![]() атома натрия. Свечение образуется на высотах порядка 90 км.
атома натрия. Свечение образуется на высотах порядка 90 км.
3.4.4 Статистика фотонов. Дробовой и волновой шум.
Рассмотрим стационарный источник света, принимаемый детектором поток
от которого в среднем составляет
![]() фот/сек (площадь детектора учтена).
В оптическом и более коротковолновом
диапазонах вероятность регистрации
фот/сек (площадь детектора учтена).
В оптическом и более коротковолновом
диапазонах вероятность регистрации ![]() квантов за время
квантов за время
![]() подчиняется с большой точностью статистике Пуассона
(см. исключения ниже)
подчиняется с большой точностью статистике Пуассона
(см. исключения ниже)
Следует заметить, что на самом деле статистика Пуассона хорошо соблюдается только в случае малого числа фотонов. В более общем случае приход фотонов описывается статистикой Пойа, для которой
где коэффициент
<< 3.3 Астрономическое intermezzo: Звездные | Оглавление | 3.5 О точности измерений >>
|
Публикации с ключевыми словами:
звезды - Межзвездная среда - Космология - теоретическая астрофизика - астрофизика
Публикации со словами: звезды - Межзвездная среда - Космология - теоретическая астрофизика - астрофизика | |
См. также:
Все публикации на ту же тему >> | |