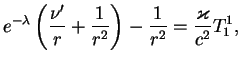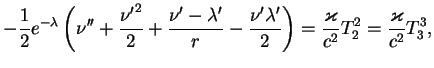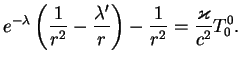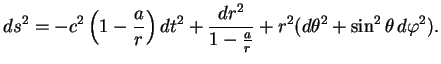Rambler's Top100Astronet    
  по текстам   по ключевым словам   в глоссарии   по сайтам   перевод   по каталогу 		 

На первую страницу
Физические основы строения и эволюции звезд
<< 8.4 Гравитационное красное смещение. | Оглавление | 9.2 Движение частиц в ... >>

9. Сильные гравитационные поля и строение релятивистских звезд


Разделы

9.1 Решение Шварцшильда

Рассмотрим сферически-симметричное и статическое решение уравнений Эйнштейна. Введем сферические координаты, записав выражение для интервала в виде

$\displaystyle ds^2=g_{00}\,dt^2+g_{11}dr^2+g_{22}(d\theta^2+\sin^2\theta\,d\varphi^2). $

Вид угловой части метрики $ (d\theta^2+\sin^2\theta\,d\varphi^2)$ следует из требования сферической симметрии. Из требования статичности находим, что $ g_{00}\,g_{11}$ и $ g_{22}$ должны быть функциями только $ r$. Кроме того, должно быть $ g_{01}=0$, иначе не будет обратимости во времени. Отсутствуют также члены типа $ g_{r\varphi}$ из-за сферической симметрии.

Определим радиальную координату $ r$ так, чтобы $ g_{22}=r^2$. При таком определении радиуса площадь сферы равна $ 4\pi r^2$, а длина окружности с центром в начале координат равна $ 2\pi r$. Однако это не значит, что точка, имеющая координату $ r$, удалена от центра на расстояние $ r$, так как геометрия теперь неевклидова.

Введем функции $ \nu(r)$ и $ \lambda(r)$ так, что

$\displaystyle g_{00}=-e^{\nu(r)},\,g_{11}=e^{\lambda(r)}, $

т. е. метрика приобретает вид

$\displaystyle ds^2=-e^{\nu(r)}dt^2+e^{\lambda(r)}dr^2+r^2(d\theta^2+\sin^2\theta\,d\varphi^2). $

Из уравнений Эйнштейна

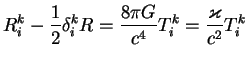
$\displaystyle R^k_i-{1\over 2}\delta^k_i R={8\pi G\over {c^4}}T^k_i={\varkappa\over{c^2}}T^k_i $

после довольно долгих вычислений получим

$\displaystyle e^{-\lambda}\left({\nu'\over r}+{1\over{r^2}}\right)-{1\over{r^2}}={\varkappa\over{c^2}}T^1_1,$ (9.1)

$\displaystyle -{1\over 2}e^{-\lambda}\left(\nu''+{{\nu'}^2\over 2}+{\nu'-\lambd... ...'\lambda'\over 2}\right)={\varkappa\over{c^2}}T^2_2={\varkappa\over{c^2}}T^3_3,$ (9.2)

$\displaystyle e^{-\lambda}\left({1\over{r^2}}-{\lambda'\over r}\right)-{1\over{r^2}}={\varkappa\over{c^2}}T^0_0.$ (9.3)

Все остальные уравнения обращаются в тождества 0=0. Не диагональные компоненты тензора энергии-импульса (типа $ T^{\varphi}_r$ и т. п.) обращаются в нуль вследствие сферической симметрии (это означает, что нет скалывающих напряжений). Отсутствует также компонента $ T_0^1$, так как этот член соответствует потоку энергии по радиусу, а мы рассматриваем статические решения.

Мы использовали смешанные компоненты тензора $ T^k_i$. В выражение $ T_{11}$ и $ T^{11}$ входят метрические коэффициенты. Пусть у нас есть метрика

$\displaystyle dl^2=a^2dx^2+b^2dy^2+c^2dz^2,$ (9.4)

которая эквивалентна метрике

$\displaystyle dl^2={dx'}^2+{dy'}^2+{dz'}^2,$ (9.5)

где $ a\,dx=x'$, $ b\,dy=dy'$, $ c\,dz=dz'$. Оказывается, что выражения для $ T_{11}$, например, разные в (9.4) и (9.5). В смешанные компоненты вида $ T^1_1$ коэффициенты $ a,\,b,\,c$ не входят, поэтому они одинаковы в исходной системе и локально-лоренцевой (если исходная система уже диагональна).

Начнем с того, что будем искать решение уравнений (9.1), (9.2), (9.3) в пустоте вокруг звезды (т. е. положим $ T^k_i=0$). Введем $ f=e^{-\lambda}$. Тогда

$\displaystyle -\lambda'\,e^{-\lambda}=f' $

$\displaystyle \lambda'=-f'/f. $

Теперь для уравнения (9.3) имеем

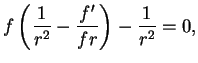
$\displaystyle f\left(\frac{1}{r^2}-{f'\over{fr}}\right)-{1\over{r^2}}=0, $

$ f=1-a/r,\,a$ -- const, т. е. $ g_{11}=e^{\lambda}=f^{-1}=1/(1-a/r)$. Вычитая из уравнения (9.1) уравнение (9.3), получим

$\displaystyle \nu'+\lambda'=0\,\Rightarrow\,\nu+\lambda=$const$\displaystyle . $

Выбор const просто определяет масштаб времени. Поэтому зададимся условием, что вдали от тела, где $ \lambda=0$, также и $ \nu=0$, т. е. переменная $ t$ есть время изменения далеким покоящимся наблюдателем. Тогда получим

$\displaystyle \nu+\lambda=0 $

Отсюда

$\displaystyle e^{\nu}=g_{00}=1-a/r. $

Мы получили известное решение Шварцшильда для пустого пространства вокруг сферического симметричного тела:

$\displaystyle ds^2=-c^2\left(1-{a\over r}\right)dt^2+{dr^2\over{1-{a\over r}}}+r^2(d\theta^2+\sin^2\theta\,d\varphi^2).$ (9.6)

При $ r\longrightarrow\infty$ эта метрика переходит в метрику Минковского.

Из выражения (6) видно, что при $ r=a$ коэффициент при $ dt^2$ обращается в нуль, а при $ dr^2$ -- в бесконечность.

Наблюдатель на некотором радиусе $ r$ пользуется локально-лоренцевой системой отсчета:

$\displaystyle ds^2=-c^2d\tau^2+dl^2. $

Для покоящегося наблюдателя в обеих системах $ dr,\,d\varphi,d\theta=0$ и $ dl=0$. Поскольку $ ds^2$ -- инвариант, получим

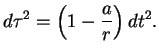
$\displaystyle d\tau^2=\left(1-\frac{a}{r}\right)dt^2. $

Вдали, при $ r\longrightarrow\infty$

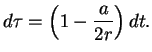
$\displaystyle d\tau=\left(1-{a\over{2r}}\right)dt. $

Так как мы уже выяснили связь потенциала с замедлением времени (раздел 8.4), мы видим, что

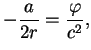
$\displaystyle -{a\over{2r}}={\varphi\over{c^2}}, $

где $ \varphi$ -- ньютоновский потенциал (мы убедимся в этом еще раз ниже, рассматривая движение частиц), но

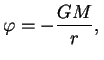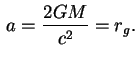
$\displaystyle \varphi=-{GM\over r},\,$т. е.$\displaystyle \,a={2GM\over{c^2}}=r_g. $

Величину $ r_g=a$ называют гравитационным радиусом (или радиусом Шварцшильда). Для звезды солнечной массы $ M=M_\odot=2\cdot10^{33}$ г; $ r_g=3\cdot10^5$ см=3 км (полезно запомнить!). Для Солнца метрику Шварцшильда можно применять до поверхности $ r_s=7\cdot10^{10}$ см, т. е. $ r_g/r$ всюду мало. Для нейтронных звезд $ r_g/r$ достигает $ 0,1\div 0,2$. Для черной (невращающейся!) дыры метрика Шварцшильда применима ко всей наблюдаемой области пространства, т. е. вплоть до $ r=r_g$. Почему область $ r<r_g$ не наблюдаема (издали) будет объяснено позднее.


<< 8.4 Гравитационное красное смещение. | Оглавление | 9.2 Движение частиц в ... >>

Публикации с ключевыми словами: Эволюция звезд - внутреннее строение звезд - термоядерные реакции - физические процессы
Публикации со словами: Эволюция звезд - внутреннее строение звезд - термоядерные реакции - физические процессы
См. также:
Все публикации на ту же тему >>

Обсудить эту публикацию
Оценка: 3.0 [голосов: 120]
 
О рейтинге
Версия для печати Распечатать

Астрометрия - Астрономические инструменты - Астрономическое образование - Астрофизика - История астрономии - Космонавтика, исследование космоса - Любительская астрономия - Планеты и Солнечная система - Солнце

Астронет | Научная сеть | ГАИШ МГУ | Поиск по МГУ | О проекте | Авторам

Комментарии, вопросы? Пишите: info@astronet.ru или сюда

Rambler's Top100 Яндекс цитирования