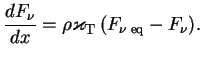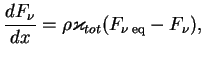<< 3.5 Рассеяние излучения на ... | Оглавление | 4.2 Коэффициент теплопро... >>
4. Теория переноса (продолжение)
Разделы
- 4.1 Перенос излучения при рассеянии
- 4.2 Коэффициент теплопроводности. Росселандово среднее
- 4.3 Поведение плотности и температуры вблизи поверхности горячей звезды
- 4.4 Критическая эддингтоновская светимость
- 4.5 Устойчивость теплового потока
- 4.6 Конвекция
4.1 Перенос излучения при рассеянии
В предыдущей главе было получено уравнение для изменения интенсивности при томсоновском рассеянии
![$\displaystyle {dF_\nu\over dx}=-\varkappa_{\mbox{\sc t}}\,\rho\,F_\nu,\;\varkappa_{\mbox{\sc t}}=0,4/\mu_e\;\left[{\mbox{см}^2
\over\mbox{г}}\right].
$](http://images.astronet.ru/pubd/2008/02/15/0001226214/img795.gif)
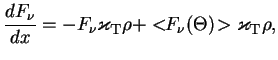
Нас интересует поток энергии излучения. Поскольку полного термодинамического
равновесия нет, в каждой точке должна быть зависимость ![]() от направления
(анизотропия). Однако эта анизотропия внутри звезды мала, и при усреднении по
всем направлениям мы получим величину, мало отличную от равновесной,
от направления
(анизотропия). Однако эта анизотропия внутри звезды мала, и при усреднении по
всем направлениям мы получим величину, мало отличную от равновесной,
Поэтому при рассеянии уравнение переноса имеет тот же вид, что и при поглощении:
Разница заключается в области применимости. Для тормозных процессов достаточно только равновесия плазмы, а излучение может быть существенно неравновесным и уравнение
где
В других условиях могут играть роль и другие механизмы непрозрачности, но эти остаются важными.
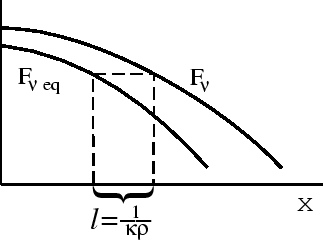
Как решать уравнение переноса (4.2)? В условиях ЛТР предлагается следующий метод последовательных приближений.
1-е приближение:
![]() (в оптически тонкой плазме
(в оптически тонкой плазме
![]() ).
).
2-е приближение: найдем малые отклонения от полного термодинамического равновесия.
Подставляя
![]() в левую часть (4.2), имеем вдоль луча с координатой
в левую часть (4.2), имеем вдоль луча с координатой
![]()
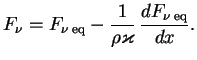
Величина
![]() , очевидно, есть длина свободного пробега кванта
, очевидно, есть длина свободного пробега кванта ![]() .
Предполагая, что
.
Предполагая, что
![]() , имеем
, имеем
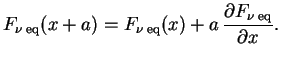
<< 3.5 Рассеяние излучения на ... | Оглавление | 4.2 Коэффициент теплопро... >>
|
Публикации с ключевыми словами:
Эволюция звезд - внутреннее строение звезд - термоядерные реакции - физические процессы
Публикации со словами: Эволюция звезд - внутреннее строение звезд - термоядерные реакции - физические процессы | |
См. также:
Все публикации на ту же тему >> | |