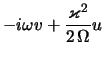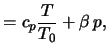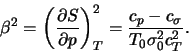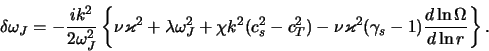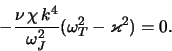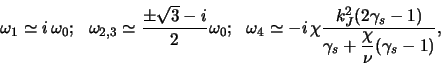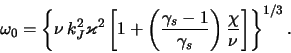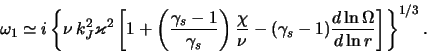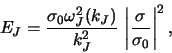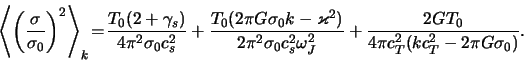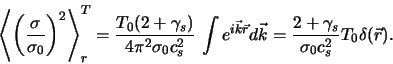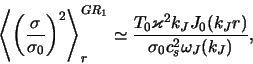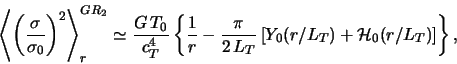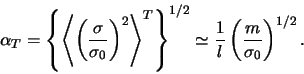---

<< 4.3 Неустойчивости газового грав... | Оглавление | 4.5 Гидродинамические неустойчивости ... >>

Разделы

• 4.4.1 Влияние диссипации на гравитационные и энтропийные возмущения
• 4.4.2 Быстрая диссипативная неустойчивость
• 4.4.3 Равновесные флуктуации в газовом диске

---

4.4 Диссипативные эффекты

При решении вопроса о гравитационной устойчивости газового диска и определении спектра колебаний в его плоскости учет диссипативных членов в первом приближении несуществен. Это можно проиллюстрировать следующей оценкой. Величина характерной "вязкой" частоты с по параметрам газового диска Галактики в окрестности Солнца (здесь -- молекулярная кинематическая вязкость). В то же время эпициклическая частота с .

Тем не менее исследование эффектов, связанных с учетом диссипативных членов, может привести к важным результатам. Во-первых, потому, что некоторые типы возмущений в плоскости газового диска могут обладать отрицательной энергией [2] и, следовательно, быть диссипативно неустойчивыми даже в гравитационно устойчивом диске. Во-вторых, учет диссипативных членов позволяет в принципе определить уровень равновесных флуктуаций, пользуясь флуктуационно-диссипативной теоремой [221,339]. Hаконец, мелкомасштабную туpбулентность можно учитывать в pамках диссипативной модели с эффективной (туpбулентной) вязкостью (см. п. 5.1.1).

4.4.1 Влияние диссипации на гравитационные и энтропийные возмущения

Используем приближение тонкого диска и ограничимся изучением коротковолновых осесимметричных возмущений. Для таких возмущений фурье-гармоники линеаризованных уравнений газодинамики с учетом диссипативных членов имеют вид [329] [сp. с (4.2.14)-(4.2.17)]

где ; , -- первая и вторая кинематические вязкости, -- возмущение энтpопии, -- коэффициент температуропроводности, -- удельная теплоемкость при постоянной плотности.

Система (4.4.1)-(4.4.4) должна быть дополнена уравнением Пуассона, коротковолновое решение которого имеет вид , и двумя термодинамическими соотношениями

где -- удельная теплоемкость при постоянном давлении и

Решая приведенную выше систему алгебраических уравнений, получим дисперсионное уравнение, описывающее свойства рассматриваемых возмущений

где ; . В бездиссипативном приближении из (4.4.8) получаем дисперсионное уравнение осесимметричных гравитационных возмущений

Выясним теперь влияние диссипации на эти возмущения. В соответствии с приведенными выше оценками полагаем , где . Тогда в линейном по диссипативным коэффициентам приближении получаем ( ; )

Поскольку , и в дисках плоских галактик , то в гравитационно устойчивом диске ( ) джинсовские возмущения затухают, а в гравитационно неустойчивом диске ( ) испытывают дополнительную дестабилизацию из-за диссипативных эффектов. Этот результат кажется естественным, так как джинсовские возмущения представляют собой звуковые () возмущения с учетом гироскопических эффектов () и самосогласованных возмущений гравитационного потенциала ( ). Звуковые же возмущения затухают [327]

и этот результат нетрудно получить из (4.4.9) в пределе коротковолновых () возмущений.

Общее дисперсионное уравнение (4.4.8) -- уравнение четвертой степени по . В бездиссипативном приближении из него следует, что кроме джинсовских , существует еще два (энтропийных) типа возмущений с . С учетом диссипации, полагая , для этих возмущений из (4.4.8) получаем упрощенное (квадратное по ) дисперсионное уравнение

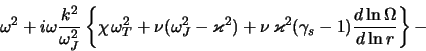
Если пренебречь теплопроводностью ( ) и считать диск твердотельно вращающимся, то из (4.4.11) следуют результаты работ [340,341]

и, следовательно, в гравитационно устойчивом ( ) газовом диске может развиваться диссипативная неустойчивость в области длин волн ^4.3. Учет конечной теплопроводности расширяет интервал диссипативно неустойчивых длин волн [329] до

Этот результат качественно согласуется с полученным Кумаром [342] для модели гравитирующего цилиндра.

4.4.2 Быстрая диссипативная неустойчивость

Из дисперсионного уравнения (4.4.11) следует, что инкремент диссипативной неустойчивости по порядку величины равен . Нетрудно также видеть, что учет дифференциальности вращения диска не меняет порядок величины этого результата. Эти результаты, однако, можно считать корректными только в том случае, если характерное время нестационарности диска много больше обратного инкремента. Характерное время динамической нестационарности , а характерное время тепловой нестационарности (эта оценка вытекает из уравнения баланса тепла). В общем случае инкремент диссипативных возмущений порядка и . Отсюда нетрудно видеть, что . Таким образом, характерные времена тепловой нестационарности диска и развития диссипативной неустойчивости оказываются одного порядка.

В связи со сказанным выше обратим внимание на следующее обстоятельство [343]. Инкремент диссипативной неустойчивости (равно как и декремент затухания гравитационных возмущений) по порядку величины равен за пределами довольно узкой зоны волновых чисел, лежащей в окрестности . Но для близкого к границе гравитационной устойчивости диска в пределах указанной зоны волновых чисел инкремент диссипативной неустойчивости оказывается порядка . Ясно, что в таком диске возможно , или иначе

и, следовательно, приведенные выше результаты в малой окрестности будут неприменимы. В этом случае термин "гравитационные возмущения" теряет смысл и дисперсионные свойства всех четырех типов возмущений должны определяться из общего дисперсионного уравнения (4.4.8), решения которого при и имеют вид (без учета дифференциальности вращения диска)

где

Из этого спектра решений неустойчивыми являются только возмущения с и их инкремент

а остальные решения соответствуют затухающим возмущениям.

Учитывая тот факт, что по порядку величины и ( -- длина свободного пробега частиц), нетрудно видеть, что . Поэтому диссипативная неустойчивость (4.4.14) является быстрой и для динамических процессов, определяемых этой неустойчивостью, тепловая нестационарность диска несущественна.

Нетрудно обобщить результат (4.4.14) и на случай дифференциально вращающегося диска. В пределе из исходного дисперсионного уравнения (4.4.8) получаем

Поскольку и для астрофизических дисков , то нетрудно видеть, что по порядку величины инкремент (4.4.16) оказывается таким же, как в случае твердотельного вращения. Таким образом, учет дифференциальности вращения диска не вносит ничего принципиально нового в динамику диссипативной неустойчивости.

В наиболее коротковолновом пределе [см. (4.4.12)] диссипативная неустойчивость не имеет места. Это естественным образом наводит на мысль, что диссипативная раскачка возмущений в гравитационно устойчивом диске обусловлена влиянием возмущений гравитационного поля, существенным в области длин волн . Как показали Фридман и Поляченко [2], это влияние проявляется в том, что плотность энергии диссипативно неустойчивых возмущений является отрицательной ( ). В этом случае диссипация энергии возмущений ( ) эквивалентна росту ее абсолютной величины и, следовательно, росту амплитуды возмущения. Действительно, для диссипативно неустойчивых возмущений (4.4.14) с частотой [343]

где -- возмущенная поверхностная плотность диска.

Аналогичные вычисления плотности энергии гравитационных возмущений при приводят к следующему результату:

откуда видно, что . Поэтому джинсовские возмущения с учетом диссипативных факторов в гравитационно устойчивом диске затухают и дополнительно неустойчивы в гравитационно неустойчивом диске [см. (4.4.9)].

4.4.3 Равновесные флуктуации в газовом диске

Для вычисления уровня равновесных шумов в гравитирующем газовом диске используем флуктуационно-диссипативную теорему [221] и гидродинамическую теорию флуктуаций [339]. Для простоты ограничимся моделью однородного твердотельно вращающегося ( ) диска и, рассматривая коротковолновые возмущения, ориентируем ось "" вдоль направления волнового вектора . Фурье-гармоники газодинамических уравнений с учетом сторонних сил, вводимых для вычисления тензора обобщенной восприимчивости во вращающейся вместе с диском системе отсчета, имеют вид [344]

где , , . Эта система должна быть дополнена термодинамическими соотношениями (4.4.5), (4.4.6) и уравнением Пуассона ( ). Учет диссипативных членов в (4.4.19)-(4.4.22) необходим для обхода полюсов в комплексной -плоскости при обратном фурье-преобразовании спектральной плотности шумов. В окончательный ответ -- величину уровня шумов -- диссипативные коэффициенты не войдут, поскольку . Поэтому для упрощения вычислений положим .

Диссипация энергии в газовом диске под действием сторонних сил определяется выражением

где интегрирование проводится по поверхности диска, а , -- обобщенные координаты и сторонние силы, спектральная связь между которыми определяется соотношением [221]

где -- тензор обобщенной восприимчивости.

В качестве обобщенных координат выберем величины , , . Тогда (). Используя эти определения и решая приведенную выше систему, можно получить компоненты тензора обобщенной восприимчивости. Используя основную формулу флуктуационно-диссипативной теоремы [221], записанную для плоского случая

спектральный уровень флуктуаций поверхностной плотности можно представить в виде [344]

Здесь не зависящий от волнового числа первый член -- спектральная плотность термодинамических шумов, а второй и третий члены можно назвать спектральной плотностью "гравитационно-вращательных" шумов. Вычисляя корреляционную функцию термодинамических шумов, получаем

Отсутствие пространственной корреляции термодинамических шумов следует рассматривать как указание на то, что характерный размер корреляции в этом случае оказывается порядка минимально возможного в гидродинамике размера -- длины свободного пробега частиц . Таким образом, в (4.4.27) следует полагать .

Спектральная плотность "гравитационно-вращательных" шумов, представленная вторым в (4.4.26) членом, в диске, близком к границе гравитационной устойчивости [ ], имеет резкий максимум в окрестности , где . С учетом этого обстоятельства получаем

где -- функция Бесселя первого рода. Наконец, интегрирование последнего в (4.4.26) члена дает

где , , -- функции Неймана и Струве соответственно.

Получим соотношения для оценок уровня шумов. Поскольку , где -- характерная масса "частиц" диска, то для термодинамических шумов (4.4.27) с учетом того, что , получаем

Для нетермодинамических флуктуаций (4.4.28) характерный пространственный масштаб , а их интенсивность в масштабах с учетом результата (4.4.14) может быть оценена как

Наконец, характерный масштаб нетермодинамических шумов (4.4.29) порядка , а их максимальная интенсивность (при )

В качестве примера применения изложенной выше теории оценим уровень равновесных шумов в солнечной окрестности газовой подсистемы Галактики. Будем считать, что дисперсия скоростей газовых облаков -- "макроатомов" диска км/с, их характерные радиус и масса равны пк и М соответственно. Используя также данные о параметрах газового диска в окрестности Солнца: с; М/пк; пк, получаем пк, число облаков в единице объема пк. Поскольку газовые облака -- отнюдь не твердые сферы, считаем, что эффективный (столкновительный) радиус среднего облака несколько меньше наблюдаемого (пусть ). Тогда сечение взаимодействия облаков пк, а длина свободного пробега пк. В результате получаем

Высокий уровень шумов, предсказываемый этими оценками, означает, что флуктуационные структуры в газовой подсистеме Галактики могут быть в принципе наблюдаемыми. Характерные размеры наиболее интенсивных из этих структур (термодинамических) оказываются порядка длины свободного пробега облаков (нескольких межоблачных расстояний), и такие комплексы могут содержать до нескольких десятков облаков. Несколько менее интенсивные нетермодинамические флуктуации имеют характерные размеры (по параметрам газовой подсистемы в окрестности Солнца это кпк и могут, по-видимому, обеспечить затравочные возмущения для тех или иных особенностей спирального узора (ответвления от спиралей и т.п.).

---

<< 4.3 Неустойчивости газового грав... | Оглавление | 4.5 Гидродинамические неустойчивости ... >>

Публикации с ключевыми словами: аккреционный диск - диск, галактический - гидродинамика - спиральная структура Публикации со словами: аккреционный диск - диск, галактический - гидродинамика - спиральная структура
См. также: Искривленный диск NGC 4753 Аккреционный диск черной дыры: визуализация Дважды искривленный мир двойных черных дыр Спиральный диск вокруг черной дыры В центре спиральной галактики NGC 3521 Массивная черная дыра разрывает пролетающую звезду Ультрафиолетовые кольца M31 Все публикации на ту же тему >>