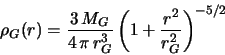<< 3.3 Гравитационная устойчивость ... | Оглавление | 3.5 Построение устойчивых ... >>
- 3.4.1 Рассеяние на ГМО
- 3.4.2 Коллективные процессы
- 3.4.3 Влияние газа на развитие бар-моды
- 3.4.4 Почему встречаются тонкие звездные диски?
3.4 Релаксационные процессы в звездном диске
Обсуждению причин, которые могли бы объяснить наблюдаемую корреляцию между возрастом, дисперсией скоростей звезд и их шкалой высот, посвящено множество работ (см., например, монографию Марочника и Сучкова [7] и ссылки там; разд. 1.1). В данном разделе обсудим результаты только некоторых численных экспериментов, которые могли бы приблизить нас к пониманию природы связи между кинематическими параметрами и их эволюцией.
Наблюдения свидетельствуют об эволюции функции распределения скоростей звезд. В то же время звездно-звездные сближения в этом смысле заведомо неэффективны. Изменение скорости звезды в результате рассеяния пропорционально величине рассеивающей массы. Поэтому гигантские молекулярные облака (ГМО) могут служить важным фактором, влияющим на динамику звездного диска. Большие массы и размеры ГМО (см. разд. 1.2) позволяют эффективно рассеиваться на них звездам, что приводит к релаксационным процессам, увеличивая эффективную температуру звездного населения. Рассеяние на массивных неточечных объектах (например, ГМО) как возможный механизм изменения распределения скоростей звезд неоднократно обсуждался [295-299]. Его можно условно назвать механическим в отличие от описанного в разд. 2.5, где уже рассматривалась проблема анизотропии в распределении скоростей звезд и с точки зрения коллективных процессов -- устойчивости относительно изгибных мод. Ниже обсудим эти два механизма подробнее.
3.4.1 Рассеяние на ГМО
Приведем некоторые результаты численного моделирования
динамики звездного диска с учетом ГМО, следуя работам Вилумсена [244,245].
Рассматривалась следующая модель. Распределение плотности
звездного населения диска выбиралось в виде [ср. с (2.1.45)]
Распределению плотности вещества в ГМО
соответствует потенциал
Взаимодействие между звездами и ГМО учитывалось, только если расстояние между ними не превышало
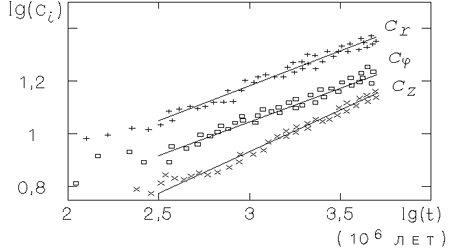 |
Рис. 3.7. Аппроксимация
временной зависимости
компонент (
|
На рис. 3.7 показана динамика трех компонент дисперсии
скоростей звезд. В конце моделирования получается следующее
отношение этих компонент для произвольной радиальной координаты:
где
Для полной экспериментальной дисперсии скоростей (см. рис. 3.7) и теоретической зависимости (3.4.7) в случае
В табл.3.1 приведены значения теоретической величины
| 4.2 | 5.1 | 6.0 | 7.0 | 8.1 | 9.3 | |
| -2.27 | -2.38 | -2.47 | -2.53 | -2.64 | -2.63 | |
| -2.12 | -2.19 | -2.24 | -2.35 | -2.42 | -2.51 | |
|
|
1.41 | 1.55 | 1.70 | 1.51 | 1.66 | 1.32 |
В связи с наблюдаемой зависимостью толщины звездного диска от
возраста звезд упомянем также о возрастании со временем в
экспериментах Вилумсена величины ![]() :
:
В моделях Ясумоту и Фудзимото [299] варьировались в широких пределах параметры, описывающие подсистему ГМО, помимо которых в рассмотрение включались спиральные волны плотности. В начале экспериментов звездные диски задавались холодными и на первом этапе наблюдался резкий рост дисперсии скоростей, затем, начиная с
Временная зависимость дисперсии в солнечной окрестности
Галактики, по данным Вилена [54], имеет вид ![]() ,
,
![]() (вывод сделан исходя из данных наблюдений для различных
спектральных классов звезд). Как видим, достигнутые в
экспериментах значения
(вывод сделан исходя из данных наблюдений для различных
спектральных классов звезд). Как видим, достигнутые в
экспериментах значения
![]() меньше наблюдаемых для
меньше наблюдаемых для
![]() - и
- и ![]() -типов звезд величин
-типов звезд величин ![]() км/с.
км/с.
Следует сказать о том, что еще в 1961 г. Кузминым [296] были
получены весьма близкие результаты. В рамках предположения, что
гравитационное взаимодействие звезд с облаками диффузной материи
должно приводить к росту как радиальной, так и вертикальной
компонент дисперсии скоростей звезд, в равновесном пределе (
![]() const) была получена следующая величина анизотропии:
const) была получена следующая величина анизотропии:
Итак, если эволюция функции распределения скоростей звезд
определяется процессом рассеяния звезд на массивных облаках газа,
то для подсистемы наиболее старых звезд диска
![]() . Следует, однако, помнить, что рассмотренные выше модели достаточно
грубо учитывают реальное распределение в пространстве рассеивающих
объектов и их динамику на временах, сравнимых со временем жизни
Галактики. В то же время надежные наблюдаемые значения величины
. Следует, однако, помнить, что рассмотренные выше модели достаточно
грубо учитывают реальное распределение в пространстве рассеивающих
объектов и их динамику на временах, сравнимых со временем жизни
Галактики. В то же время надежные наблюдаемые значения величины
![]() относятся только к достаточно малой окрестности Солнца.
относятся только к достаточно малой окрестности Солнца.
3.4.2 Коллективные процессы
В данном пункте обсудим проблему анизотропии дисперсии
скоростей звезд без привлечения массивных рассеивающих объектов.
Мы уже видели, что согласно условию устойчивости относительно
мелкомасштабных изгибных возмущений
![]() (п. 2.5.2). Заметим, что этот результат получен в рамках
модели однородного невращающегося звездного слоя без учета влияния
сферической подсистемы, а учет этих факторов требует численного
моделирования. Для изучения проблемы анизотропии дисперсии
скоростей была поставлена серия экспериментов [300], в которых
менялись начальное отношение
(п. 2.5.2). Заметим, что этот результат получен в рамках
модели однородного невращающегося звездного слоя без учета влияния
сферической подсистемы, а учет этих факторов требует численного
моделирования. Для изучения проблемы анизотропии дисперсии
скоростей была поставлена серия экспериментов [300], в которых
менялись начальное отношение ![]() и параметры гало
и параметры гало ![]() и
и ![]() в
(3.1.5) с
в
(3.1.5) с ![]() . Рассматривалось "рыхлое" ядро сферической подсистемы (
. Рассматривалось "рыхлое" ядро сферической подсистемы (![]() ) и "точечное" ядро (
) и "точечное" ядро (![]() ). В качестве начальных условий
принималось отношение
). В качестве начальных условий
принималось отношение
![]() , что соответствует наблюдаемому
в Галактике по всем звездам.
, что соответствует наблюдаемому
в Галактике по всем звездам.
В системах с "рыхлым" ядром гало в течение первого
полуоборота происходят быстрое убывание ![]() и медленный рост
и медленный рост
![]() , что приводит исследуемые модели на границу устойчивости
диска относительно изгибных возмущений. Уже после первого оборота
диска во всех моделях с
, что приводит исследуемые модели на границу устойчивости
диска относительно изгибных возмущений. Уже после первого оборота
диска во всех моделях с ![]() величина
величина
![]() . При этом
. При этом ![]() оказывается в среднем ближе к верхней
из указанных границ в моделях с не очень массивным гало (
оказывается в среднем ближе к верхней
из указанных границ в моделях с не очень массивным гало (
![]() ) и ближе к нижней в системе с
) и ближе к нижней в системе с ![]() . Еще ярче это различие
между моделями с различными массами сферических подсистем проявилось в
случае концентрированного ядра (
. Еще ярче это различие
между моделями с различными массами сферических подсистем проявилось в
случае концентрированного ядра (![]() ). Так, в моделях с
). Так, в моделях с
![]() в среднем выполнялось
в среднем выполнялось
![]() , причем чем ближе к центру диска и чем
гало маломассивнее, тем с большим запасом выполняется критерий
устойчивости. Отклонение в большую сторону величины
, причем чем ближе к центру диска и чем
гало маломассивнее, тем с большим запасом выполняется критерий
устойчивости. Отклонение в большую сторону величины ![]() от
критического значения
от
критического значения ![]() может быть связано с неоднородностью диска
по
может быть связано с неоднородностью диска
по ![]() -координате. Действительно, критерий (2.5.18) получен в модели
однородного звездного слоя с резкими границами. Поэтому при приближении
к
-координате. Действительно, критерий (2.5.18) получен в модели
однородного звездного слоя с резкими границами. Поэтому при приближении
к ![]() вертикальная компонента скорости стремится к нулю и
тем самым величина
вертикальная компонента скорости стремится к нулю и
тем самым величина ![]() -дисперсии оказывается меньше, чем в моделях
неоднородного диска, в которых
-дисперсии оказывается меньше, чем в моделях
неоднородного диска, в которых
![]() .
В противоположность этому учет массы гало может привести к уменьшению
маргинального значения
.
В противоположность этому учет массы гало может привести к уменьшению
маргинального значения ![]() .
.
Сходные результаты были получены в [290], численный
эксперимент которых включал достаточно массивное (![]() ) и
"рыхлое" (
) и
"рыхлое" (
![]() ) гало. В большей части диска (
) гало. В большей части диска (
![]() ) на протяжении всего
эксперимента
отношение
) на протяжении всего
эксперимента
отношение
![]() оставалось практически постоянным. В то же
время на далекой периферии наблюдалось некоторое уменьшение данного
параметра, вплоть до
оставалось практически постоянным. В то же
время на далекой периферии наблюдалось некоторое уменьшение данного
параметра, вплоть до
![]() .
Последний эффект, по-видимому, обусловлен тем, что в этой области (
.
Последний эффект, по-видимому, обусловлен тем, что в этой области (
![]() ) поверхностная плотность
изменяется очень резко -- масштаб
) поверхностная плотность
изменяется очень резко -- масштаб ![]() уменьшается от
уменьшается от ![]() кпк до
кпк до ![]() кпк. Такая сильная неоднородность диска требует
для стабилизации гравитационной неустойчивости высоких значений
дисперсии радиальных скоростей
кпк. Такая сильная неоднородность диска требует
для стабилизации гравитационной неустойчивости высоких значений
дисперсии радиальных скоростей ![]() , так что величина
, так что величина ![]() в области
в области
![]() кпк практически перестает падать с ростом
кпк практически перестает падать с ростом ![]() .
.
3.4.3 Влияние газа на развитие бар-моды
В газовом самогравитирующем диске, как и в звездном, может
развиваться бар-мода3.8. Однако из-за столкновительности газа
неустойчивость (а она имеет гравитационную природу) проще
стабилизировать, в отличие от бесстолкновительного звездного диска
[см. (3.2.4)] достаточно выполнения
![]() [287]. Вандервоорт
[303] в рамках линейного анализа устойчивости твердотельно
вращающегося однородного звездно-газового сфероида показал, что
критическое значение
[287]. Вандервоорт
[303] в рамках линейного анализа устойчивости твердотельно
вращающегося однородного звездно-газового сфероида показал, что
критическое значение ![]() лежит в пределах
лежит в пределах
![]() в
зависимости от параметров модели и прежде всего от доли массы газа в системе
в
зависимости от параметров модели и прежде всего от доли массы газа в системе
![]() .
.
Как мы знаем, галактический газ является сильно неоднородной
на малых масштабах средой. Наблюдается целая иерархия газовых
облаков, различающихся своими размерами и массами. В предыдущих
пунктах мы уже видели, что на массивных газовых облаках (ГМО и
более крупномасштабных образованиях -- ассоциациях) происходит
эффективное рассеяние, переводящее орбитальное движение звезд и
газа в тепловое. Таким образом, облачная структура газа является
важным фактором стабилизации глобальных мод. Характерные времена
образования и жизни облаков сравнимы со временем образования бара
(
![]() лет). Поэтому для выяснения роли газа в подавлении
бар-моды необходимо детальное рассмотрение процессов образования
облаков, их динамику и звездообразования. Вклад в нагрев диска
дает и динамическое трение: при движении тяжелых газовых облаков
легкие звезды испытывают гравитационную фокусировку, образуя
повышенную концентрацию за облаком.
лет). Поэтому для выяснения роли газа в подавлении
бар-моды необходимо детальное рассмотрение процессов образования
облаков, их динамику и звездообразования. Вклад в нагрев диска
дает и динамическое трение: при движении тяжелых газовых облаков
легкие звезды испытывают гравитационную фокусировку, образуя
повышенную концентрацию за облаком.
Недавние численные эксперименты, учитывающие
вышеперечисленные эффекты, наглядно продемонстрировали чрезвычайно
важную роль газа в динамике звездного диска [304,305]. Оказалось,
что газ может стабилизировать бар-моду, если он составляет всего
несколько процентов от общей массы. Разумеется, критическое
значение величины
![]() зависит от многочисленных параметров
модели, однако, по-мнению авторов вышеперечисленных работ, для
типичных галактик можно принять
зависит от многочисленных параметров
модели, однако, по-мнению авторов вышеперечисленных работ, для
типичных галактик можно принять
![]() (здесь
следует учитывать газ и звезды, находящиеся в области формирования бара).
(здесь
следует учитывать газ и звезды, находящиеся в области формирования бара).
Обсудим подробнее этот результат. Для распределения
поверхностной плотности в диске
![]() критерий
устойчивости по порядку величины можно записать в виде [306]
критерий
устойчивости по порядку величины можно записать в виде [306]
здесь
Как видим, нагрев звездной подсистемы весьма сильно зависит от плотности газового диска и, как показывают численные эксперименты, в случае
3.4.4 Почему встречаются тонкие звездные диски?
Как отмечалось в п. 1.1.2, типичные значения полутолщины
звездного диска составляют
![]() кпк. Причем достаточно
многочисленны наблюдаемые с ребра галактики с отношением видимых
полуосей
кпк. Причем достаточно
многочисленны наблюдаемые с ребра галактики с отношением видимых
полуосей
![]() . Относительную толщину звездного диска
естественно определить отношением
. Относительную толщину звездного диска
естественно определить отношением
![]() . В случае
распределения объемной плотности
. В случае
распределения объемной плотности
![]() (см. разд. 1.1) можно принять
(см. разд. 1.1) можно принять
![]() [104].
Тем самым для тонких звездных дисков (
[104].
Тем самым для тонких звездных дисков (
![]() ) считаем
) считаем
![]() . Следуя работе [104], определим условия, при которых стационарные
звездные диски могут иметь такую толщину.
. Следуя работе [104], определим условия, при которых стационарные
звездные диски могут иметь такую толщину.
Стационарная система должна быть, во-первых, гравитационно
устойчива относительно возмущений, лежащих в плоскости диска, что
накладывает ограничения на дисперсию радиальных скоростей
В свою очередь полутолщина диска
Круговая скорость
Для экспоненциального профиля плотности (1.1.2) масса диска
Для плоской кривой вращения
где
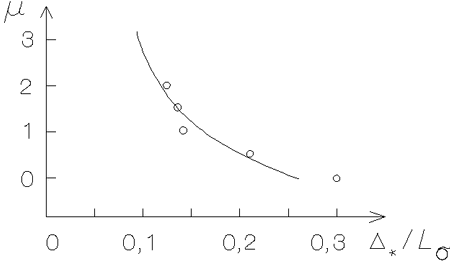 |
Рис. 3.8. Связь между
относительной толщиной
стационарного звездного
диска |
Из (3.4.15) видно, что с увеличением массы гало полутолщина
звездного диска уменьшается. Для уточнения данного соотношения
обратимся к результатам численных экспериментов, представленным на
рис. 3.8 [104]. Отличие зависимости (3.4.15) от экспериментальной
для ![]() , по-видимому, связано с плохим выполнением эпициклического
приближения (
, по-видимому, связано с плохим выполнением эпициклического
приближения (
![]() ), которое лежит в основе критерия
устойчивости, а следовательно, соотношения (3.4.15).
), которое лежит в основе критерия
устойчивости, а следовательно, соотношения (3.4.15).
Как видим, диск без гало (![]() ) имеет
) имеет
![]() . Для
существования тонких галактик (
. Для
существования тонких галактик (
![]() ) необходимо присутствие
сферической компоненты с
) необходимо присутствие
сферической компоненты с ![]() . Для наиболее тонких
("иглообразных") галактик с
. Для наиболее тонких
("иглообразных") галактик с
![]() имеем
имеем ![]() .
.
<< 3.3 Гравитационная устойчивость ... | Оглавление | 3.5 Построение устойчивых ... >>
|
Публикации с ключевыми словами:
аккреционный диск - диск, галактический - гидродинамика - спиральная структура
Публикации со словами: аккреционный диск - диск, галактический - гидродинамика - спиральная структура | |
См. также:
Все публикации на ту же тему >> | |