Астронет > Колебания и волны

по текстам по ключевым словам в глоссарии по сайтам перевод

Колебания и волны. Лекции.

В.А.Алешкевич, Л.Г.Деденко, В.А.Караваев (Физический факультет МГУ)
Издательство Физического факультета МГУ, 2001 г. Содержание

Определим теперь скорость $c_{p}$ движения этой волны. Для этого проследим за движением гребня волны, вершина которого в некоторый момент времени находится в точке $М.$ Пусть за время $\Delta t$ этот гребень сместится на расстояние $\Delta x_{n} \gg a.$ Поскольку на вершине гребня массы имеют максимальное положительное смещение, то фаза их колебаний постоянна и равна

$\omega _{p} t - k_{p} x_{n} = {\displaystyle \frac{\displaystyle {\displaystyle \pi }}{\displaystyle {\displaystyle 2}}}.$

(4.11)

Поэтому

$\omega _{p} \Delta t - k_{p} \Delta x_{n} = 0.$

(4.12)

Отсюда скорость $c_{p}$ получается равной

$c_{p} = {\displaystyle \frac{\displaystyle {\displaystyle \Delta x_{n} }}{\displaystyle {\displaystyle \Delta t}}} = {\displaystyle \frac{\displaystyle {\displaystyle \omega _{p} }}{\displaystyle {\displaystyle k_{p} }}} = \nu _{p} \cdot \lambda _{p}.$

(4.13)

Скорость $c_{p}$ называется фазовой скоростью гармонической волны с частотой $\omega _{p} = 2\pi \nu _{p}.$ Проанализируем зависимость этой скорости от волнового числа, пользуясь дисперсионным соотношением (4.1). Для этого перепишем его с учетом (4.4) в виде:

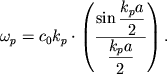$\omega _{p} = c_{0} k_{p} \cdot \left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle \sin {\displaystyle \frac{\displaystyle {\displaystyle k_{p} a}}{\displaystyle {\displaystyle 2}}}}}{\displaystyle {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle k_{p} a}}{\displaystyle {\displaystyle 2}}}}}}} \right).$

(4.14)

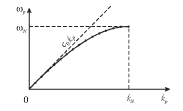
График зависимости (4.14) называется дисперсионной кривой и изображен на рис. 4.5а.

Рис. 4.5а.

На этой кривой точками отмечены значения частот $\omega _{p}$ и волновых чисел $k_{p}.$ Пунктиром изображена прямая $\omega _{p} = c_{0} k_{p}.$ Она получается из (4.14) предельным переходом при $a \to 0$ (непрерывная среда).

Из формулы (4.14) или из рис. 4.5а можно сделать ряд принципиально важных выводов.

1) Из нелинейной зависимости $\omega _{p} = \omega (k_{p} ),$ описываемой формулой (4.14), следует, что фазовая скорость гармонической волны $c_{p} = \omega _{p} / k_{p}$ зависит от $k_{p}$ (или от $\omega _{p}$ ):

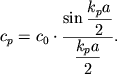$c_{p} = c_{0} \cdot {\displaystyle \frac{\displaystyle {\displaystyle \sin {\displaystyle \frac{\displaystyle {\displaystyle k_{p} a}}{\displaystyle {\displaystyle 2}}}}}{\displaystyle {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle k_{p} a}}{\displaystyle {\displaystyle 2}}}}}}.$

(4.15)

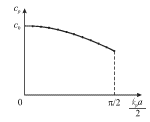
Зависимость (4.15) изображена на рис. 4.5б.

Рис. 4.5б.

Это явление носит название дисперсии среды по отношению к распространяющейся в ней волне. Эквивалентным является выражение "дисперсия волны в среде". Если фазовая скорость волны не зависит от $k_{p},$ как, например, в случае непрерывной среды, то говорят, что дисперсия отсутствует.

2) Для маленьких волновых чисел ( $k_{p} a \ll 1,$ или $\lambda _{p} \gg a$ ) дисперсия мала. Скорость таких "длинных волн" $c_{p} \approx c_{0},$ и среда может считаться сплошной.

3) С увеличением волнового числа $k_{p}$ (а значит и $\omega _{p}$ ) скорость $c_{p},$ как это следует из (4.15), убывает. Такое поведение скорости называется нормальной дисперсией. Следует отметить, что в оптике, помимо этой, реализуется и другая ситуация, когда фазовая скорость света в некотором диапазоне частот может возрастать с увеличением частоты. В этом случае дисперсия называется аномальной.

4) Дисперсионная кривая заканчивается, когда волновое число и частота достигают максимальных значений $k_{N}$ и $\omega _{N}.$ Они получаются из (4.14) и (4.1) при $N \gg 1$ :

$k_{N} = {\displaystyle \frac{\displaystyle {\displaystyle \pi }}{\displaystyle {\displaystyle a}}}; \quad \omega _{N} = 2\Omega.$

Это означает, что волны с частотой $\omega \gt \omega _{N}$ в такой среде распространяться не могут. Действительно, при частоте $\omega = \omega _{N}$ длина волны $\lambda _{N} = 2\pi / k_{N} = 2a.$ Волны с меньшей длиной волны не могут существовать, поскольку на длине распространяющейся волны должно находиться не меньше двух колеблющихся грузов.

Заметим, что в некоторых случаях, например, при распространении электромагнитных волн в твердом теле и в плазме, кривая дисперсии может начинаться с некоторой точки на оси частот $\omega (0).$ В таких средах могут распространяться электромагнитные волны только с частотами $\omega,$ лежащими внутри интервала $\omega (0) \lt \omega \le \omega _{N}.$

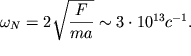В качестве примера укажем, что для кристаллов величина $F / a\sim 15 Н/м$ ( $F$ - упругая сила, величина которой определяется межатомным взаимодействием). Если принять массу иона равной $m\sim 6 \cdot 10^{ - 26} кг,$ то $\omega _{N} = 2\sqrt {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle F}}{\displaystyle {\displaystyle ma}}}} \sim 3 \cdot 10^{13} c^{ - 1}.$ Эта частота, как и частоты колебаний молекул CO₂ и H₂O, лежит в инфракрасной области электромагнитного спектра. Поэтому при распространении ИК излучения в кристаллах ионы могут совершать резонансные колебания. В этом частотном оптическом диапазоне может существовать сильная дисперсия света.

Отметим, что при распространении волн в протяженных средах проблемы "настройки" частоты $\omega$ внешнего воздействия, порождающего волну, на частоту $\omega _{p}$ одной из мод среды не существует. Любое воздействие внешней силы, даже сколь угодно близкой к гармонической, на самом деле всегда будет квазигармоническим, характеризуемым узким интервалом частот $\Delta \omega \ll \omega.$ С другой стороны, для протяженной среды к частоте $\omega$ будут близки частоты $\omega _{p}$ мод с большими номерами $р (p \gg 1).$ Разность частот двух соседних мод $\Delta \omega _{p} = \omega _{p + 1} - \omega _{p},$ как это легко видеть из рисунка 4.5, будет настолько малой, что $\Delta \omega _{p} \ll \Delta \omega.$ Следовательно, для любой частоты $\omega$ внешнего воздействия, прикладываемого к границе среды, по ней побежит волна, которую в ряде случаев можно приближенно считать гармонической:

$s(x,t) = s_{0} \sin (\omega t - kx).$

(4.16)

Группа волн и ее скорость.

Как и внешнее воздействие, волна, возникающая в среде, будет, строго говоря, квазигармонической, т. к. $\Delta \omega _{p} \ll \Delta \omega.$ Поэтому вместо (4.16) следует записать уравнение волны в более усложненном виде:

$s(x,t) = s_{0} (x,t)\sin [\omega _{0} t - k_{0} x + \varphi _{0} (x,t)].$

(4.17)

Здесь амплитуда $s_{0} (x,t)$ и фаза $\varphi _{0} (x,t)$ являются медленно меняющимися функциями времени на некотором масштабе времени $\tau$ (сравните с формулой (3.19)). Естественно, что такая волна представляет собой группу гармонических волн, частоты которых располагаются вблизи основной частоты $\omega _{0}$ в пределах интервала $\Delta \omega \approx 2\pi / \tau.$ Каждая из волн группы в среде с дисперсией имеет собственную фазовую скорость. В среде с нормальной дисперсией волны большей частоты будут двигаться медленнее, чем волны меньшей частоты. Возникает естественный вопрос: что является скоростью группы волн, и если такая скорость существует, то как ее вычислить? Какой физический смысл имеет эта скорость и в чем ее отличие от фазовой скорости ?

Чтобы ответить на эти вопросы, рассмотрим для простоты группу из двух волн с одинаковыми амплитудами $s_{0}$ и с близкими частотами $\omega _{1}$ и $\omega _{2},$ бегущих в положительном направлении оси х. Будем считать, что $\Delta \omega = \omega _{2} - \omega _{1} \ll \omega _{0} = {\displaystyle \frac{\displaystyle {\displaystyle \omega _{1} + \omega _{2} }}{\displaystyle {\displaystyle 2}}}.$ С такой ситуацией мы уже встречались при анализе биений двух связанных осцилляторов. Зададим дисперсионные свойства среды дисперсионным соотношением $\omega = \omega (k).$ С его помощью вычислим значения $k_{1}$ и $k_{2}$ двух волновых чисел, соответствующих частотам $\omega _{1}$ и $\omega _{2}.$ Тогда уравнение группы волн примет вид:

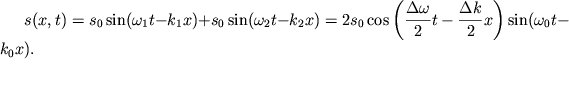$s(x,t) = s_{0} \sin (\omega _{1} t - k_{1} x) + s_{0} \sin (\omega _{2} t - k_{2} x) = 2s_{0} \cos \left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle \Delta \omega }}{\displaystyle {\displaystyle 2}}}t - {\displaystyle \frac{\displaystyle {\displaystyle \Delta k}}{\displaystyle {\displaystyle 2}}}x} \right)\sin (\omega _{0} t - k_{0} x).$

(4.18)

Здесь $\Delta k = k_{2} - k_{1}, k_{0} = {\displaystyle \frac{\displaystyle {\displaystyle k_{1} + k_{2} }}{\displaystyle {\displaystyle 2}}}.$

Назад| Вперед

Публикации с ключевыми словами: колебания - волны Публикации со словами: колебания - волны
См. также: Колебания и волны

Обсудить эту публикацию

Версия для печати

Астрометрия - Астрономические инструменты - Астрономическое образование - Астрофизика - История астрономии - Космонавтика, исследование космоса - Любительская астрономия - Планеты и Солнечная система - Солнце