Астронет > 1.2 Суперпотенциал Каца-Крушциела -- обобщенный суперпотенциал Фрейда

по текстам по ключевым словам в глоссарии по сайтам перевод по каталогу

<< 1.1 Классические псевдотензоры и ... | Оглавление | 1.3 Построение сохраняющихся токов ... >>

1.2 Суперпотенциал Каца-Крушциела -- обобщенный суперпотенциал Фрейда

Нарисованная выше картина о законах сохранения в ОТО требует своего обобщения и развития. Какие же моменты должны быть учтены? Мы бы определили их так:

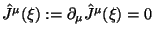(i) Законы сохранения и сохраняющиеся величины должны определяться сохраняющимся током (векторной плотностью): $\hat J^\mu(\xi) := \partial_\mu \hat J^\mu (\xi) = 0$ .
(ii) Построение 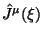$\hat J^\mu(\xi)$ определяется лавгранжианом и процедурой Нетер.
(iii) Модель должна быть ковариантной на выбранном фоне.
(iv) Законы сохранения должны ,,работать'' на произвольно искривленных фонах. Этого требуют задачи релятивистской астрофизики или космологии, где часто используются геометрии черных дыр или космологические решения, как заданные фоны.
(v) Может оказаться полезным обобщение на произвольные 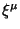$\xi^\mu$ , например, в работах [10] $^{\!, }$ [11] используются конформные векторы Киллинга космологического решения Фридмана, а не простые векторы Киллинга.
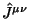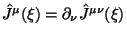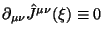(vi) Для сохраняющегося тока должен быть построен соответствующий антисимметричный суперпотенциал $\hat J^{\mu\nu}$ , так что $\hat J^\mu(\xi) = \partial_\nu \hat J^{\mu\nu} (\xi)$ и $\partial_{\mu\nu} \hat J^{\mu\nu} (\xi) \equiv 0$ . Становится очевидным дифференциальный закон сохранения, кроме того, сохраняющиеся интегралы естественным образом преобразуются в поверхностные.
(vii) Конечно, сконструированные законы и участвующие в них величины должны удовлетворять всем, так называемым, ,,естественным'' тестам. Это, как минимум:
- Положительность плотности энергии гравитационных волн;
- Правильное отношение массы к угловому моменту в решении Керра;
- Правильные значения глобальных интегралов для островной системы
на пространственной бесконечности,
на нулевой бесконечности.

Отметим, что пункт (vii) мы не будем подробно обсуждать в этих лекциях. При необходимости будем лишь отмечать удовлетворяет или нет обсуждаемая модель этим естественным тестам.

1.2.1 Законы сохранения Каца-Бичака-Линден-Белла

Кац, Бичак и Линден-Белл [12] (далее мы обозначаем эту работу как КБЛ) предложили такие законы сохранения, которые удовлетворяют предложенным требованиям. Построение основывается на лагранжиане

$\begin{displaymath} {\hat{\cal L}}_G = -{1\over 2\kappa} \left(\hat R - \overline {\hat R} + \partial_\mu \hat k^\mu \right). \end{displaymath}$

(1.27)

Здесь и далее используются обозначения: $g_{\mu\nu}$ - физическая метрика; $\bar g_{\mu\nu}$ - фоновая метрика с соответствующей ковариантной производной $\overline D_\mu$ ; черта сверху над символом везде означает фоновую величину;

$\hat R = \sqrt{-g} R$ и $\overline {\hat R} = \sqrt{-\bar g}\overline R$ ;

$\hat k^\mu = \hat g^{\mu\rho} \Delta^\sigma_{\rho\sigma} - \hat g^{\rho\sigma} \Delta^\mu_{\rho\sigma}$ , $\Delta^\mu_{\rho\sigma} = \Gamma^\mu_{\rho\sigma}- \overline{ \Gamma^\mu_{\rho\sigma}}$ .

Лагранжиан (1.27) обобщает для произвольных фонов известный ковариантный лагранжиан Розена на плоском фоне [13]. Если же $\bar g_{\mu\nu} \rightarrow \eta_{\mu\nu}$ , тогда $\overline D_\mu \rightarrow \partial_\mu$ и (1.27) переходит точно в эйнштейновсий усеченный лагранжиан (1.1).

Последовательное приложение процедуры Нетер к лагранжиану (1.27) с произвольным $\xi^\mu$ : ${\pounds_\xi} {\hat{\cal L}}_G + \partial_\mu \left(\xi^\mu {\hat{\cal L}}_G\right) \equiv 0$ дало возможность построить сохраняющийся ток $\hat J^\mu(\xi)$ и суперпотенциал $\hat J^{\mu\nu}(\xi)$ с соответствующим дифференциальным законом сохранения:

$\begin{displaymath} \partial_\mu \hat J^\mu (\xi) \equiv 0, \end{displaymath}$

(1.28)

$\begin{displaymath} \hat J^\mu(\xi) = \partial_\nu \hat J^{\mu\nu} (\xi). \end{displaymath}$

(1.29)

Поскольку (1.28) прямо следует из (1.29), то соотношения типа последнего мы часто также называем законами сохранения.

1.2.2 Суперпотенциал Каца-Крушциела

Суперпотенциалы играют очень важную роль в определении сохраняющихся величин. Дествительно, давайте подставим значение тока (1.29) в (1.26) и учтем антисимметрию $\hat J^{\mu\nu}(\xi)$ :

$\begin{displaymath} {\cal P}(\xi) = \int_{\Sigma} \hat J^0(\xi)d^3 x = \oint_{\partial\Sigma} \hat J^{0k}(\xi)ds_k, \end{displaymath}$

(1.30)

то есть мы получили, что сохраняющийся интеграл представляется в виде поверхностного интеграла по границе $\Sigma$ .

Суперпотенциал в выражении КБЛ (1.29) был получен раньше независимо Кацем [14] и Крушциелом [15]. Тогда он был построен для более простых систем, тем не менее более сложная модель разработанная КБЛ не изменила его вид:

$\begin{displaymath} {\hat J^{\mu\nu}(\xi)} ={1\over \kappa}\big({D^{[\mu}\hat \x... ...hat \xi^{\nu]}}\big)+ {1\over \kappa}\hat \xi^{[\mu} k^{\nu]}. \end{displaymath}$

(1.31)

Если $\bar g_{\mu\nu} \rightarrow \eta_{\mu\nu}$ , а вектор $\xi^{\mu}$ выбрать как киллинговский вектор трансляций в пространстве Минковского, то ${\hat J^{\mu\nu}(\xi)}$ переходит в суперпотенциал Фрейда (1.12).

1.2.3 Сохраняющийся ток КБЛ

Сохраняющаяся векторная плотность (ток КБЛ) в тождестве (1.28) имеет вид:

$\begin{displaymath} \hat J^\mu(\xi) = \hat \Theta^\mu_\nu \xi^\nu + \hat \sigma^{\mu\rho\sigma}\overline D_{\rho}\xi_{\sigma}+ \hat Z^\mu(\xi). \end{displaymath}$

(1.32)

Его структура следующая. Обобщенный тензор энергии-импульса имеет вид:

$\begin{displaymath} \hat \Theta^\mu_\nu = \left(\hat T^\mu_\nu - \overline {\hat... ...ight) \overline R_{\rho\sigma}\delta^\mu_\nu + \hat t^\mu_\nu, \end{displaymath}$

(1.33)

который тоже нужно описать по частям. Первое слагаемое представляет возмущение материального тензора энергии-импульса по отношению к фоновому, второе -- ,,потенциальное'' взаимодействие с фоновой геометрией, а третье есть тензор энергии-импульса гравитационного поля:

$\displaystyle 2\kappa \hat t^\mu_\nu$	=	$\displaystyle \hat g^{\rho\sigma} \left(\Delta^\lambda_{\rho\lambda} \Delta^\mu... ...mbda_{\lambda\nu} - 2\Delta^\mu_{\rho\lambda} \Delta^\lambda_{\sigma\nu}\right)$
	-	$\displaystyle \hat g^{\rho\sigma} \left(\Delta^\eta_{\rho\sigma} \Delta^\lambda... ...\rho_{\lambda\nu} - \Delta^\sigma_{\lambda\sigma} \Delta^\rho_{\rho\nu}\right).$	(1.34)

Если $\bar g_{\mu\nu} \rightarrow \eta_{\mu\nu}$ , то $\hat t^\mu_\nu$ переходит в псевдотензор Эйнштейна.

Второй член в (1.32) -- так называемый спиновый член:

$\displaystyle 2\kappa \hat \sigma^{\mu\rho\sigma}$	=	$\displaystyle (g^{\mu\rho} \overline g^{\sigma\nu} +\overline g^{\mu\sigma} g^{\rho\nu} - g^{\mu\nu} \overline g^{\rho\sigma})\hat \Delta^\lambda_{\nu\lambda}$
	-	$\displaystyle (g^{\nu\rho} \overline g^{\sigma\lambda} +\overline g^{\nu\sigma}... ...ambda} - g^{\nu\lambda} \overline g^{\rho\sigma}) \hat \Delta^\mu_{\nu\lambda}.$	(1.35)

Эта величина сама по себе также известна давно. Попытка построить сохраняющийся угловой момент с помощью псевдотензора Эйнштейна привела Папапетроу [16] к необходимости использовать выражение (1.35).

Структура последнего члена в (1.32) сложная и не так важна здесь, однако можно сказать, что $\hat Z^\mu(\xi)$ исчезает для киллинговых векторов фона.

Подведем некоторый итог. Величины КБЛ соответствуют всем сформулированным требованиям (i) - (vii). Это несомненное достоинство модели. Однако, вопрос единственности должен быть обсужден более подробно. Он может быть разделен на две части:

а) Насколько однозначен выбор лагранжиана (1.27)?

b) Насколько однозначны КБЛ величины при уже выбранном лагранжиане (1.27)?

Пункт а) детально обсуждался в работах [17] $^{\!, }$ [18]. Вывод такой, что требование использовать при варьировании граничные условия Дирихле единственным образом приводят к (1.27) и суперпотенциалу (1.31). Там же обсуждаются преимущества условий Дирихле. Независимо, развивая ковариантную Гамильтонову формулировку гравитационных теорий, к этому же выводу пришли авторы работы [19]. Слудующая часть лекции, c одной стороны, обобщает результаты КБЛ (в том смысле, что конструируются законы сохранения для произвольной полевой теории со вспомолательным фоном). Это позволяет ответить на вопрос пункта b). С другой стороны, результаты следующей части одновременно есть обобщение на произвольно искривленный фон результатов Мицкевича [8], который сконструировал сохраняющиеся величины для произвольной теории, но на плоском фоне.

<< 1.1 Классические псевдотензоры и ... | Оглавление | 1.3 Построение сохраняющихся токов ... >>

Публикации с ключевыми словами: законы сохранения - Общая теория относительности - гравитация
Публикации со словами: законы сохранения - Общая теория относительности - гравитация

См. также:

Галактика Арп 94

Спутники GRAIL составляют карту лунной гравитации

70 лет Стивену Хокингу

Молоток против перышка на Луне

Спутник Gravity Probe B подтвердил наличие гравимагнетизма

Что было до Большого взрыва и откуда взялось время?

Горячие черные дыры

Все публикации на ту же тему >>

Обсудить эту публикацию

Версия для печати

Астрометрия - Астрономические инструменты - Астрономическое образование - Астрофизика - История астрономии - Космонавтика, исследование космоса - Любительская астрономия - Планеты и Солнечная система - Солнце