Астронет > Динамические системы

по текстам по ключевым словам в глоссарии по сайтам перевод

Динамические системы

В. С. Анищенко

Саратовский государственный университет им. Н.Г. Чернышевского
Содержание

Колебательная система называется линейной или нелинейной в зависимости от того, линейна или нелинейна описывающая ее система дифференциальных уравнений. Линейные системы являются частным случаем нелинейных. Однако в силу принципиальной важности линейных систем при исследовании вопросов устойчивости колебаний, а также возможности использования принципа суперпозиции решений такая классификация оправданна.

Динамические системы, моделируемые конечным числом обыкновенных дифференциальных уравнений, называют сосредоточенными или точечными системами. Они описываются с помощью конечномерного фазового пространства и характеризуются конечным числом степеней свободы. Одна и та же система в различных условиях может рассматриваться либо как сосредоточенная, либо как распределенная. Математические модели распределенных систем — это дифференциальные уравнения в частных производных, интегральные уравнения или обыкновенные уравнения с запаздывающим аргументом. Число степеней свободы распределенной системы бесконечно, и требуется бесконечное число данных для определения ее состояния.

По энергетическому признаку динамические системы делятся на консервативные и неконсервативные. Консервативные системы характеризуются неизменным во времени запасом энергии. В механике их называют гамильтоновыми. Для консервативных систем с n степенями свободы определяется гамильтониан системы H(p, q), где q_i — обобщенные координаты, p_i — обобщенные импульсы системы, i = 1, 2, ..., n. Гамильтониан полностью характеризует динамическую природу системы и с физической точки зрения в большинстве случаев представляет собой ее полную энергию. Эволюция во времени консервативных систем описывается уравнениями механики Гамильтона

$$\dot q_i = \frac{\partial \bf H\rm (\bf p\rm , \bf q\rm )}{\partial p_i}$,$ $\dot p_i = -\frac{\partial \bf H \rm (\bf p\rm , \bf q\rm )}{\partial q_i}.$ (9)

Динамические системы с изменяющимся во времени запасом энергии называются неконсервативными. Системы, в которых энергия уменьшается во времени из-за трения или рассеяния, называются диссипативными. В соответствии с этим системы, энергия которых во времени нарастает, называются системами с отрицательным трением или отрицательной диссипацией. Такие системы можно рассматривать как диссипативные при смене направления отсчета времени на противоположное.

Динамические системы называются автономными, если они не подвержены действию внешних сил, переменных во времени. Уравнения автономных систем явной зависимости от времени не содержат. Большинство реальных колебательных систем в физике, радиофизике, биологии, химии и других областях знаний неконсервативны. Среди них выделяется особый класс автоколебательных систем, которые принципиально неконсервативны и нелинейны. Автоколебательной называют динамическую систему, преобразующую энергию источника в энергию незатухающих колебаний, причем основные характеристики колебаний (амплитуда, частота, форма колебаний и т.д.) определяются параметрами системы и в определенных пределах не зависят от выбора исходного начального состояния.

Фазовые портреты типичных колебательных систем

Геометрическое представление колебаний. Метод анализа колебательных процессов с помощью исследования фазовых траекторий динамической системы был введен в теорию колебаний Л.И. Мандельштамом и А.А. Андроновым и с тех пор стал привычным при исследовании различных колебательных явлений. Обсудим несколько простых, но типичных примеров представления динамических процессов в виде траекторий изображающей точки в фазовом пространстве.

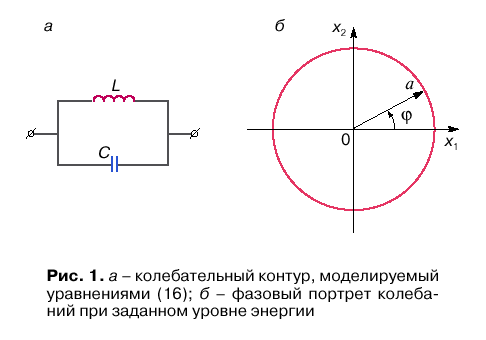
Консервативный осциллятор. Рассмотрим линейный осциллятор без потерь, уравнения которого можно сформулировать на примере колебательного LC-контура (рис. 1, а), предположив амплитуду колебаний достаточно малой. Выбрав в качестве переменной заряд q на конденсаторе, с помощью уравнений Кирхгофа получим

$\ddot q +(LC)^{-1}q = 0.$ (10)

Домножив (10) на $L\dot q$ , получаем

$\frac{d}{dt}\biggl( \frac{L\dot q^2}{2} + \frac{q^2}{2C} \biggr) = 0,$ (11)

то есть для любого момента времени выполняются равенства

$E = E_L + E_C = const, E_L = \frac{L\dot q^2}{2}, E_C = \frac{q^2}{2C},$ (12)

отражающие постоянство во времени полной энергии осциллятора (суммы магнитной E_L и электрической E_C энергий). В более удобных координатах уравнения консервативного осциллятора можно записать следующим образом, введя замену времени $\tau = t/\sqrt{LC}$ и обозначая для общности q через x :

$\ddot x + x = 0,$ $\dot x^2 + x^2 = a^2,$ $a = const .$ (13)

Для фазовых координат $x_1 = x$ и $x_2 = \dot x$ эти уравнения преобразуются к виду

$\dot x_1 = x_2,$ $\dot x_2 = - x_1,$ $x_1^2 + x_2^2 = a^2.$ (14)

Фазовый портрет системы представляет собой окружность радиуса a с центром в начале координат. Точка в фазовом пространстве, в которой вектор фазовой скорости обращается в нуль, называется особой, и в данном случае нуль координат есть особая точка типа центр.

Наличие интеграла движения у рассматриваемой системы, отражающее факт сохранения энергии (12), дает возможность описать ее с помощью уравнения 1-го порядка. Действительно, определив новую переменную $\phi$ соотношениями

$x_1 = a \sin \phi ,$ $x_2 = a \cos \phi ,$ (15)

получим уравнения

$\dot \phi = 1,$ $\dot a = 0,$ (16)

которые и представляют закон движения фазовой точки. Во времени эволюционирует одна переменная $\phi$ , и фазовое пространство консервативного осциллятора, таким образом, одномерно. Гармоническим колебаниям осциллятора отвечает равномерное движение изображающей точки по окружности радиуса a, как это показано на рис. 1, б.

Если консервативная система нелинейна, то ее фазовый портрет усложняется. Проиллюстрируем это на примере уравнения

$\ddot x + \sin x = 0.$ (17)

В фазовых переменных $x_1 = x$ , $x_2 = \dot x$ это уравнение сводится к следующим:

$\dot x_1 = x_2,$ $\dot x_2 = -\sin x_1.$ (18)

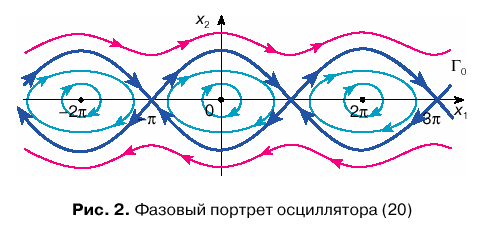
Состояния равновесия нелинейного маятника на фазовой плоскости расположены вдоль оси x₁ (x₂ = 0) в точках $x_1 = 0, \pm \pi, \pm 2\pi, ...$ Соответствующий фазовый портрет системы представлен на рис. 2. Видно, что особые точки $x_1 = 0, \pm 2\pi, \pm 4\pi, ...$ типа центр, а $x_1 = 0, \pm \pi, \pm 3\pi, ...$ — неустойчивые точки типа седло.

Вблизи центров фазовый портрет соответствует линейному осциллятору: траектории представляют собой замкнутые кривые, близкие к окружностям, что отвечает по амплитуде колебаниям, близким к гармоническим. Через неустойчивые точки проходят особые интегральные кривые $\Gamma_0$ , называемые сепаратрисами. Они разделяют фазовое пространство на области с различным поведением. С увеличением энергии маятника его колебания от квазигармонических вблизи точек типа центр эволюционируют к нелинейным периодическим колебаниям вблизи сепаратрис. Дальнейшее увеличение энергии приведет к вращательному движению (движение вне сепаратрис). Малейшие отклонения энергии в ту или иную сторону от энергии движения по сепаратрисе приводят к качественно различным типам движения: колебательному или вращательному.

Линейный осциллятор с затуханием. Диссипация энергии, обусловленная наличием потерь, оказывает принципиальное влияние на характер движения системы. Наиболее простые закономерности проявляются в системах с полной диссипацией энергии, когда силы трения действуют по всем степеням свободы, а поступление энергии извне отсутствует. Рассмотрим процессы в линейном диссипативном осцилляторе, когда сила трения пропорциональна скорости изменения координаты. Примером такой системы служит колебательный контур, содержащий активное сопротивление R. Уравнение контура

$L\ddot q + R\dot q + \frac{q}{C} = 0$ (19)

заменой переменных сводится к безразмерной форме

$\ddot x + \delta \dot x +x = 0,$ $2\delta = R\sqrt{\frac{L}{C}},$ $\tau = \frac{t}{\sqrt{LC}}$ (20)

При d = 0 имеем консервативный линейный осциллятор, рассмотренный выше. Введение малого трения качественно меняет фазовый портрет системы. Для 0 < d < 1 решением уравнения (20) является

$x = A \exp (-\delta t) \cos (\omega \tau + \psi),$ $\omega = (1 - \delta^2)^{1/2},$ (21)

где A и $\psi$ — произвольные постоянные, определяемые начальными условиями. На фазовой плоскости для любых начальных данных имеют место скручивающиеся спирали, по которым фазовые точки асимптотически приближаются к началу координат, характеризуя затухающий колебательный процесс. Нуль координат является особой точкой системы, которая в случае d < 1 есть устойчивый фокус (рис. 3, а). Если коэффициент трения d > 1, процесс в системе апериодический:

$x = A_1 \exp (\lambda_1 \tau) + A_2 \exp (\lambda_2 \tau),$
$\lambda_{1, 2} = [- \delta \pm (\delta^2 - 1)^{1/2}]/2$ (22)

и фазовые траектории выглядят как семейство характерных кривых, по которым, как и в предыдущем случае, изображающие точки стремятся к нулю координат (рис. 3, б). Особая точка в указанных условиях является устойчивым узлом.

Итак, при любых значениях физических параметров системы, когда $\delta > 0$ , диссипативный маятник характеризуется единственным глобально устойчивым состоянием равновесия в нуле фазовых координат. Независимо от выбора начальных условий наблюдается затухающее колебательное или апериодическое движение. При $t \to \infty$ любая (!) изображающая точка стремится к началу координат в устойчивый фокус либо узел.

Описанное свойство является общим для динамических систем с полной диссипацией энергии. Положения равновесия типа устойчивого фокуса или узла являются здесь глобально притягивающими в том смысле, что фазовые траектории из любой точки фазового пространства асимптотически к ним стремятся. Стационарные незатухающие колебания в линейных диссипативных системах оказываются невозможными. С физической точки зрения это понятно — нет условий поддержания колебаний. Энергия, расходуемая на преодоление сил трения, не восполняется.

Назад | Вперед

Публикации с ключевыми словами: хаос Публикации со словами: хаос
См. также: хаос Введение в физику открытых систем

Обсудить эту публикацию

Версия для печати

Астрометрия - Астрономические инструменты - Астрономическое образование - Астрофизика - История астрономии - Космонавтика, исследование космоса - Любительская астрономия - Планеты и Солнечная система - Солнце