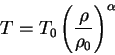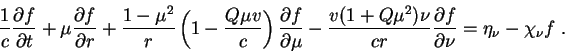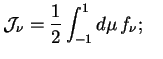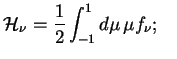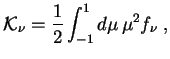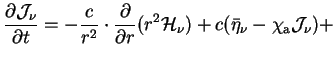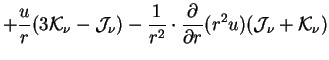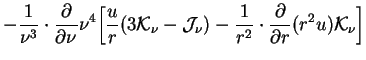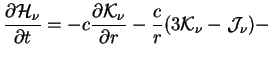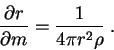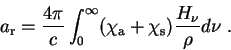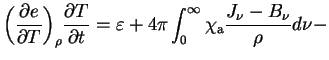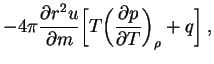Теоретический каталог сверхновых второго типа
<< Введение. Теоретический каталог | Оглавление | 2. Результаты моделирования >>
1. Моделирование взрыва.
Сверхновая рассматривается как взрыв некоторого равновесного газового
шара, для которого строится конфигурация(называемая в дальнейшем предсверхновая)
с заранее предписанным распределением
химического состава с заданной массой и радиусом в гидростатическом
равновесии. В результате получаем распределение давления,
температуры и плотности по радиусу. Затем вносим (немалое!)
начальное возмущение в центральных зонах этого шара, выделяем
тепловую или кинетическую энергию порядка наблюдаемой кинетической
энергии взрыва сверхновой. Конечно, начальная энергия должна быть
несколько выше, так как заметная часть уходит на преодоление
самогравитации, а какой-то процент уходит в излучение фотонов (тем
больший, чем больше начальный радиус, так как чем ниже плотность,
тем больше доля энтропии порожденной ударной волной переходит к
фотонному газу).
1.1 Предсверхновая.
Что значит создание предсверхновой?
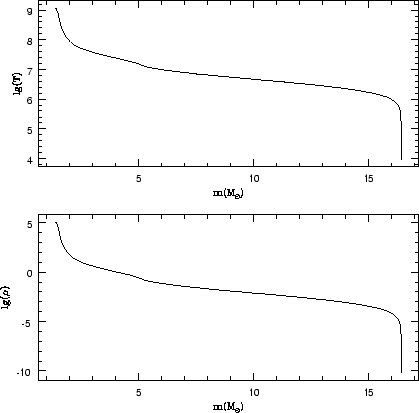
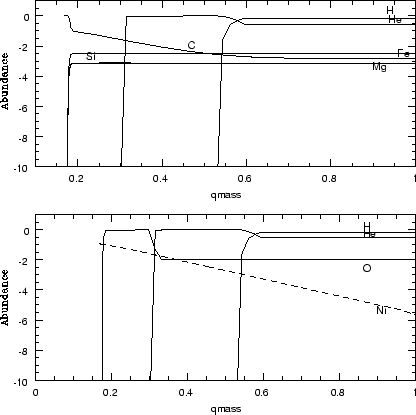
Создание предсверхновой -- это расчет равновесного газового шара, поделенного на 100 сферически-симметричных зон, в пределах которых считалось действует приближение ЛТР. Для газового шара задавали глобальные параметры, как масса, радиус, хим. состав. Распределение элементов по звезде близко к результатам эволюционного моделирования и приведено на рис.(1.1)
 |
Использовались еще менее значительные параметры, например, плотность на границе звезды и др., которые при моделировании не менялись.
Из решения уравнения гидростатического равновесия
выводились зависимости между
![]() .
.
Между температурай и плотностью принималось политропное соотношение:
Затем численно рассчитывались значения T, ![]() , P в каждой зоне в
приближении идеального газа, но с полным учетом ионизации по Саха.
Зависимость между
, P в каждой зоне в
приближении идеального газа, но с полным учетом ионизации по Саха.
Зависимость между ![]() и
и ![]() показана на
рис. 1.2.
показана на
рис. 1.2.
Модель предсверхновой можно представить, как таблицу:
по вертикали задаются слои(зоны) в предсверхновой
по горизонтали -- параметры предсверхновой в этой зоне( T, ![]() , P и др.)
, P и др.)
Ниже дан пример: первые шесть строк из таблицы для предсверхновой r500m3ni2 с
![]() ,
,
![]()
| zone | mass | ... | |||
| 1 | 1.414 | 8.853 | 9.030 | 4.894 | ... |
| 2 | 1.419 | 8.866 | 9.017 | 4.856 | ... |
| 3 | 1.426 | 8.883 | 9.001 | 4.807 | ... |
| 4 | 1.434 | 8.905 | 8.979 | 4.743 | ... |
| 5 | 1.446 | 8.934 | 8.951 | 4.658 | ... |
| 6 | 1.460 | 8.973 | 8.913 | 4.543 | ... |
| ... | ... | ... | ... | ... | ... |
1.2 Расчет непрозрачности.
Следующим шагом, приближающим нас собственно к самому взрыву, был
расчет непрозрачности. Достаточно длительный и утомительнй для
ЭВМ процесс. В каждой из ста зон для каждого из ста интервалов
частот считалась полная непрозрачность вещества.
В полную непрозрачность были включены эффекты фотоионизации, свободно-свободного
поглощения, линии и электронное рассеяние. Учтено было
![]() линий
в диапазоне
от
линий
в диапазоне
от ![]() до
до ![]() по данным Kurucz R.L. 1991.
Исчерпывающую информацию по расчету непрозрачности в пакете STELLA см.([1]).
по данным Kurucz R.L. 1991.
Исчерпывающую информацию по расчету непрозрачности в пакете STELLA см.([1]).
При расчете непрозрачности считалось:
1) при взрыве вещество не перетекает из зоны в зону,
2) хим. состав в каждой зоне при изменении радиуса предсверхновой
постоянен,
3) непрозрачность не зависит от энергии взрыва.
При таких предположениях можно расчитать только
четыре таблицы непрозрачности: для каждой массы(5.77, 8.41, 16.41, 20.41 ![]() ).
И использовать их при расчете вспышки для соответствующей массы.
Такой подход дал возможность рассчитать большее число моделей.
).
И использовать их при расчете вспышки для соответствующей массы.
Такой подход дал возможность рассчитать большее число моделей.
1.3 Расчет взрыва сверхновой.
Получив таблицы непрозрачности и модель предсверхновой, стало возможным, приступать к взрыву звезды. Расчет взрыва сверхновой в программе STELLA проводился по следующей схеме (см. также [1]).
Запишем уравнение Больцмана в сопутствующей системе отсчета для галилеевского приближения
(эффекты ![]() не учитываются) в сферически-симметричном случае :
не учитываются) в сферически-симметричном случае :
И введем угловые моменты функции распределения ![]() :
:
То следуя [1], получим уравнения в сопутствующей системе, в том виде как они используются в программе (частная производная по времени берется при фиксированной лагранжевой координате). После интегрирования (1.2) по
Интегрирование (1.2) по
плюс еще несколько членов, которыми можно пренебречь Здесь
Уравнения (1.4) и (1.5) для всех частот (то есть для всех частотных групп) решаются одновременно с уравнениями гидродинамики в лагранжевых координатах:
Здесь
Необходимое уравнение для температуры вещества ![]() , можно
получить из первого начала термодинамики с помощью
(1.6), (1.8) и термодинамического тождества:
, можно
получить из первого начала термодинамики с помощью
(1.6), (1.8) и термодинамического тождества:
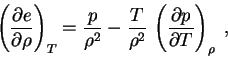 |
(1.10) |
Здесь
Понятно, что для замыкания системы
надо избавиться от
момента ![]() . Принимается, что
. Принимается, что
В качестве граничных условий
полагается, что на внешней границе (![]() , где
, где ![]() - полная
масса звезды) давление вещества пренебрежимо мало:
- полная
масса звезды) давление вещества пренебрежимо мало:
Все производные по пространству и частоте в
уравнениях заменяются на конечные разности. При этом необходимо проявлять
аккуратность и осторожность при усреднении величин с большими скачками
между соседними зонами, при переходе от оптически тонких к оптически
толстым зонам, при сшивке зон с полным расчетом переноса с зонами, где
излучение описывается в приближении диффузии равновесного излучения.
Для каждой искомой величины в каждой расчетной ячейке
можно теперь трактовать частные производные по времени как полные.
Таким образом, получается система
обыкновенных дифференциальных уравнений (ОДУ) для эволюции ![]() ,
, ![]() ,
, ![]() в каждой лагранжевой зоне, а для
в каждой лагранжевой зоне, а для ![]() и
и ![]() еще и
в каждой группе по частоте.
Это хорошо известный метод линий, или прямых,
который в данном случае дает до
еще и
в каждой группе по частоте.
Это хорошо известный метод линий, или прямых,
который в данном случае дает до
![]() ОДУ, т.е.
до нескольких десятков тысяч уравнений.
Для интегрирования этой огромной
системы используется неявный метод прогноза и коррекции высокого порядка по времени, основанный на методах Гира и
Брайтона и др. , с автоматическим выбором порядка и
шага по времени.
ОДУ, т.е.
до нескольких десятков тысяч уравнений.
Для интегрирования этой огромной
системы используется неявный метод прогноза и коррекции высокого порядка по времени, основанный на методах Гира и
Брайтона и др. , с автоматическим выбором порядка и
шага по времени.
<< Введение. Теоретический каталог | Оглавление | 2. Результаты моделирования >>
|
Публикации с ключевыми словами:
Сверхновые - кривая блеска
Публикации со словами: Сверхновые - кривая блеска | |
См. также:
Все публикации на ту же тему >> | |