<< 3. Волны Россби в диске | Оглавление | 5. Эффекты Россби на Солнце >>
4. Волны Россби в массивных
протозвездных облаках
1![]() . Наблюдения показывают, что в ряде массивных
протозвездных облаков формируются одновременно несколько молодых
звездных объектов. При этом закономерностью является то, что
коллимированные сверхзвуковые струйные выбросы из этих объектов
ориентированы под очень малым углом друг к другу в каждом облаке.
На наш взгляд, это однозначно указывает на то, что за их
формирование ответствен единый универсальный волновой механизм,
приводящий к образованию регулярных структур в облаке.
. Наблюдения показывают, что в ряде массивных
протозвездных облаков формируются одновременно несколько молодых
звездных объектов. При этом закономерностью является то, что
коллимированные сверхзвуковые струйные выбросы из этих объектов
ориентированы под очень малым углом друг к другу в каждом облаке.
На наш взгляд, это однозначно указывает на то, что за их
формирование ответствен единый универсальный волновой механизм,
приводящий к образованию регулярных структур в облаке.
Для прояснения причин формирования почти параллельных
струйных выбросов из молодых звездных объектов, находящихся в
одном протозвездном облаке, необходимо прежде всего определить
причину возникновения у них квазипараллельных моментов вращения,
поскольку молодые звезды представляют собой аккреционно-струйные
системы, в которых джеты распространяются всегда вдоль оси
вращения околозвездного диска [1-3]. Такой причиной может быть
эффект, обусловленный действием силы Кориолиса - волны Россби
[4], а впоследствии - формирование долгоживущих вихрей Россби,
хорошо исследованных в геофизике и физике планетных атмосфер (см.
[5-7], там же ссылки на оригинальные работы).
Рассматриваемая нами ситуация значительно отличается от обсуждаемых в [5-7] принципиальной необходимостью учета самогравитации, поскольку характерная длина волны Джинса в любом случае много меньше характерного масштаба облака, иначе не происходили бы его гравитационный коллапс и уж тем более образование нескольких молодых звезд в этом облаке.
|
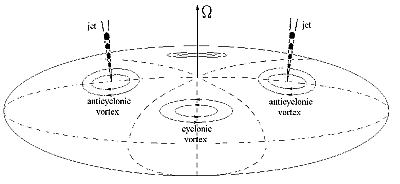
Рис. 2. Схематическое изображение развития циклонических и антициклонических вихрей Россби в некотором слое вращающегося массивного протозвездного облака |
- после инициирующего процесса, которым может быть, например,
прохождение холодным газовым облаком фронта галактической ударной
волны, джинсовский масштаб становится меньше характерного масштаба
облака и начинается гравитационное сжатие последнего;
- наличие начального суммарного момента импульса приводит к
вращению облака, все убыстряющемуся по мере сжатия;
- центробежные эффекты приводят к тому, что сжатие
вдоль оси вращения происходит быстрее, чем в поперечной плоскости,
из-за чего облако принимает форму сплюснутого эллипсоида вращения;
- при достижении определенной скорости вращения облака число
Кибеля-Россби оказывается достаточно малым для появления в
облаке волн и вихрей Россби;
- в высоких широтах формируется регулярная структура циклонических
и антициклонических вихрей;
- из-за повышения плотности в антициклонах джинсовский масштаб
локально оказывается для них меньше, чем для окружающей среды и
соответственно развивается локальная гравитационная
неустойчивость;
- развитие последней приводит к образованию протозвезд с
антициклоническими роторами скоростей, образующими друг с другом малые
углы;
- на определенной стадии эволюции протозвезд в силу общих закономерностей, которые мы обсуждали в [1-3], в протозвездах формируются джеты, параллельные их собственным моментам вращения, и реализуется ситуация, показанная на рис. 2 (при этом, вероятно, сквозь облако будет просвечивать центральное ядро, значительно разогретое гравитационным сжатием).
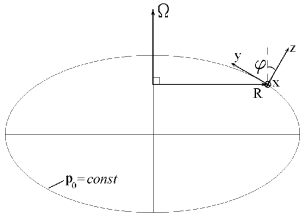
3![]() . Для исследования закона дисперсии возмущений
малой амплитуды рассмотрим протозвездное облако, обладающее неким
суммарным моментом вращения на стадии гравитационного сжатия,
из-за чего его изобары представляют собой эллипсоиды вращения.
Такая конфигурация безусловно нестационарна; мы, однако,
предполагаем, что характерное время сжатия значительно превышает
период вращения облака. Основания надеятся на это дает тот факт,
что протозвездные облака богаты металлической пылью и
соответственно обладают большой оптической толщей и большим
временем выхода излучения. Поэтому вероятнее всего коллапс такого
облака будет происходить не монотонно во времени, а в пульсирующем
режиме, во время одной стадии которого будет происходить разогрев
центральных областей при практически адиабатическом гравитационном
сжатии облака, из-за чего в этих областях увеличится джинсовский
масштаб и сжатие замедлится, а на второй стадии система будет
ожидать, когда излишек энергии будет унесен излучением и
джинсовский масштаб уменьшится.
. Для исследования закона дисперсии возмущений
малой амплитуды рассмотрим протозвездное облако, обладающее неким
суммарным моментом вращения на стадии гравитационного сжатия,
из-за чего его изобары представляют собой эллипсоиды вращения.
Такая конфигурация безусловно нестационарна; мы, однако,
предполагаем, что характерное время сжатия значительно превышает
период вращения облака. Основания надеятся на это дает тот факт,
что протозвездные облака богаты металлической пылью и
соответственно обладают большой оптической толщей и большим
временем выхода излучения. Поэтому вероятнее всего коллапс такого
облака будет происходить не монотонно во времени, а в пульсирующем
режиме, во время одной стадии которого будет происходить разогрев
центральных областей при практически адиабатическом гравитационном
сжатии облака, из-за чего в этих областях увеличится джинсовский
масштаб и сжатие замедлится, а на второй стадии система будет
ожидать, когда излишек энергии будет унесен излучением и
джинсовский масштаб уменьшится.
В силу сказанного данная часть нашей работы не может претендовать на математическую строгость, достаточно корректно рассматриваемая задача может быть решена лишь методом эволюционного численного нелинейного моделирования; основная цель настоящей заметки - проанализировать, имеются ли предпосылки для постановки такого моделирования.
Среду моделируем невязким сжимаемым самогравитирующим
идеальным газом с уравнением состояния

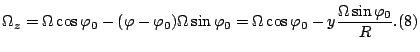

Будем рассматривать динамику баротропных возмущений, не имеющих
![]() -структуры (в отличие от бароклинных - см. [6]), поскольку
нас интересуют наиболее крупномасштабные возмущения. Формальное
основание для такой постановки задачи дает тот факт, что
вертикальный масштаб изменения «равновесной» плотности облака
для степенных распределений параметров модели
-структуры (в отличие от бароклинных - см. [6]), поскольку
нас интересуют наиболее крупномасштабные возмущения. Формальное
основание для такой постановки задачи дает тот факт, что
вертикальный масштаб изменения «равновесной» плотности облака
для степенных распределений параметров модели
В такой постановке задачи динамика малых возмущений вида
![]() определяется системой
линеаризованных уравнений:
определяется системой
линеаризованных уравнений:
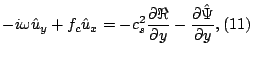
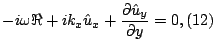

Дифференцируя (11) по ![]() , исключаем из (10) и (11)
, исключаем из (10) и (11) ![]() и
и
![]() при помощи (13) и (12) соответственно; получаем
при помощи (13) и (12) соответственно; получаем

С другой стороны, дифференцируя (10) по ![]() , исключаем
, исключаем ![]() и
и
![]() при помощи (12):
при помощи (12):

Предполагая далее возмущения достаточно коротковолновыми вдоль меридиана
(
![]() ), ищем решение в виде
), ищем решение в виде
![]() и, выписывая условие совместности уравнений (14) и (15), получаем
дисперсионное
уравнение с точностью до линейных по малому параметру
и, выписывая условие совместности уравнений (14) и (15), получаем
дисперсионное
уравнение с точностью до линейных по малому параметру
![]() слагаемых:
слагаемых:
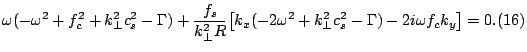
Отметим, что последнее слагаемое в квадратных скобках в (16) является нефизичным, и его необходимо просто отбросить. Действительно, появление в дисперсионном уравнении физичных мнимых слагаемых возможно только в задачах с диссипацией или внешней накачкой энергии. В данном же случае это является следствием не вполне корректного учета геометрии задачи: реально расстояние между меридианами уменьшается с приближением к полюсу, из-за чего, в силу сохранения потока энергии в волне, ее амплитуда должна при этом возрастать, что не учитывается в нашей приближенной постановке задачи.
Однако даже с учетом сделанного замечания в предельном случае
несамогравитирующей среды (
![]() ) уравнение (16) не
переходит в классический закон дисперсии волн Россби и
гравитационно-гироскопических волн [5-7], отличаясь слагаемым
) уравнение (16) не
переходит в классический закон дисперсии волн Россби и
гравитационно-гироскопических волн [5-7], отличаясь слагаемым
![]() в последней скобке. Это не удивительно, поскольку
(16) получено из уравнений более высокого порядка. Тем не менее
численное исследование показывает, что это слагаемое в указанном
предельном случае дает поправку второго порядка малости как к
частоте гравитационно-гироскопических волн, так и к частоте волн
Россби.
в последней скобке. Это не удивительно, поскольку
(16) получено из уравнений более высокого порядка. Тем не менее
численное исследование показывает, что это слагаемое в указанном
предельном случае дает поправку второго порядка малости как к
частоте гравитационно-гироскопических волн, так и к частоте волн
Россби.
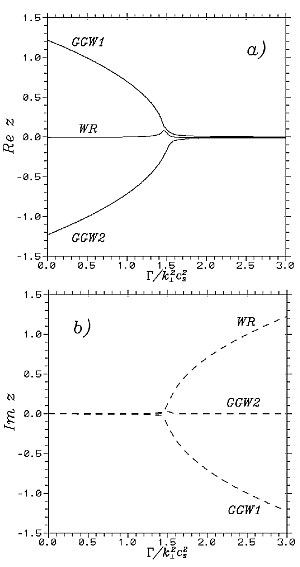 |
Рис. 4.
Зависимости относительных фазовых скоростей
|
4![]() . На рис. 4 мы приводим дисперсионные кривые
в зависимости от квадрата
отношения длины волны возмущений к джинсовскому масштабу
(
. На рис. 4 мы приводим дисперсионные кривые
в зависимости от квадрата
отношения длины волны возмущений к джинсовскому масштабу
(
![]() ).
).
Наиболее важными для нашего рассмотрения в полученных результатах являются два момента. Во-первых, если гравитационно-гироскопические волны (акустическая мода колебаний) при превышении критического масштаба Джинса оказываются либо слабо неустойчивыми, либо затухают, то волны Россби (вихревая мода колебаний) обладают значительной относительной скоростью роста амплитуды. Во-вторых, эта скорость роста оказывается сравнимой со скоростью звука и существенно превышает фазовую скорость волн Россби. В то же время в [5] показано, что скорость дрейфа нелинейного пакета антициклонических волн Россби приближается к их фазовой скорости, определенной на основе линейного анализа. Таким образом, плотность в антициклонических вихрях Россби должна нарастать из-за эффектов самогравитации значительно быстрее, чем они будут смещаться вдоль широты из-за дрейфа.
 |
Рис. 5.
Линии уровней относительных скоростей роста амплитуды
|
К аналогичному выводу позволяют прийти и наши исследования. Как следует из рис. 5, определяющая скорость дрейфа групповая скорость для волн Россби меньше или сравнима с фазовой скоростью этих волн и, следовательно, много меньше как звуковой скорости, так и скорости роста амплитуды из-за развития гравитационной неустойчивости.
Априорно ясно, что столь быстрое развитие гравитационной
неустойчивости в локальных антициклонических уплотнениях
очень
быстро приведет к нарушению режима Россби: число
Кибеля-Россби перестанет быть малым - из-за тенденции к
сохранению углового момента в вихрях уменьшающегося со временем
радиуса и соответственно раскручивающихся. Тем не менее,
представляется вполне вероятным, что такие структуры окажутся
долгоживущими (именно в силу указанной тенденции) и приведут к
образованию протозвезд и формированию джетов.
Обобщая проведенный анализ, можно, вероятно, утверждать, что любое газовое облако, испытывающее гравитационный коллапс, с неизбежностью проходит стадию режима Россби, если только его суммарный начальный момент импульса не равен нулю. Как представляется, сопутствующее этому процессу возникновение значительных неоднородностей необходимо учитывать при рассмотрении эволюции астрофизических объектов.
<< 3. Волны Россби в диске | Оглавление | 5. Эффекты Россби на Солнце >>