Зеемана эффект
- расщепление спектральных линий под действием на излучающее вещество внеш. магн. поля. 3. э., наблюдаемый в спектрах поглощения, получил название обратного, все его закономерности аналогичны закономерностям прямого 3. э. (наблюдаемого в линиях излучения). 3. э. был открыт нидерландским физиком П. Зееманом в 1896 г. при лабораторных исследованиях свечения паров натрия.
|
|
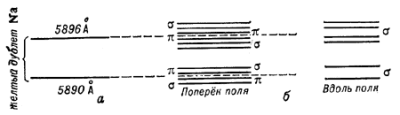
Рис. 1. Картина расщепления двух близких спектральных линий атома натрия (жёлтого дублета Na) в магнитном поле при наблюдении поперёк и вдоль поля; поляризованы различно. |
|
|
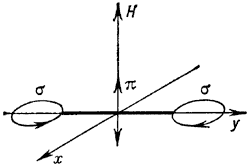
Рис. 2. Поляризация (поперечный эффект Зеемана) и - направление магнитного поля, плоскость x, y - плоскость поляризации |
Первое объяснение 3. э. было дано нидерл. физиком Х. Лоренцем в 1897 г. в рамках классич. теории, согласно к-рой движение электрона в атоме рассматривается как гармония, колебания линейного осциллятора. По этой теории спектр. линия при поперечном 3. э. расщепляется на три компонента. Такое явление получило название нормального 3. э., а расщепление линии на большее число компонентов - аномального З.э. Однако обычно наблюдается именно аномальный эффект. Исключение составляют переходы между синглетными уровнями, а также случаи сильного магн. поля (см. ниже).
Полное объяснение 3. э. получил на основе квантовой теории. Уровни энергии атома расщепляются в магн. поле на подуровни. Квантовые
переходы между подуровнями двух уровней порождают компоненты спектр. линии. Каждый
энергетич. уровень атома характеризуется механич. моментом количества движения J.
Расщепление уровней обусловлено тем, что с механич. моментом связан магн. момент
![]() J,
J, ![]() , (1)
, (1)
где e, m - заряд и масса электрона, (![]() - магнетон Бора, a g
- т.н. фактор Ланде. Смысл разделения коэфф. на два множителя поясняется ниже. Знак
минус обусловлен отрицат. зарядом электрона. Взаимодействие магнитного момента
- магнетон Бора, a g
- т.н. фактор Ланде. Смысл разделения коэфф. на два множителя поясняется ниже. Знак
минус обусловлен отрицат. зарядом электрона. Взаимодействие магнитного момента ![]() с полем H изменяет энергию уровня. Величина этого взаимодействия
зависит от взаимной ориентации
с полем H изменяет энергию уровня. Величина этого взаимодействия
зависит от взаимной ориентации ![]() и H. Вектор J
в магн. поле может иметь 2J+1 ориентации, при к-рых его проекция JH=M,
где М - магнитное квантовое число. Оно принимает значения 0,
и H. Вектор J
в магн. поле может иметь 2J+1 ориентации, при к-рых его проекция JH=M,
где М - магнитное квантовое число. Оно принимает значения 0, ![]() . Столько же значений может иметь проекция
. Столько же значений может иметь проекция ![]() магн. момента
магн. момента
![]() на направление H. Поэтому уровень расщепляется на
2J+1 компонентов. Изменение энергии
на направление H. Поэтому уровень расщепляется на
2J+1 компонентов. Изменение энергии ![]() каждого
компонента
(по отношению к энергии уровня в отсутствие поля) с учётом ф-лы (1) равно:
каждого
компонента
(по отношению к энергии уровня в отсутствие поля) с учётом ф-лы (1) равно:
![]() . (2)
. (2)
Механич. момент атома складывается из орбитального момента L и спинового
момента S: J=L+S. Аналогично магн. момент ![]() .
Величина
.
Величина ![]() подобна магн. моменту тока, образованного орбитальным
движением электронов в атоме, и равна
подобна магн. моменту тока, образованного орбитальным
движением электронов в атоме, и равна ![]() L. С величиной
L. С величиной
![]() дело обстоит сложнее, т.к. спиновый момент S связан с внутр. характеристикой
электронов, а не с их движением. Как следует из эксперимента (а также из релятивистской
квантовой теории Дирака),
дело обстоит сложнее, т.к. спиновый момент S связан с внутр. характеристикой
электронов, а не с их движением. Как следует из эксперимента (а также из релятивистской
квантовой теории Дирака), ![]() S, т.е. на единицу
спинового момента приходится вдвое больший магн. момент. Т.о., полный магн. момент
S, т.е. на единицу
спинового момента приходится вдвое больший магн. момент. Т.о., полный магн. момент
![]() (L+2S)=
(L+2S)=![]() (J+S).
(3)
(J+S).
(3)
Вектор ![]() прецессирует вокруг вектора J, так что в среднем
он направлен вдоль J, а его величина определяется по ф-ле (1). Согласно
расчётам на основе квантовой механики, фактор Ланде
прецессирует вокруг вектора J, так что в среднем
он направлен вдоль J, а его величина определяется по ф-ле (1). Согласно
расчётам на основе квантовой механики, фактор Ланде
g=1+[J(J+1)-L(L+1)+S(S+1)]/2J(J+1). (4)
|
|
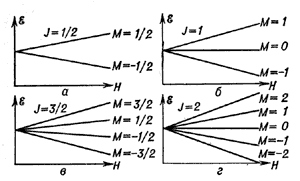
Рис. 3. Зависимость расщепления уровней энергии от напряжённости магнитного поля: а - при J=1/2, б - при J= 1, в - при J=3/2, г - при J= 2, M - магнитное квантовое число. |
Изменение квантового числа М определяется правилом отбора
В очень сильном поле H связь L и S нарушается,
оба вектора начинают независимо друг от друга прецессировать вокруг направления J
с проекциями ML и MS.
Нарушение связи имеет место в случае, когда зеемановское расщепление становится больше
тонкой структуры, т.е. J-структуры уровня LS. При этом ![]() .
Правило отбора для
.
Правило отбора для ![]() такое же, как для
такое же, как для ![]() , а
, а ![]() = 0. Поэтому
= 0. Поэтому ![]() и опять проявляется норм. 3. э. В данных условиях каждый зеемановский компонент
имеет тонкую структуру (подобно J-структуре уровня LS). Компоненты
этой структуры характеризуются значением величины
и опять проявляется норм. 3. э. В данных условиях каждый зеемановский компонент
имеет тонкую структуру (подобно J-структуре уровня LS). Компоненты
этой структуры характеризуются значением величины ![]() . Переход
от аномального
к нормальному 3. э. в сильном поле наз. эффектом Пашена-Бака. При переходе нарушается
линейная зависимость смещения от поля. Для различных линий эффект возникает при разных
величинах магн. поля.
. Переход
от аномального
к нормальному 3. э. в сильном поле наз. эффектом Пашена-Бака. При переходе нарушается
линейная зависимость смещения от поля. Для различных линий эффект возникает при разных
величинах магн. поля.
В астрофизике 3. э. используется для определения магн. полей космич. объектов.
|
|
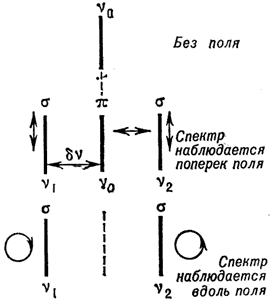
Рис. 4. Нормальный эффект Зеемана; стрелками обозначена поляризация компонентов, линии, частоты |
При измерениях магн. полей звёзд зеемановское расщепление спектр. линий обычно наблюдается
в поглощении. Продольный компонент магн. поля измерен у неск. сотен звёзд различных
спектральных классов. Выяснено, что
индукция магн. поля на поверхности т.н. магнитных
звёзд
достигает неск. тысяч Гс, а у звезды HD 215441 наблюдается сильное поле ![]() Гс. Очень сильные магн. поля, превосходящие 10
Гс, обнаружены по 3. э. у нескольких вырожденных звёзд - белых карликов.
Гс. Очень сильные магн. поля, превосходящие 10
Гс, обнаружены по 3. э. у нескольких вырожденных звёзд - белых карликов.
Магн. поля Галактики можно измерить по зеемановскому расщеплению радиолинии водорода 21 см. Выбор линии поглощения для таких
измерений позволяет наблюдать на фоне яркого радиоисточника резкую линию и значительно
уменьшить роль шумов и возможных ошибок. Таким методом были измерены магн. поля в
плотных
и холодных облаках межзвёздного газа, проецирующихся на яркие галактич. радиоисточники:
Кассиопея А, Телец А и др. Оказалось, что в облаке, расположенном в направлении источника
Кассиопея А, магн. поле достигает ![]() Гс. Среднее
крупномасштабное поле Галактики имеет величину
Гс. Среднее
крупномасштабное поле Галактики имеет величину ![]() Гс, а
в облаках газа магн. поле в 5-10 раз больше. Таким путём определяется только продольный
(вдоль луча зрения) компонент магн. поля.
Гс, а
в облаках газа магн. поле в 5-10 раз больше. Таким путём определяется только продольный
(вдоль луча зрения) компонент магн. поля.
Изучение магн. полей активных областей, пятен и др. образований на Солнце производится
с помощью особых чувствительных приборов - фотоэлектрич. магнитографов, позволяющих
измерять поля до 1 Гс и меньше (составляющую поля по лучу зрения). При таких измерениях
также используется обратный 3. э. В большинстве случаев зеемановские компоненты линии
сливаются между собой - наличие магн. поля вызывает общее расширение спектр. линии.
Магн. поле определяется в этих случаях поляризац. методами. При наблюдениях аномального
3. э., когда линия расщепляется на ряд ![]() - и
- и ![]() -компонентов,
для определения величины расщепления (
-компонентов,
для определения величины расщепления (![]() )
) ![]() -компонентов
астрофизики используют ф-лу:
-компонентов
астрофизики используют ф-лу: ![]() , где Н выражено в Э, длина волны
, где Н выражено в Э, длина волны ![]() в
в ![]() .
Обычно для измерений солнечных магн. полей используют спектр. линию железа
.
Обычно для измерений солнечных магн. полей используют спектр. линию железа ![]() (FeI) с фактором g= 3 и ряд др. линий. Поскольку зеемановские
компоненты линии поляризованы различно (в продольном 3. э. линии имеют правую и левую
круговую поляризацию, в общем случае - эллиптическую), изменение знака наблюдаемой
поляризации
смещает линию. Величина смещения, фиксируемая фотоэлектрич. магнитографом, определяет
продольную составляющую напряженности поля. Для получения информации о величине и
направлении
полного вектора магн. поля на Солнце необходимо измерить параметры поляризации в
нек-ром участке спектр. линии и использовать результаты теории образования линий
в магн. поле.
Для этой цели обычно принимается нек-рая модель атмосферы и предполагается однородность
магн. поля в слое образования спектр. линии. Полный вектор индукции магн. поля измеряется
с гораздо меньшей точностью (50-100 Гс). Общее магн. поле Солнца как звезды составляет
в среднем ок. 1 Гс, однако в солнечных пятнах величина поля значительно выше и достигает
неск. тысяч Гс.
(FeI) с фактором g= 3 и ряд др. линий. Поскольку зеемановские
компоненты линии поляризованы различно (в продольном 3. э. линии имеют правую и левую
круговую поляризацию, в общем случае - эллиптическую), изменение знака наблюдаемой
поляризации
смещает линию. Величина смещения, фиксируемая фотоэлектрич. магнитографом, определяет
продольную составляющую напряженности поля. Для получения информации о величине и
направлении
полного вектора магн. поля на Солнце необходимо измерить параметры поляризации в
нек-ром участке спектр. линии и использовать результаты теории образования линий
в магн. поле.
Для этой цели обычно принимается нек-рая модель атмосферы и предполагается однородность
магн. поля в слое образования спектр. линии. Полный вектор индукции магн. поля измеряется
с гораздо меньшей точностью (50-100 Гс). Общее магн. поле Солнца как звезды составляет
в среднем ок. 1 Гс, однако в солнечных пятнах величина поля значительно выше и достигает
неск. тысяч Гс.
Особый интерес представляют сверхсильные магн. поля ~ 106-109
Гс у поверхности нек-рых белых карликов и ~ 1011-1013
Гс (а может быть, и выше) у поверхности ряда нейтронных
звёзд. В сверхсильных полях разрушается связь орбитальных и спиновых моментов
(li и si),
к-рые в отсутствие поля образуют моменты L и S: L=![]() , S=
, S=![]() . В результате
имеет место 3. э. отдельных квазинезависимых электронов. В очень сильных полях нарушается
центральная симметрия атома, и атом (или ион) приобритает форму веретена. Такая ситуация
имеет место на поверхности нейтронных звёзд
. В результате
имеет место 3. э. отдельных квазинезависимых электронов. В очень сильных полях нарушается
центральная симметрия атома, и атом (или ион) приобритает форму веретена. Такая ситуация
имеет место на поверхности нейтронных звёзд
(Л.А. Вайнштейн, В.М. Томозов)
Л. А. Вайнштейн, В. М. Томозов, "Физика Космоса", 1986
Глоссарий Astronet.ru
|
Публикации с ключевыми словами:
эффект Зеемана - магнитное поле - спектральные линии - расщепление спектральных линий
Публикации со словами: эффект Зеемана - магнитное поле - спектральные линии - расщепление спектральных линий |

|
См. также:
Все публикации на ту же тему >> | |