Астронет > Плазменная турбулентность

по текстам по ключевым словам в глоссарии по сайтам перевод по каталогу

На сайте

Астрометрия

Астрономические инструменты

Астрономическое образование

Астрофизика

История астрономии

Космонавтика, исследование космоса

Любительская астрономия

Планеты и Солнечная система

Солнце

Плазменная турбулентность

1. Введение
2. Квазилинейная теория
3. Индуцированное рассеяние волн
4. Взаимодействие волна-волна
5. Сильная ленгмюровская турбулентность

1. Введение

П. т.- состояние плазмы (П), в к-ром возбуждены интенсивные колебания, имеющие нерегулярный, шумовой характер. По мере развития физики космич. П. всё более ясным становится тот факт, что учёт специфич. св-в П. т., т. е. турбулентности разреженной среды с редкими столкновениями и доминирующим коллективным взаимодействием, важен для правильного решения многих астрофизич. проблем. В качестве примера можно привести физику магнитосфер планет и такие её ключевые задачи, как захват и динамика заряженных частиц в радиац. поясах, механизмы аномально быстрой диссипации энергии солнечного ветра на фронте ударной волны магнитосферы, проблемы пересоединения силовых линии магн. поля и др. Без привлечения представлений П. т., по-видимому, невозможно объяснить, например, радиоизлучение Солнца, планет, высокочастотное излучение пульсаров.

Во всех перечисленных случаях возникновение турбулентности связано с неустойчивостью (Н) исходного состояния космич. П. Вследствие Н амплитуды колебаний П нарастают до нелинейного уровня, при к-ром становятся существенными сложные процессы взаимодействия и взаимной трансформации колебаний. Здесь имеется определённая аналогия с гидродинамич. турбулентностью. Как известно, при больших скоростях потока, т.е. при больших числах Рейнольдса, течение становится неустойчивым и разбивается на отдельные крупномасштабные вихри. Взаимодействие между вихрями приводит к непрерывному дроблению их масштабов (т.е. возникновению всё более мелких вихрей), происходящему вплоть до подключения малых масштабов, для к-рых существенно затухание, обусловленное вязкостью. Дробление масштабов вихрей соответствует перекачке энергии турбулентных движений из длинноволновой в коротковолновую область спектра. Др. пример такой перекачки энергии в гидродинамич. турбулентности - это укручение (увеличение крутизны) и опрокидывание волнового фронта звуковых волн в жидкости и газе.

Между плазменной и гидродинамич. турбулентностями имеются два существенных различия. Первое связано со специфич. св-вами П, в к-рой для большинства видов волн существует дисперсия фазовой скорости, т.е. зависимость фазовой скорости от длины волны (см. Дисперсия волн). Расплывание волновых пакетов, обусловленное дисперсией, способно ограничивать эффект укручения (подробнее см. в ст. Бесстолкновительные ударные волны). Вследствие этого непрерывно дробящиеся вихри в П. т. не образуются, а произвольные движения П всегда можно представить как суперпозицию взаимодействующих между собой установившихся волн.

Второе различие связано с тем, что в П важную, а иногда и определяющую роль играет резонансное взаимодействие колебаний и волн с частицами, обусловленное индуцированными (т.е. происходящими "с помощью" уже имеющихся в данной спектр, области колебаний и волн) излучением, поглощением и рассеянием волн частицами (см. ниже). В равновесной П такое взаимодействие приводит к бесстолкновительной диссипации волн (см. Ландау затухание). В неравновесной П могут преобладать процессы индуциров. излучения волн, приводящие к развитию многочисл. Н. Обратное воздействие возникших при Н колебаний и волн на функцию распределения неустойчивого состояния, стремясь устранить или, по крайней мере, ограничить фактор, вызывающий Н, приводит к бесстолкновителыюй релаксации неустойчивого распределения (аномально быстрое торможение электронного пучка в П, аномально большое сопротивление протеканию электрич. тока, аномальные теплопроводность, вязкость и др.).

В П спектр возможных колебаний и волн (ленгмюровские, ионно-звуковые, альвеновские и др., см. Плазма) несравненно богаче, чем в жидкости. Соответственно можно говорить о различных типах П. т. (ленгмюровской, ионно-звуковой и др.). Возможна также смешанная турбулентность, в к-рой присутствует неск. типов взаимодействующих волн. По этой причине П. т. значительно сложнее гидродинамич. турбулентности.

Обычный путь в изучении турбулентных процессов в П состоит прежде всего в исследовании различных Н (рассмотрены в ст. Неустойчивости плазмы), приводящих к возбуждению интенсивных колебаний П, затем исследуются возможные механизмы нелинейного ограничения Н и одновременного развития из них турбулентных процессов в П.

Такой путь чрезвычайно сложен и до настоящего времени полностью реализован только для т.н. слабой турбулентности П, теорию к-рой можно считать завершённой. Хотя ур-ния, описывающие колебания и волны в П, существенно нелинейны, при малых амплитудах (малых отклонениях от равновесия) в этих ур-ниях можно пренебречь членами, содержащими второй и более высокие порядки амплитуды (чем выше порядок, тем меньше величина эффекта, описываемого данным членом). Для получающихся в таком приближении волн и колебаний П справедлив принцип суперпозиции, т.е. отсутствует взаимодействие между волнами. Соответствующая теория волн и колебаний в П получила название линейной теории. В теории слабой турбулентности амплитуды волн также считаются малыми - энергия волновых движений существенно меньше тепловой энергии частиц. Поэтому здесь используются те же волны и колебания, что и в линейной теории, а произвольные волновые движения П представляются в виде разложения по таким волнам. Однако в ур-ниях для колебаний и волн в П в этом случае сохраняются малые нелинейные члены, описывающие взаимодействие волн, а также взаимодействие между волнами и частицами. За счёт такого взаимодействия амплитуды разложений, т.е. амплитуды отдельных волн, медленно (по сравнению с периодом колебаний) изменяются со временем.

2. Квазилинейная теория

В теории слабой турбулентности взаимодействие волн и частиц обычно описывается в рамках квазилинейного приближения. В таком приближении колебания и волны в П рассматриваются как линейные (пренебрегается взаимодействием между волнами), а единственным учитываемым нелинейным эффектом явл. изменение функции распределения резонансных частиц (т.е. частиц, скорости к-рых удовлетворяют условию соответствующего резонанса) в результате индуциров. излучения и поглощения волн этими частицами.

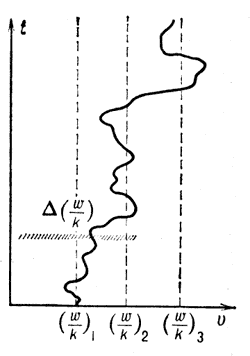
Рис. 1. Траектория частицы в пространстве
скоростей при наличии резонанса с тремя
волнами. $\Delta(\omega/k)\approx\sqrt{e\varphi_0/m}$ - ширина отдельного
резонанса волна-частица. Резонансы для соседних
волн перекрываются. t - время, v - скорость.

Простейший резонанс между волнами и частицами - черенковский, когда проекции скорости частиц на направление распространения волны v_x, близки к v_ф - фазовой скорости волны: $v_x\approx v_{ф}=\omega/k$ . В случае такого резонанса осн. нелинейный механизм при взаимодействии частиц с отдельной (монохроматической) волной - захват резонансных частиц в потенциальную яму, созданную волной, и их колебания в этой яме. Соответственно ширина черенковского резонанса порядка скорости колебаний захваченных частиц: $|v_x-\omega_k/k|\le\sqrt{q\varphi_0/m}$ , где $\varphi_0$ - амплитуда электрич. потенциала в волне, q и m - заряд и масса частицы. При наличии 2-3 волн точная задача о движении резонансных частиц становится чрезвычайно сложной. В квазилинейной теории, однако, используется приближённый статистич. подход, основанный на предположении о том, что в неустойчивой П возбуждается много волн со случайными фазами и близкими значениями фазовой скорости, так что области резонанса для соседних волн перекрываются. При этом происходит своего рода "коллективизация" резонансных частиц между соседними волнами. В результате случайных толчков со стороны многих волн происходит диффузия частиц по скорости (т.е. расплывание области, занятой частицами в пространстве скоростей). Траектории частиц в пространстве скоростей представляют собой броуновское блуждание, наложенное на свободное движение частиц (рис. 1). С течением времени траектории достаточно плотно заполняют весь интервал скоростей частиц, резонансных с присутствующими в П волнами $(\omega/k)_{мин} < v < (\omega/k)_{макс}$ - в результате диффузии функция распределения будет выравниваться, т.е. на ней появится "плато" во всём указанном интервале скоростей. Такой процесс в физике П обычно наз. квазилинейной релаксацией неустойчивой функции распределения.

В качестве примера рассмотрим квазилинейную релаксацию электронного пучка в П. В этом случае верхняя граница "плато" близка к начальной скорости пучка u₀, в то время как нижняя граница сравнима с тепловой скоростью электронов П v_Te (рис. 2). Достаточно быстрый ( $u_0\gg v_{T_e}$ ) электронный пучок в результате квазилинейной релаксации теряет (за время $\approx$ 5-10 обратных инкрементов пучковой Н) на возбуждение колебаний 2/3 своей первоначальной энергии.

Несколько сложнее процесс квазилинейной релаксации при циклотронной Н. Эта Н возникает в П, помещённой в магн. поле, когда ф-ция распределения по скоростям анизотропна, т.е. ср. энергия вдоль магн. поля отлична от ср. энергии поперёк поля. Н такого распределения обусловлена циклотронным индуциров. излучением эл.-магн. волн резонансными частицами. Возбуждаются свистящие атмосферики (свисты), если резонансные частицы - электроны, и альвеновские волны в случае резонанса с протонами. Условие циклотронного резонанса: $\omega-k_{||}/v_{||}=\omega_H$ . Поскольку частота излучаемой волны $\omega$ меньше циклотронной частоты $\omega_H$ , то скорости резонансных частиц вдоль магн. поля v_|| отрицательны, т.е. резонансные частицы движутся в сторону, обратную направлению распространения волны (k_|| - компонент волнового вектора, параллельный магн. полю).

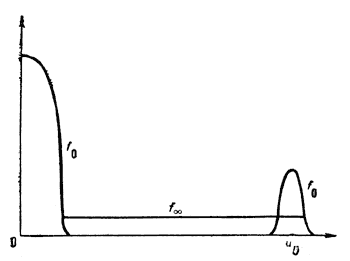
Рис. 2. Квазилинейная релаксация электронного
пучка в плазме. f₀ - начальная, неустойчивая функция
распределения (максимум при v= 0 соответствует
равновесной плазме, максимум при v=u₀ - пучку), $f_\infty$ -
функция распределения с "плато".

Так же как и в случае черенковского резонанса, циклотронное излучение волн сопровождается диффузией резонансных частиц в пространстве скоростей. Однако, в отличие от черенковского резонанса, эта диффузия явл. двухмерной - электрич. поле эл.-магн. волны E вызывает поперечную диффузию (т.е. изменяется перпендикулярный магн. полю компонент скорости $v_\perp$ ), а за счёт силы Лоренца $e[{\bf v}_\perp{\bf H}]/c$ , связанной с магн. полем волны, происходит диффузия частиц по продольной скорости. Поскольку электрич. поле эл.-магн. волны вихревого происхождения и в системе отсчёта волны оно обращается в нуль, то в этой системе отсчёта энергия частиц должна сохраняться. Соответственно линии диффузии представляют собой окружности, центры к-рых смещены по v_|| вправо на величину фазовой скорости волны $v_\perp^2+(v_{||}-\omega/k)^2$ =const (рис. 3). В результате квазилинейной диффузии эти линии в пространстве скоростей становятся линиями уровня, вдоль к-рых образуется "плато" на ф-ции распределения. Квазилинейная релаксация анизотропных распределений частиц в магн. ловушках, напр. в магнитосфере, приводит к диффузионному потоку резонансных частиц из области удержания в конус потерь (см. Магнитосферы планет). Для магнитосферы Земли это осн. механизм, определяющий время жизни энергичных частиц в радиац. поясах. Изотропизация распределения резонансных частиц - осн. следствие циклотронной Н. Энергия эл.-магн. колебаний, возбуждаемых при циклотронной Н, составляет обычно небольшую долю ( $\sim\omega/\omega_H$ ) энергии резонансных частиц.

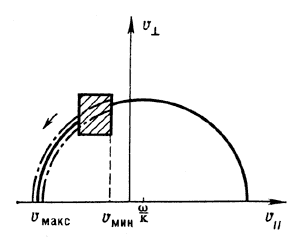
Рис. 3. Диффузия частиц в пространстве
скоростей в случае циклотронного резонанса
с волнами. Заштрихована область, в
которой первоначально находятся резонансные
частицы, стрелка показывает направление
диффузии. Диффузия сопровождается
изотропизацией распределения резонансных
частиц по скоростям (штрихпунктир) и
потерей ими части энергии, переходящей
в колебания. $v_{||}, v_\perp$ - параллельная
и перпендикулярная магнитному полю
составляющие скорости.

Ещё одна важная для космич. физики Н - т.н. шланговая. Она также развивается в анизотропной П. Для её появления продольная темп-ра и давление П должны существенно превышать поперечные. За счёт шланговой Н магн. силовые линии извиваются беспорядочным образом, так что магн. поле турбулизуется. Обратное влияние этой турбулентности на неустойчивую П можно понять, если воспользоваться условиями сохранения адиабатич. инвариантов: $mv_\perp^2/H={\rm const},\; \int v_{||}\;dl={\rm const}$ (интеграл вычисляется вдоль силовой линии магн. поля между точками отражения частиц, dl - длина элемента силовой линии). Ясно, что по мере роста турбулентного магн. поля растут поперечные скорости частиц $v_\perp$ (а следовательно, и поперечные давления) и уменьшаются продольные скорости и давление (поскольку при запутывании силовых линий увеличивается длина l). Давление изотропизуется, т.е. и в этом случае под действием П. т. происходит бесстолкновительная релаксация анизотропной П.

3. Индуцированное рассеяние волн

Квазилинейная теория описывает только процессы индуциров. излучения и поглощения волн резонансными частицами. Из большого числа, вообще говоря, более слабых нелинейных эффектов, возникающих в высших порядках по амплитуде колебаний, в теории П. т. особо важная роль принадлежит эффекту резонансного взаимодействия частиц с биениями разностной частоты между двумя любыми колебаниями, возбужденными в турбулентной П. Поскольку эти биения можно рассматривать, в определённом смысле, как новые волны, то условие черенковского резонанса частиц с ними записывается в виде: $({\bf k-k_1)v}=\omega_k-\omega_{k_1}$ k, $$(\omega_k что может оказаться меньше тепловой скорости частиц. В этом случае в резонанс с биениями вовлекается осн. масса тепловых частиц П, в то время как условие черенковского резонанса при индуциров. излучении и поглощении волн выполняется только для небольшой группы надтепловых частиц (пучка). Поэтому хотя резонанс на биениях нелинейный, т.е. возникает в высших порядках по амплитуде волн, из-за большего числа рассеивающих частиц он может оказаться весьма существенным в динамике спектра волн. При рассеянии на тепловых частицах П частота рассеянного кванта всегда меньше частоты исходного, поскольку часть энергии передаётся рассеивающей частице (нелинейное затухание Ландау). Для ленгмюровских волн, как, впрочем, и для др. волн с норм. дисперсией (<img src=$ k), такое уменьшение частоты при рассеянии означает уменьшение волнового числа. Т.о., при индуциров. рассеянии ленгмюровских волн спектр, перекачка энергии происходит в сторону больших длин волн, т.е. больших фазовых скоростей (в отличие от привычной картины - гидродинамич. турбулентности, когда перекачка энергии происходит от больших масштабов к меньшим). width="149" height="18" >. Если волны в турбулентной П рассматривать height="16" > и импульсом $\hbar {\bf k}$ , то условие резонансного 005/01/15/0001201969/tex/formula20.gif" border="0" alt="$\omega_k$" align="absmiddle" width="16" height="12" >) border="0" alt="$\omega_{k_1}$" align="absmiddle" width="21" height="12" >). -\omega_{k_1})(k-k_1)$" align="absmiddle" width="128" height="18" > настолько мала, 9/tex/formula8.gif" border="0" alt="$\omega$" align="absmiddle" width="10" height="9" > растёт

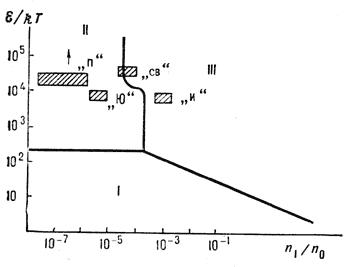
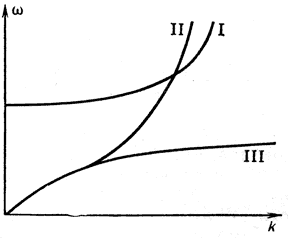
Рис. 4. Границы действия различных механизмов
релаксации электронных пучков в плазме: I -
квазилинейная теория, II - область
индуцированного рассеяния, III - область, где
существенны эффекты сильной турбулентности.
Отмечены также параметры различных
космических явлений, для которых существенны
коллективные механизмы релаксации пучков в
плазме: "и" - потоки быстрых частиц,
проникающих в авроральных областях в
ионосферу, "св" - электронные пучки,
возникающие при хромосферных вспышках в
плазме солнечного ветра, "п" - электронные
пучки в магнитосферах пульсаров, "Ю" - пучки,
взаимодействующие с плазмой солнечного ветра
в районе магнитопаузы Юпитера.

Одно из важных следствий эффекта индуциров. рассеяния волн - нелинейная стабилизация пучковой Н. В основе пучковой Н лежит эффект индуциров. излучения волн пучком, когда возбуждению волн с определённой частотой и длиной волны "помогают" уже имеющиеся в этой спектральной области волны. Если скорость спектр. перекачки, обусловленной индуциров. рассеянием, достаточно велика, то волны, увеличивая свою фазовую скорость, покидают резонансную с пучком область спектра, прежде чем успевают эффективно с ним провзаимодействовать. В результате должна происходить стабилизация пучковой Н. Реально, однако, энергия резонансных с пучком колебаний возрастает до уровня, при к-ром скорости обоих процессов (скорость роста колебаний из-за Н и скорость спектр. перекачки) сравниваются. Поскольку энергия резонансных колебаний при этом может оказаться существенно меньше энергии пучка, частицы пучка будут крайне медленно рассеиваться такими колебаниями, и П становится как бы прозрачной для электронного пучка. На рис. 4 приведены для плоскости параметров n₁/n₀, $\varepsilon/kT$ (n₁, n₀ - соответственно плотности пучка и П, $\varepsilon$ - энергия частиц пучка, Т - темп-ра П) области действия различных механизмов релаксации пучка в П. Граница между областью применимости квазилинейной теории и областью, где существенна нелинейная стабилизация пучковой Н из-за индуциров. рассеяния, определяется соотношением: $\varepsilon/kT\approx[30 u_0 M/\Delta um_e]^{1/3}$ , где М - масса иона, $\Delta u$ - разброс по скоростям в пучке. Из рис. 4 видно, что во многих случаях (релятивистские электронные пучки в магнитосферах пульсаров, электронные пучки, взаимодействующие с П солнечного ветра в районе ударной волны юпитерианской магнитосферы) доминирует индуциров. рассеяние, т.е. существен эффект "нелинейного просветления" П для электронов пучка.

4. Взаимодействие волна-волна

Рис. 5. Распадные (II) и нераспадные (I, III)
спектры волн в плазме.

До сих пор мы рассматривали эффекты в турбулентной П, основанные на взаимодействии волна-частица. Однако если амплитуды волн не слишком малы, в динамике турбулентности могут стать существенными эффекты нелинейного взаимодействия между волнами. Если использовать аналогию турбулентной П со смесью двух газов - газа частиц (электронов, ионов) и газа квазичастиц (элементарных волновых возбуждений), то эти новые нелинейные эффекты можно интерпретировать как взаимодействия внутри газа квазичастиц. Простейшие взаимодействия такого типа - распады и слияния в системе трёх волн. При этом должны выполняться распадные условия для частот и волновых векторов взаимодействующих волн: $\omega_k=\omega_{k_1}+\omega_{k_2}$ , k = k₁+k₂, являющиеся следствием законов сохранения энергии и импульса волновых квантов [приведённые распадные условия записаны для распада кванта (k, $\omega_k$ ) на кванты (k₁, $\omega_{k_1}$ ), (k₂, $\omega_{k_2}$ )]. Далеко не всякий спектр плазменных колебаний явл. распадным, т.е. не при каждой дисперсионной зависимости ( $\omega({\bf k})$ ) могут быть выполнены распадные условия. На рис. 5 приведены примеры распадных (II) и нераспадных (I, III) спектров. Поскольку плазменные колебания имеют множество различных ветвей (ветвей дисперсионной кривой), то распадные условия могут выполняться для колебаний, принадлежащих различным ветвям, если только через три точки на этих ветвях можно провести кривую, аналогичную II. Напр., для ленгмюровской волны (спектр нераспадный) распадные условия выполняются при распаде на ленгмюровскую и ионно-звуковую волны. Возможны и др. варианты конверсии (взаимного превращения) различных типов волн в П, напр. рождение ленгмюровских и ионно-звуковых волн при распаде эл.-магн. волны. В тех случаях, когда распадные условия для трёх волн не выполняются, в элементарный акт взаимодействия включаются сразу четыре волны и соответственно этому взаимодействие между волнами в слабой турбулентности становится более медленным (при трёхволновых взаимодействиях обратное время эволюции спектр. плотности числа волновых квантов N_k пропорционально первой степени этой плотности, в то время как при четырёхволновых взаимодействиях это время пропорционально квадрату плотности).

Эволюция спектров волн, обусловленная нелинейным взаимодействием, описывается кинетич. ур-нием для величин N_k. Это ур-ние кроме очевидного равновесного решения: распределения Рэлея-Джинса $N_k={\rm const}/\omega_k$ - имеет также стационарные решения с переносом энергии по спектру, т.е. в пространстве волновых чисел. Эти решения соответствуют такой ситуации, когда приток энергии в турбулентные движения происходит в области больших масштабов, нелинейное взаимодействие создаёт поток энергии к меньшим масштабам, для к-рых существенна диссипация. Здесь имеется полная аналогия с гидродинамич. турбулентностью. Между крупными масштабами области притока энергии и мелкими масштабами области затухания колебаний находится т.н. инерционный интервал, в к-ром спектр для многих типов турбулентности имеет универсальную форму, соответствующую постоянству потока энергии по спектру. В качестве примера такой турбулентности можно привести ионно-звуковую турбулентность. Процесс коротковолновой перекачки энергии в этом случае связан со слиянием ионно-звуковых квантов с почти коллинеарными волновыми векторами. Коллинеарность необходима для выполнения распадных условий, поскольку спектр длинноволновых ионно-звуковых колебаний близок к линейному. Из условия постоянства потока энергии по спектру следует, что для каждого масштаба турбулентности r, имеющего характерные скорости колебаний частиц v, выполнено соотношение v⁴r= const, что соответствует спектр. плотности ионно-звуковых квантов: N_k= const /k^3/2.

5. Сильная ленгмюровская турбулентность

Значительно сложнее решается задача о турбулентности ленгмюровских колебаний и волн. Дело в том, что спектр ленгмюровских волн - нераспадный и основные нелинейные взаимодействия для ленгмюровских волн в слабой турбулентности связаны с уже описанным выше процессом индуциров. рассеяния волн на частицах П либо с распадом ленгмюровской волны на ленгмюровскую и ионно-звуковую. При каждом из этих процессов должно происходить "покраснение" (увеличение длины волны) ленгмюровского кванта (плазмона), поскольку часть энергии плазмона передаётся либо рассеивающей частице, либо ионно-звуковому кванту. Т.о., нелинейное взаимодействие в ленгмюровской турбулентности создаёт поток энергии в длинноволновую область, где вообще отсутствуют механизмы поглощения ленгмюровских колебаний. В результате возникает парадокс образования плазменного конденсата: если в П имеется источник ленгмюровских колебаний (пучок, эл.-магн. волна), то в конечном счёте энергия этого источника будет накапливаться в виде очень длинноволновых ( $k\to 0$ ) ленгмюровских волн, не поглощающихся в П и будет неограниченно нарастать со временем, что в принципе невозможно. Решение этого парадокса невозможно в рамках слабой турбулентности, оно основано (см. ниже) на использовании модуляц. Н ленгмюровских волн. Это Н плазменного конденсата, т.е. достаточно интенсивного газа длинноволновых плазмонов, относительно процесса модуляции его плотности. Н приводит к образованию каверн - областей повышенной концентрации плазмонов, из к-рых под действием силы высокочастотного давления, создаваемого плазмонами (аналог давления излучения), вытеснена П. Характерный размер каверн, образующихся в результате модуляц. Н, $L\sim k^{-1}\sim D\sqrt{n_0/|\delta n|}$ обычно порядка 10-30 дебаевских радиусов D ( $\delta n$ - вариации плотности П в кавернах). В лабораторной П из-за малой величины D наблюдение таких структур крайне затруднено. Осн. наблюдения модуляц. Н ленгмюровских волн относятся к космич. условиям (разреженная П, большие D). На рис. 6 показана пространств. структура интенсивных ленгмюровских волн, возбуждаемых в П солнечного ветра в районе ударной волны юпитерианской магнитосферы, где $D\approx$ 20 м, что позволяет относительно легко разрешить ("увидеть") микроструктуру отдельных каверн. В процессе развития модуляц. Н плазмоны оказываются запертыми в кавернах, подобно тому как заряженные частицы запираются в достаточно глубоких электрич. потенциальных ямах. Этот нелинейный эффект уже не может быть описан в рамках слабой турбулентности, т.е. в рамках слабого взаимодействия колебаний и волн линейной теории. Поэтому принято считать, что модуляц. Н приводит к сильной ленгмюровской турбулентности.

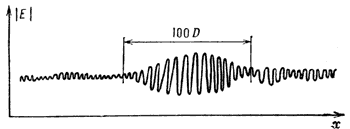
Рис. 6. Ленгмюровская каверна в космической плазме
по данным наблюдений в районе магнитопаузы Юпитера.
|E| - модуль напряжённости электрического поля.

В теории сильной ленгмюровской турбулентности важное значение имеет явление коллапса ленгмюровских волн, т.е. самопроизвольного схлопывания каверн с запертыми в них плазмонами. Это схлопывание носит характер "взрыва", т.е. происходит с нарастающей скоростью вплоть до того момента, когда каверна достигает столь малых размеров, что длина волны запертых в ней плазмонов сравнивается с D, а фазовая скорость соответственно - с тепловой скоростью. При этом включается затухание Ландау ленгмюровских колебаний, и диссипация их энергии останавливает коллапс.

Теория сильной ленгмюровской турбулентности, базирующаяся на явлении коллапса, оказывается в значит. степени аналогичной теории гидродинамич. турбулентности. Источник турбулентности находится в области больших масштабов. Коротковолновая перекачка ленгмюровских колебаний осуществляется за счёт схлопывания каверн с запертыми в них плазмонами, в области малых масштабов происходит бесстолкновительное поглощение плазмонов. С этим и связано решение возникающего в теории слабой турбулентности парадокса плазменного конденсата. Спектр. плотность плазмонов в инерционном интервале можно найти, используя законы схлопывания каверн: N_k= const /k^5/2

В том случае, когда ленгмюровские колебания возбуждаются при взаимодействии с П электронного пучка, коротковолновая спектр. перекачка колебаний, обусловленная модуляц. Н и коллапсом, может приводить к стабилизации пучковой Н. Этот механизм стабилизации пучковой Н существен для пучков высоких энергий и относительно большой плотности (рис. 4): потоки быстрых электронов, образующиеся в П солнечного ветра при вспышках на Солнце, электроны с высокой энергией, вторгающиеся в ионосферу в авроральных областях, и др. Граница между областью III, где существенны эффекты сильной турбулентности, и областью I, где применима квазилинейная теория релаксации, определяется соотношением $n_1/n_0=10(kT/\varepsilon)^3 u_0/\Delta u$ . Граница между областью III и областью II, в к-рой существенно индуциров. рассеяние ленгмюровских колебаний частицами П, определяется соотношением $n_1/n_0\approx m/3M$ в том случае, когда релаксируют пучки не слишком большой энергии $(\varepsilon/kT\ll 3M/m)$ , и $n_1/n_0\approx(\Delta u/u)^2 m/3M$ в обратном случае $(\varepsilon/kT\gg 3M/m)$ .

Скорость спектр. перекачки ленгмюровских колебаний и их последующей диссипации в сильной турбулентности обычно столь велика, что плотность энергии возбуждаемых пучком колебаний W "заморожена" па пороге модуляц. Н: $W\approx 3k_0^2 D^2 n_0 kT, k_0\simeq\omega_{0e}/u_0$ - волновое число резонансных с пучком колебаний. Превышение этого порога приводит к тому, что процесс возбуждения колебаний уже не может конкурировать с их диссипацией и колебания вновь возвращаются на порог. Относительно низкий уровень резонансных с пучком ленгмюровских колебаний приводит к существенному затягиванию процесса коллективной релаксации пучка в П. Этот эффект имеет место, напр., для образующихся при вспышках на Солнце электронных пучков, взаимодействующих с П солнечного ветра (рис. 7). Трансформация ленгмюровских колебаний, возбуждаемых такими пучками, в эл.-магп. излучение приводит к солнечным радиовсплескам III типа (см. Радиоизлучение Солнца).

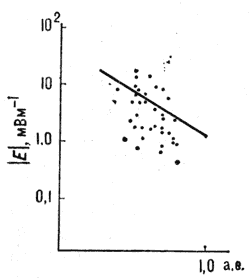
Рис. 7. Пространственное распределение
энергии плазменных колебаний по данным
наблюдений в плазме солнечного ветра.
Сплошная линия - теоретическая оценка по
порогу модуляционной неустойчивости. |E| -
модуль напряжённости электрического поля, по
горизонтальной оси - расстояние от Солнца.

Вообще, для многих задач астрофизики (напр., радиоизлучение Солнца, планет) весьма важны механизмы трансформации ленгмюровских колебаний в эл.-магн. волны. Наряду со всплесками III типа эффекты трансформации наиболее существенны в солнечных радиовсплесках II типа (превращение в эл.-магн. волны плазменных волн, генерируемых на фронте ударной волны, oбразованной вспышкой на Солнце), в километровом излучении Земли (радиоизлучение ленгмюровской турбулентности, создаваемой быстрыми потоками электронов в магнитосфере) и во многих др. подобных эффектах.

Выше было показано, что распад ленгмюровских колебаний может идти только с уменьшением частоты, т.е. не может непосредственно приводить к трансформации в эл.-магн. волны. Вместе с тем неизбежным спутником сильной ленгмюровской турбулентности явл. интенсивные квазинейтральные флуктуации плотности П. Конверсия ленгмюровских колебаний на этих флуктуациях плотности должна приводить к их трансформации в эл.-магн. волны. Этот механизм, по-видимому, явл. основным в радиовсплесках III типа. Вместе с тем существенным может оказаться и др. механизм трансформации в эл.-магн. волны - слияние двух ленгмюровских квантов с образованием эл.-магн. кванта на удвоенной ленгмюровской частоте. Поэтому при солнечных всплесках II и III типов излучение появляется сразу на двух гармониках, частоты к-рых относятся как 2:1.

Лит.:
Арцимович Л.Л., Сагдеев Р.3., Физика плазмы для физиков, М., 1979; Кадомцев Б. В., Коллективяые явления в плазме, М., 1976; Веденов А.А., Рютов Д. Д., Квазилинейные эффекты в потоковых неустойчивостях, в сб.: Вопросы теории плазмы, в. 6, М., 1972; Галеев А.А., Сагдеев Р.3., Нелинейная теория плазмы, там же, в. 7, М., 1973; Пикельнер С.Б., Основы космической электродинамики, 2 изд., М., 1966; Цытович В.Н., Нелинейные эффекты в плазме, М., 1967; Gurnett D.A., Anderson R. В., "Science", v. 194, р. 1159.

(В.Д. Шапиро)

В. Д. Шапиро, "Физика Космоса", 1986
Глоссарий Astronet.ru

А | Б | В | Г | Д | З | И | К | Л | М | Н | О | П | Р | С | Т | У | Ф | Х | Ц | Ч | Ш | Э | Я

Публикации с ключевыми словами: плазменная турбулентность - Плазма - турбулентность
Публикации со словами: плазменная турбулентность - Плазма - турбулентность

Карта смысловых связей для термина ПЛАЗМЕННАЯ ТУРБУЛЕНТНОСТЬ

См. также:

Один год на Солнце

"Z-машина" устанавливает неожиданный рекорд температуры на Земле

Альвеновские волны в коллапсирующих протозвездных облаках

От плазмы солнечной короны к плазме на нейтронных звездах

Плазма

Танец Солнца

Турбулентная область вокруг звезды Эта Киля

Все публикации на ту же тему >>

Обсудить эту публикацию

Версия для печати