III. THE LIN-SHU THEORY
| I would like to acknowledge that Professors Lin and Toomre of MIT are also interested in the problem of spiral structure, and that I have benefited from discussions with them as well as their students. |
| Kalnajs 1963, p.13 |
3.1 Working hypothesis and semi-empirical theory
| In hindsight, considering the crucial influence that the Lin & Shu (1964) paper had on the thinking of astronomers, it is only regretful that Lin did not decide (with or without me) to publish even earlier, because he certainly had all the physical ideas contained in our paper well before 1964. |
| Shu 2001 |
While Toomre, Hunter and Kalnajs had already presented their first results in the dynamics of flat galaxies, Lin still kept on thinking over the spiral problem. 63 Astronomers in Princeton had convinced him that, despite Chandrasekhar's criticism of Lindblad's theories, 64 the idea itself of a long-lived, shape-preserving spiral pattern is consistent with Hubble's classification system that relates spiral features with a galaxy's morphological type, its steady characteristic, thus suggesting that the spirals are steady as well. This view reminded Lin of wave modes in fluid flows that he had been studying for years back. 65 On purely heuristic grounds, discrete spiral modes seemed to him very reasonable as the natural result of wave evolution, and, if so, the patterns released might be associated with slowly growing or neutral modes. Lin raised this premise to the rank of working hypothesis, and around it as the nucleus he set to develop a semi-empirical theory. 66 It was seen to follow best the "urgent assignment from the astronomers [...] to make some specific calculations" and "to demonstrate the possibility of the existence of quasi-stationary spiral modes from the theoretical point of view [...] with understanding of the dynamical mechanisms relegated to a secondary and even tertiary position" (Lin). 67,68
"The conclusion in the working hypothesis is not proved or deuce, but supported by an accumulation of theoretical analysis and empirical data. The adoption of this working hypothesis is a very important step in the development of a theory of spiral structure. It means that the authors are committed to back it up with the comparison of subsequent predictions with observational data." (Lin)
The coauthor to share Lin's fame and commitment was his student Frank Shu (Shu 1964) 69 who "found it remarkable that a scientist trained as a professional mathematician would place higher priority on empirical facts than deductive reasoning" and believed that "it was this broad-mindedness and clear vision that gave Lin a considerable advantage over his many competitors of the period" (Shu). 70 The Lin and Shu paper "On the spiral structure of disk galaxies" (Lin & Shu 1964, hereinafter LS64), in which "they first demonstrated the plausibility of a purely gravitational theory for density waves by a continuum treatment" (Lin & Shu 1966, p.459), appeared in August 1964. 71
The paper considered small non-axisymmetric disturbances to a razor-thin cold disk and found for them, through the governing hydrodynamic and Poisson equations, wave-like solutions of the type
| (12) |
each specified by its eigenfunction (r) and a pair of eigenvalues and m. For further advancement, the WKBJ-method was applied. It is valid for the case of phase S(r) varying with radius much faster than amplitude A(r), which features the tightly wrapped spirals, ones of small pitch angle between the circumferential tangent and the tangent to the constant-phase line
| (13) |
Depending on the sign of a radial-wavenumber function k(r) = - S / r, the spirals are trailing (k > 0) or leading (k < 0) (Fig.8). With A(r) expanded in a series over a small parameter tani = m / kr (i being the pitch angle), the problem is solved to the lowest, i-independent order neglecting the azimuthal force component of spiral gravity. In this case, both leading and trailing arms act as just rings, so that the ensuing dispersion relation
| (14) |
substantially repeats Toomre's equation (5) for radial oscillations. Importantly, relation (14) is valid for Re{2} 1. This restricts the radial span of the WKBJ solutions, and in the neutral case Im{}= 0 they gain the territory between the Lindblad resonances determined by Eqn (11) and equating the angular speed of an m -armed spiral pattern to a combination
| (15) |
with the minus/plus sign discriminating, respectively, between the ILR and OLR. The two-armed spirals thus seem preferred as best covering an entire disk (Fig.9).
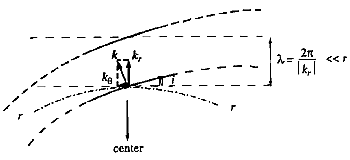 |
Figure 8. The WKBJ approximation and the tightly wrapped spiral waves. kr k and k << k are the components of the local wavenumber k. = 2 / k determines the radial interarm spacing; it is small compared to the galactocentric distance r since kr >> 1 (which is equivalent to small pitch angles i << 1). |
Such was the mathematical basis of the original Lin-Shu density-wave theory, called elementary by its authors any later (e.g. Bertin & Lin 1996, p.229). It treated wave quantities p, , and m as free parameters burdened with no dynamical imposition, which made the theory so comfortable in imitating spiral grand designs by means of the curves r() given by
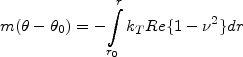 |
(16) |
and obtained through the integration of expressions (13) and (14). Sure, the results of this procedure were controvertible, already because the fast-growing waves - exactly those examined in LS64 - ruled out the proclaimed quasi-stationarity. 72 But the authors hoped that random motions, excluded from their analysis, would in fact stave off disk instability as definitively as to impose a state of near-stability open for slowly growing modes until a small but finite amplitude.
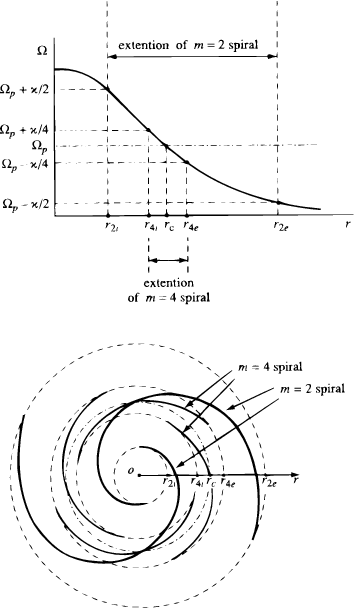 |
Figure 9. The Lindblad resonances as confining the region accessible for the tightly wrapped spiral waves. (a) - a rotation curve for a galaxy disk and its corresponding corotation and m = 2, 4 Lindblad resonances; (b) - the co-scaled view of the two and four armed tightly wrapped spirals. |
Toomre (1964) had reflected already on such a state of Q 1 as settling once all over the disk-like stellar Galaxy, but yet he found it stable still, at least in our solar region. As a counterpoise, Lin with Shu diagnosed instability for another region, at about r0 = 4 - 5 kpc from the center. With that, they pictured "a galactic disk, which is in part stable and in part unstable" and suggested "the possibility of a balance resulting in a neutral density wave extending over the whole disk and having a scale of the order of (but smaller than) the distance between the stable and unstable regions" (LS64, p. 651). It was this "suggestion of the possibility" that summarized Lin's early reflections and made his basic working hypothesis originally sound as a statement that
"the total stellar population, which has various degrees of velocity dispersion, forms a quasi-stationary spiral structure in space of the general nature discussed above" (LS64, p.651).
As we can see, this statement hinges almost entirely on the opinion that, for our galactic disk to be equally stable at that r0, the velocity dispersion must there exceed cr, min 80 ± 10 km/s, which cannot be the case, else "a considerable number of stars with high radial velocities would reach our neighborhood from the interior part of the Galaxy, contrary to observational evidence" (LS64, p.651). But was this opinion (the authors never repeated it) strong enough? First, it meant an inconceivable situation when some massive portion of a stellar galaxy remains unstable during all the period of formation in it of a global quasi-steady pattern. Secondly, and most important for astronomers, it had - already in 1964 - grave objections to the fact that the largest epicyclic deflection of the Lin-Shu "high radial velocity stars" from their `home' radius r0 = 4 - 5 kpc, equaled to r r0 cr / V0 21/2, was in frames of Schmidt's model (cited in LS64) 1 - 1.5 kpc only - too little to let those stars even come close from r0, if not reach us. We find that the original QSSS hypothesis of Lin and Shu, called nowadays "a preliminary formulation" only (Bertin & Lin 1996, p.80), rested on a rather weak basis, both dynamical and empirical.
Very interesting in LS64 is the authors' notice on what had made their work get to print so urgently. A passage following their opening discussion of "at least two possible types of spiral theories", one of which "is to associate every spiral arm with a given body of matter" and the other "is to regard the spiral structure as a [quasi-steady] wave pattern", reads:
"Toomre tends to favor the first of the possibilities described above. In his point of view, the material clumping is periodically destroyed by differential rotation and regenerated by gravitational instability. 73 [...] The present authors favor the second point of view [...] Since A. Toomre's (1964) point of view has been published, it seems desirable to publish our point of view even though the work is not yet as complete as the present writers would wish to have it." (LS64, p.646)
This puzzles. Although it is true that from about 1962 onward Toomre suspected - much as Lynden-Bell had already done in his thesis two years earlier, as it turned out - that at least the more ragged-looking spiral structures result primarily from recurrent gravitational instabilities in the plainly dissipative gas layer of a galaxy (Toomre), there was no explicit discussion of any such suspicions in T64 as actually published. One cannot help but think that this accentuated mention of `Toomre (1964)' was more than just a mistaken reference, that actually it betrayed the influence that at least the cited paper had on Lin.
Shu: "Here, I can only speculate, because certainly my foresight then was not as sharply developed as Lin's. Nor was I privy to the developing estrangement between him and Alar Toomre. [...] Lin had been thinking about the problem of spiral structure nonstop since the Princeton conference in 1961. But he had a world-renowned reputation to protect and therefore was loathe to publish anything hasty before he had worked out his ideas mathematically to his satisfaction. [...] Lin (and later, I) felt strongly that spiral structure was, in essence, a normal mode. But by all the standards of what was then known, a normal mode could not be spiral (unless it grew ridiculously fast). Nevertheless, Lin felt sure that one should not do the naive thing of superimposing equal trailing and leading parts when the wave frequency is (nearly) real. And he probably wanted to discover the reason why before publishing anything. Alar's 1964 paper triggered him into premature action". (Shu)
Lin: "The urgency in my submittal of our paper was to present a different perspective, not to fight for priority". "After reviewing the paper again, I think I could not have done much better or even any better". (Lin)
One way or another, we see that by 1964 Lin indeed had had several thoughts and feelings about spiral modes, and he was eager about gaining power to his perspective. At that, he knew of a growing optimism with shearing or evolving density waves 74 and, as well, of the parallel wave-mode interest at Harvard. The T64 paper 75 , apart from its engagements on disk stability, did mention Kalnajs' advancing efforts and, still more glaringly, it also mentioned and already discussed Lin's yet unpublished solutions. 76 This must have put Lin in a position to urgently patent his views, albeit makeshift in argument for want of better mathematics, and in so doing he rather awkwardly exhibited the opponents' preoccupations as an alternative already placed on record.
3.2. A definitive (?) new prediction
| A desirable feature of the WKBJ waves is their mathematical simplicity; their physical relevance to the "grand design" of a spiral galaxy is less transparent. |
| Kalnajs 1971, p.275 |
"Just how much did Kalnajs' study of axisymmetric oscillations influence our work? The simple answer is: very little, if at all" (Lin). Such is Lin's judgment regarding the results he had set out in the summer of 1965. 77 Those got out of the printer in no less than one year (Lin 1966, 1967a), but an abridged and slightly updated version appeared as soon as February 1966, having become an "Outline of a theory of density waves" by Lin and Shu (1966), labeled `Paper II'.
The three issues reported a WKBJ-styled dispersion relation for the razor-thin hot disk,
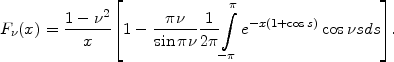 |
(17) |
From its Kalnajs' axisymmetric analog (9)-(10) it differed in the Doppler shift included in and in the form of the reduction factor F(x). 78 It was an idea of some such dispersion relation, Lin and Shu (1966) remarked, that had fed originally (LS64) their insight in the disk-stabilizing role of random motions. 79
But an important dynamical, not chronological, point was that the hot rotating disk was seen to conduct radial and spiral waves rather distinctly. Given a state of marginal stability, the oscillatory radial neutral mode = / = 0 is well maintained by it along its medium radii (dying out at large r's), 80 the local wavelength function 0(r) depending on mass and angular momentum distributions. In contrast, the spiral wave cannot be neutral as extendibly: its Doppler-shifted frequency - m(r) gets r -dependent. This ties the neutrality condition = ( - m) / = 0 to a narrow corotation zone of r rc, and there only can the interarm spacing (r) equal 0(r), the rest of disk getting more and more stable against the wave as one travels away from rc in or out. If so, why not to try to juxtapose the basic Lin-Shu concept of a balance and the solar-region stability inference by Toomre? For this, it seems sufficient to send corotation way beyond - to an outer disk region supposedly as permissive to marginal stability as to admit it - and to cancel all instability inside that rc in favor of Q 1. Lin and Shu did seem to have followed this way. Moreover, they adopted a Q 1 model (discussed already in T64), being captured by a picture of overstability, i.e. gradient instability held to mildly develop over the system and to provide some selective amplification of trailing, not leading, waves.
Besides, relation (17) tells (k) to decrease with wavenumber till k remains under some k0, and then to rise up at k back to unity. Any intermediate value of is met thus twice, meaning two branches of WKBJ solutions, the shorter- and the longer-wave ones, their forms r() being provided by equation (16) with F(x) added in the integrand denominator. If Q 1, the branches join at corotation, showing there equal interarm spacings sw(rc) = lw(rc) = 0(rc). This value is the largest (smallest) for the shortwave (longwave) branch: sw(r) falls down until zero (lw(r) ) as one goes from corotation to ILR. Aimed from the outset at explaining the observed 2-3 kpc local spacings, Lin got tempted to acknowledge the shortwave branch, the more so as, not to forget, in 1964 he had had no choice when having to comment on this same gas-given spacing on the basis of relation (14) that seized but one - long-wave (!) - branch. 81 But things did not get all as clear by 1966, and this is why neither Lin (1966, 1967a) nor Lin and Shu (1966) were eager to go into the wave-branch question, keeping silent about any graphic view of their newer formula. Only at the Noordwijk IAU Symposium (August, 1966) they gave a graph, it displayed the short-wave-branch extension of the () curve (Fig.10) on which they built a model for the full spiral of our Galaxy (Fig.11), tentatively two-armed and answered by a remote corotation (Lin & Shu (1967). 82 Spirals of this class show as slow a rotation as to almost guarantee the ILRs be present and lie in a relative proximity from the center. Namely, Lin and Shu connected our `home' m= 2 ILR with the `3-kpc arm' which fixed the spiral pattern speed p = 11 km/s/kpc.
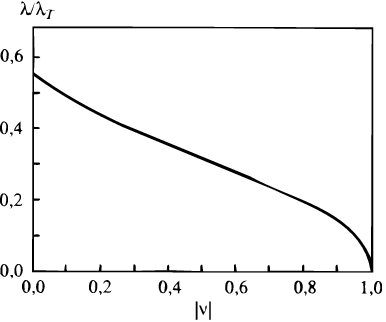 |
Figure 10. The short-wave branch of the dispersion relation (17) for a Q = 1 disk model. (The figure is reproduced from Lin & Shu 1967) |
 |
Figure 11. The Lin-Shu model for the Galactic spiral density wave. The model is calculated with the help of the dispersion curve in Fig.10. The dashed line shows the ILR region taken to be the residence of the `3-kpc arm'. This provides the pattern speed p = 11 km/s/kpc. (The figure is reproduced from Lin & Shu 1967) |
"My earliest recollection of realizing that there were separate long and short branches came when I was doing the numerical calculations for the spiral pattern that Lin wished to show at the Noordwijk symposium. As I recall, he was in the Netherlands and I remained behind at Harvard, and we corresponded by mail. I was considerably confused by which of the two branches should be used to generate spiral patterns (I had realized that a `reduction factor' applied to our 1964 formula was an incomplete description, and that long and short waves were implicit to Toomre's evaluation of a critical Q for axisymmetric disturbances). Finally, Lin suggested that we should simply choose the short branch by fiat as the practical thing to do given the press of the Noordwijk presentation, and we were left to try to sort things out later. That's my memory of the events". 83 (Shu)
The Noordwijk diagram has been the first presentation of our Milky Way's density wave.
63 Lin's basic themes still were in hydrodynamics (e.g., Benney & Lin 1962; Reid & Lin 1963). Back.
64 That criticism (Chandrasekhar 1942) concerned only the asymptotic-spiral theory, and it was itself not flawless as attached to confusing empirical data of the 1920's - 30's. Back.
65 "I have been thinking of modes ever since I learned about the fine points of the Hubble classification". (Lin) Back.
66 "I adopted the empirical approach because of my close contacts with the observers (and with Lo Woltjer). Now that I have thought over the situation some more, I think I should admit that it is probably true that my past long-standing experience in the studies of hydrodynamic instability did (as you hinted) play a role in my thinking (although I was not conscious of it). But more important, I also feel (upon reflection) that the reason I adopted the empirical approach is really the natural consequence of my past education. My undergraduate education was in physics (at Tsinghua University of China, where all the major professors in Physics had doctorate degrees from English speaking universities such as Harvard, Caltech, Chicago and Cambridge), with all the pleasant memories of doing the experiments with precision and the satisfaction of having the data checked against theory. My graduate education was primarily at Caltech where I studied under Theodore von Karman. It is also there that I took a course from Fritz Zwicky who first identified the regular spiral structure in the Population II objects of the Whirlpool M51". (Lin) Back.
67 "Despite of my decades of experience with instability of shear flows, I did not bring these matters into the presentation of the 1964 paper, but commented only vaguely about instability. [...] There was no shortage of theoretical astronomers who understood the mechanisms perhaps better than I did; e.g. Lo Woltjer and Donald Lynden-Bell and perhaps even Peter Goldreich (even at that point). Goldreich turned out be the most successful leader in the understanding of the density waves in the context of planetary rings". (Lin) Back.
68 "In hindsight, I think Lin's judgment was accurate considering how quick people were to attack his point of view with proofs of `antispiral theorems' and the like shortly after the publication of LS64". (Shu) Back.
69 "All the original ideas were C.C. Lin's, and my original contributions were mainly to check the equations that he wrote down and posed as problems. (I did find a way to derive the asymptotic relation between density and potential by attacking the Poisson integral directly, but even there I initially blundered in not realizing the necessity of an absolute value on the radial wavenumber. The final derivation presented in the appendix of LS64 is due to Lin). I did considerable reading, however, on the astronomical side and may have contributed some ideas concerning how OB stars form and die in spiral arms. (This was the beginning of my lifelong interest in star formation.) Lin was indeed quite generous to include me as a coauthor on LS64, and I will always be grateful for his guidance and support of a young (I was 19 at the time) undergraduate student". (Shu) Back.
70 "Lin undoubtedly encouraged many of his younger colleagues - like Alar Toomre - to think about the problem of spiral structure. I can only imagine that Lin's treatment of people then much more junior than himself was equally as generous as his treatment of myself. Certainly, he must have discussed with Alar Toomre (and later Chris Hunter) his ideas about this problem. Toomre's early papers on the subject acknowledge this debt of introduction and inspiration. Why then did those early papers not carry Lin's name as a coauthor? I do not know, nor would I dare to probe (by asking either Lin or Toomre) for fear of opening old wounds that are best left closed". (Shu)
One way or another, no alliance was formed between Lin and Toomre. They "diverged in emphasis from the very beginning", so that "there were discussions, but no real collaboration" (Lin). As in agreement with this Toomre recalls that back again at MIT in spring 1963 he did decline Lin's "astonishing suggestion to write some such paper jointly, since he himself had contributed almost nothing very concretely to my gravitational (in)stability insights, and yet also since I likewise felt I had added next to nothing to his own spiral-wave hopes" (Toomre). Back.
71 That the historical Lin & Shu article was referred to as `Lin's (1963) preprint' by Layzer (1964) and as `Lin (1964)' by Toomre (1964) and Kalnajs (1965) as it was about to appear in the fall of 1964 speaks of its urgently extended coauthorship as Lin's last moment decision (so striking for a well-motivated and ambitious scientist).
Anyway, the Lindblad (1964) paper, also considering quasi-stationary circulation and the resulting spirals in differentially rotating galaxies, appeared half a year prior to Lin's patent. The authors had neither contacts nor fresh news on each other's most parallel work, and hardly could have it. "There was no justification to trouble B. Lindblad with a novice being converted, Lin explains. I was waiting for a definitive new prediction before writing to him. Even then I would have done it through P.O. Lindblad for several obvious reasons. Unfortunately, by the time our result came out (IAU Symposium No 31) [see Sect.3.2] he already passed away" (Lin). Even less probable was any contact-making step from the other side. "About that time [fall of 1964] my father was on a trip around the world caused by the inauguration of the Parkes telescope in Australia, P.O. Lindblad recalls. On his way home he passed through the US [...] but he brought no news about density wave theories. [...] I think my father was aware of the existence of the LS64 paper but had not had the time to penetrate it. I know that he was happy to learn from Whitney Shane, who visited us around the beginning of June 1965, that his work on spiral structure had been more and more appreciated recently". (P.O. Lindblad) Back.
72 To soundly fit the empirical 2-3 kpc local-arm spacing in the Milky Way, LS64 chose a combination of angular speed p = 10 km/s/kpc and growth rate = 50 km/s/kpc (!) for their tentative two-armed spiral. Back.
73 "The prevalent thinking among the other prominent theorists of the time - and this included Alar Toomre - was that spiral structure was a chaotic and regenerative phenomenon - `shearing bits and pieces', as Alar later put it in one of his papers". (Shu) Back.
74 Goldreich and Lynden-Bell in England and Julian and Toomre at MIT set to work on this by 1964. Back.
75 The revised version of T64 was submitted in January 1964. Back.
76 Toomre concluded that "whatever differences there may exist between the shorter axisymmetric and non-axisymmetric disturbances, these must in essence be due only to the circumstance of differential rotation" (T64, p.1223). In Lin's hands, in contrast, this `circumstance' still allowed the dispersion relation (14) for non-axisymmetric waves to be rather close to its axisymmetric analog (5), although the waves stood as steady-mode solutions of the WKBJ type. Yet, as well, the governing equations admitted an "altogether different family of approximate non-axisymmetric solutions" (T64, p.1223), with the radial wavenumber proportional to the disk shear rate A(Oort's constant), and growing with time, kr At. This meant that a spiral disturbance of the leading form (t < 0) unwrapped, started trailing, and then wrapped tighter and tighter (t > 0). Thus the point was that, on the one hand, differential rotation continuously deforms even the tightly-wound spiral waves of this sort, whereas, on the other hand, these "should probably be regarded as particular superpositions of Lin's solutions" (T64, p.1223). This discordance was thought to be removed by a fuller analysis beyond the WKBJ-limit. Back. ###
77 Lin presented his first hot-disk results in June 1965 at a summer school at the Cornell University and at a mathematical symposium at the Courant Institute. These materials were published in two extensive articles (Lin 1966, 1967a) submitted in July. "I recall becoming aware of the relationship with the work of Kalnajs only when he brought up the issue in connection with Frank Shu's thesis presentation. I immediately recognized that there would probably be a way to make the connection through the application of the Mittag-Leffler theorem. Note that it is easy to derive the Kalnajs form from our integral form, but difficult to reverse the process. And our numerical calculations depended on the simple integral, since it was a time when large scale use of the computer was not yet available in a mathematics department. (I still remember the painful experience when my request - as chairman of the committee on applied mathematics - for a computer was turned down, even though the department had the funds. [...] Kalnajs might have been able to check the calculations with his infinite series through the use of the computer.)" (Lin) Back.
78 "I have little knowledge but I make this conjecture: Kalnajs was studying axisymmetric oscillations, not standing waves of the spiral form, and obtained his results through the use of results for analogous oscillations in plasma waves. (I learned a lot about plasma physics only after Y.Y. Lau joined our research group.)" (Lin) Back.
79 Lin agreed that the dispersion relation was already derived by Kalnajs "in the special case of axially symmetrical disturbances", but "by a quite different method" and "independently of the work of the author" (Lin 1966, p.902). He certainly appeared rather sensitive on the point of independence, beginning his spiral studies. His first appraisal of Lindblad's long-term emphasis on steady spirals was: "Indeed, independently of each other, B. Lindblad (1963) and the present writer came to the same suggestion of a quasi-stationary spiral structure of the stars in a disk galaxy" (Lin 1966, p.898). Again, referring time and again to different methods adopted by him and his various competitors, Lin found it difficult to closely compare those related issues. But, for example, Lynden-Bell (1962) and Toomre (1964) had used the same characteristics method as that taken in 1965 by Lin, with which he basically re-derived, again independently, this time from Toomre, that crucial differential equation of `asymptotic' disk-stability and density-wave theories (cf. Eqn (53) from T64 with Eqn (7.15) in Lin 1966 and Eqn (A20) in Lin et al 1969), not having mentioned its factual use by his next-door institute colleague. Back.
80 Such behavior is well seen on Fig.3 from T64 showing results of numerical calculations of global radial modes for some illustrative cold-disk model. Back.
81 LS64 had assumed that because not all the stars but only those with smallest random velocities perceptibly contribute to the response of a disk, its effective surface density must be several times less than its full value. Back.
82 "This was my first meeting with the distinguished astronomers who made all the important observations related to spiral structure, many of whom worked under Oort's direction. Here we presented our first prediction of the spiral structure of the Milky Way, which remained to be an approximate representation, as indicated by Yuan's continual refinement over the years". (Lin) Back.
83 "Lin and Shu 1966 emphasis upon (and the dispersion relation for) the short-wave branch of nearly axisymmetric WKBJ-style density waves, which is something that Kalnajs (1965) also knew from his thesis but failed to emphasize nearly as adequately, escaped me altogether even though the same for the long-wave branch as well as the stability criterion were plain as day from T64 - and to a more limited extent even from Safronov (1960a, b), as I often agreed in retrospect. I think my trouble was that my own ongoing work then with Julian (Julian & Toomre 1966) [...] had also sensitized me to the severity of phase mixing. [...] Looking back, this made me suspect until well into 1965 that all short stellar-dynamical waves, unlike their over-idealized gas equivalents, would in fact be strongly damped and were probably not of much value. And right there I have cheerfully agreed for about 34 years now that Lin and Shu (and as an independent authority also Kalnajs, not at all to be omitted) together proved me to have been spectacularly wrong". (Toomre) Back.
<< 2. On a New Wave Crest | Contents | Afterword >>
|
Публикации с ключевыми словами:
история астрономии - спиральная галактика - волны плотности - спиральная структура
Публикации со словами: история астрономии - спиральная галактика - волны плотности - спиральная структура | |
См. также:
Все публикации на ту же тему >> | |