1. LINDBLAD'S ERA
| The only result that seems to emerge with some clearness is that the spiral arms are permanent features of the nebulae [...] perpetuated in static form. |
| Jeans 1929, p.360 |
1.1. From unstable orbits to global wave modes
| It is natural that in this field, on which at that time nothing was ripe for harvesting, he did not immediately find the right path. |
| Oort 1967, p.333 |
Though the fact of our larger-scale universe had begun to emerge through Hubble's work, it was not yet as clear on the quantitative side: well advanced in rank, the `nebulae' still came short of size and mass against our Galaxy. This was made by the underrated galaxy-distance scale, 5 and the giant ellipticals, missing in the Local Group and nearby, got it the most. On the whole, the ellipticals were found to be one to two orders under the spirals, and the rather enigmatic barred galaxies were ranged somewhere intermediate (Hubble 1936).
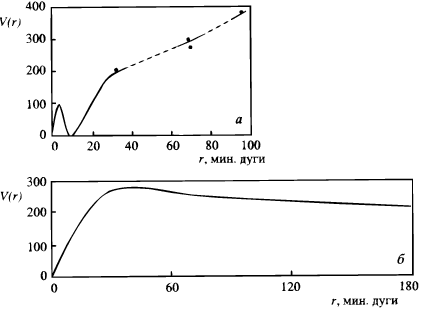
Original absorption-spectrum methods of detecting the galaxy rotation were sensitive only for bright central regions of comparatively close systems, the line inclination being established integrally, as a quantitative measure of overall uniform rotation. The emission-spectrum methods, in practice since the late 1930s, could as well catch the kinematics of the rather distant regions in our next-door spirals M31 and M33 (Babcock 1939, Mayall & Aller 1942). Limited and inaccurate though these data were (Fig.1), they took astronomers by storm and for almost two decades then they formed and served the idea of a standard rotation curve. The latter was understandably professed to obey V(r) = ar / (1 + b r2) and be scaled so as to co-measure its rising part to a live galaxy within its `visible boundary'. 6,7 And on the barred spirals it was disarmingly clear "with no measurement" at all that in face of rapid bar destruction their rotation was nothing, if not uniform (Ogorodnikov 1958, p.517).
 |
Genuinely matched with the empirical climate were the theoretical tastes of the epoch that followed closely Jeans' directive on unified cosmogony of galaxies and stars. 8 One relied on the study of gaseous figures; they were diagnosed to be open to evolutive secular instability created by dissipation factors acting in the steady-motion systems. The latter just "never attain to a configuration in which ordinary [dynamical] instability comes into operation" (Jeans 1929, p.199), so that "it is secular stability alone which is of interest in cosmogony" (Jeans 1929, p.214) 9 . Quite understandably, Lindblad's early work lay nearby in the feeling for global evolutionary processes. 10 Yet he was the first, and for more than thirty years almost the only one, who singled out the spiral problem and treated it as a separate, stellar-dynamical element in the general philosophy of galaxies. 11
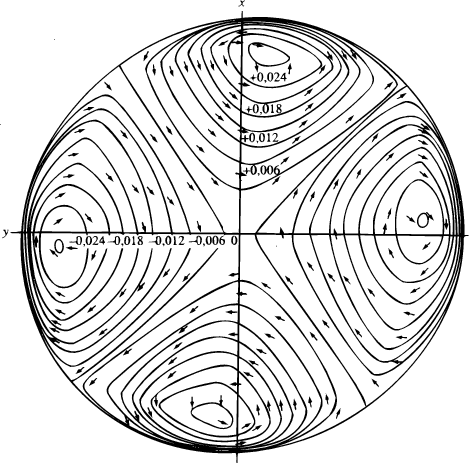
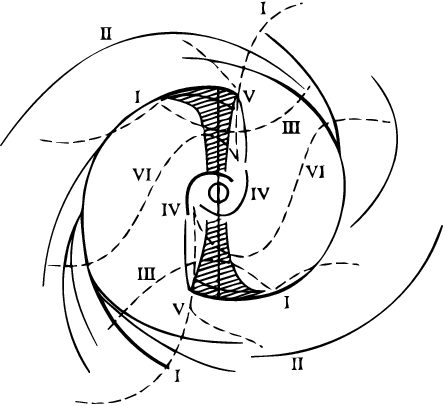
Lindblad started from a highly flattened lens of stars in uniform rotation ( = const, A = 0 in Eqn (1)) created in the course of primary evolution (Lindblad 1926a, 1927a). Gravitational potential at its edge changes so abruptly with radius that circular orbits there get unstable (2 < 0): those inside of, but close to, the edge need only a slight individual change in energy in order to be transformed into quasi-asymptotic orbits extending very far from the `mother system' (the solar neighborhood belongs exactly to some such exterior that shows differential rotation obeying relations (1)). Still stars leave and return to their mother system spontaneously and equiprobably in any point on its edge, which is not conducive to neat global patterns. But the hitch is removed upon the admission of either an outside disturber or an overall oval distortion caused by fast rotation. 12 In both cases, two opposite ejection points arise on the edge of the lens after a transitory process and, fixed in space, they pour material out in spiral-looking leading gushes. Turning to intrinsic mechanisms of galaxy structures, Lindblad laid greatest stress upon global modes of disturbances, called the deformation waves (`uncompressible' modes) and the density waves (`compressible' modes), and sought their unstable solutions (Fig.2). 13 Analyzing the effects such waves had on stars on asymptotic orbits (Fig.3), he proposed and refined scenarios of spiral-arm formation in an outer, shearing galaxy envisaged to keep up somehow the patterns as arranged by a mass of the affected orbits, rather than to destroy them (Lindblad 1927a, 1948, 1953). 14,15
 |
 |
| The difficulty of cosmogonical theories lies in the interconnection of the facts. |
| Weizsacker 1951, p.165 |
| Where a few years ago we seemed to be up against a blank wall of discouragement, we are now in an era of rapidly developing research. |
| Bok & Bok 1957, p.244 |
Stellar dynamics of the 1940s - early 1950s was essentially the theory of a stationary galaxy arranged by the regular forces (see Ogorodnikov 1958) and the theory of quasi-stationary systems open to slow relaxation processes (Ambartsumian 1938; Chandrasekhar 1942, 1943). Together, they provided a basis serving well for getting certain practical dividends but still of little use for conceiving the underlying dynamical problems.
"While these methods have contributed substantially toward the clarification of the peculiarly characteristic aspects of stellar dynamics, an impartial survey of the ground already traversed suggests that we are perhaps still very far from having constructed an adequate theoretical framework in which the physical problems can be discussed satisfactorily. In any case we can expect that the near future will see the initiation of further methods of attack on the problems of stellar dynamics" (Chandrasekhar 1942, p. vii-viii). 16
The envisaged future did not happen to lie as immediately near, however. The theoretical thought kept on whirling around the idea of galaxies evolutionarily tracking over the Hubble diagram, one way or the other, and that opened in quite a few attempts at a synthesis of the available strict knowledge about gravitating figures in a softer (then bulkier) spirit of cosmogonical inclusion. 17 Accordingly, non-stationary - dynamical - problems of deformation of the systems and of density disturbances in them seemed difficult and therefore premature, while stationary problems were held as "natural and necessary" at that preliminary point, for "it is hard to imagine that at all stages the evolution of stellar systems has the violently catastrophic character" (Ogorodnikov 1958, p.13). 18 In this illumination, Lindblad's theory of unstable bar-modes was typically deemed extravagant and unacceptable (Lebedinski 1954, p. 31).
"Such theories cannot yet help the progress of cosmogony, since uncertainty in them still prevails validity" (Schatzman 1954, p.279).
The delicacy of this sort of expert judgment - let alone its other virtues - reflected clearly that it was the issue of gas and dust that became a common focus of galaxy astronomy despite its stellar past. 19 By the 1950s, Baade discovered in M31 many hundreds of emission nebulosities (HII regions), having concluded that "they are strung out like pearls along the arms" (Baade 1963, p.63). Gas and dust, he stated, are also distributed in this galaxy highly unevenly, grouping in its spiral arms. 20 Besides, no one already doubted the youth of high-luminosity stars since they were ascertained to still form in abundance, e.g. in the Orion nebula. The sheer weight of these individually weak facts convinced many workers that
"the primary phenomenon in the spiral structure is the dust and gas, and that we could forget about the vain attempts at explaining spiral structure by particle dynamics. It must be understood in terms of gas dynamics and magnetic fields" (Baade 1963, p.67). 21
The lion's share of these discoveries was made possible due to the 200-inch Palomar reflector put into operation in 1949, although from 1951 onwards the interstellar gas was unprecedentedly attacked also by the 21-cm-line methods. Dutch radio astronomers presented "one of the truly historic diagrams of Milky Way research" (Bok & Bok 1957, p.244) - a detailed map of atomic hydrogen distribution (Hulst et al 1954). 22 It displayed extended fragments of tightly-wrapped spiral arms which in the solar vicinity matched `local arms' in Sagittarius, Orion and Perseus. 23 Gas kinematics routinely analyzed, a synthesized rotation curve of the Galaxy was pictured (Kwee et al 1954), and the "primary task for the next few years" was claimed to get improved radio equipment "capable of tracing with precision the spiral structure of our Galaxy".
"While there is always room for theorizing, the emphasis must first of all be on careful observation and unbiased analysis of observations" (Bok & Bok 1957, p.248).
The new empirical facts - the tightly wrapped, nearly ring-like arms of the Milky-Way spiral, the concentration in them of Population I objects, the general shearing character of rotation - were a surprise to Lindblad. He could not neglect them. But they demanded another, more fitting dynamical theory, and Lindblad put aside (but did not deny 24) his business with unstable circular orbits and wave bar-modes. This step was largely favored by first numerical experiments in galaxy dynamics performed in 1955-60 by his son P.O. Lindblad with the big electronic computing machine installed in Stockholm (Lindblad & Lindblad 1958; P.O. Lindblad 1962). Those experiments showed the trailing - not the leading - spiral arms, the ones supported by fresh data on both the form of the Milky-Way spiral and the space orientation of many galaxies (de Vaucouleurs 1958), and, after all, the ones put into orbit way back by Hubble (1943) in the framework of his working hypothesis that galactic spirals always trail. 25
| The spiral structure is nothing more than a tracer element contained in a fairly uniform disk of material [...] This is probably related to the magnetic field in the disk. |
| G. R. Burbidge 1962, p.295 |
| As far as I am aware, no single problem, not even a stability problem, has been solved in a differentially rotating self-gravitating medium. Even without magnetic fields, and even linearizing the equations, it is very hard to make progress. |
| Prendergast 1962, p.318 |
| With our observations we have reached a point where we are simply unable to draw any definite conclusion, unless the theory helps us. I hope some day there will be action, because otherwise we are lost. |
| Baade 1963, p.266 |
The post-war success in galaxy research gave priority to the empirical approach. By the late 1950s, it formed two flanks of evolutionary studies, morphological and quantitative. The first one, due mostly to the Palomar sky survey, called for elaborate classifications, catalogs and atlases of galaxies (Zwicky 1957; Morgan & Mayall 1957, de Vaucouleurs 1959; Vorontsov-Velyaminov 1959; Sandage 1961); the second exploited matters concerning stellar evolution and empirical data on individual galactic objects. As regards the theoretical approach, it too branched under the new conditions and its subject was now treated in distinct frames of physical, chemical and dynamical evolution.
On this dynamical side, the one to our present interest, true lodestars started shining by the 1960s. One of them was lit by the linear stability theory as applied to long-range force systems; denied so far, mostly by human inertia, its methods eventually penetrated into the galaxy dynamics. 26 Chandrasekhar (1953, p. 667) formulated the problem as follows:
"When we know that an object has existed in nearly the same state for a long time we generally infer that it is stable; and by this we mean that there is something in its construction and in its constitution which enables it to withstand small perturbations to which any system in Nature must be subject. [...] Thus when we are confronted with a novel object - and most astronomical objects are novel - a study of its stability may provide a basis for a first comprehension".
To him, however, it was a matter of pure intellectual interest, above all. "For an applied mathematician, Chandrasekhar explained, problems of stability present a particular attraction: by their very nature, these problems lead to linear equations and linear equations are always more pleasant to deal with than nonlinear ones" (Chandrasekhar 1953, p.667). 27 In so thinking, he turned to most general, technically transparent models. One of such was Jeans' infinite homogeneous medium asked about whether the classical stability criterion k2 c2 - 4 G > 0 and the critical fragmentation scale J = ( c2 / G )1/2 remain unchanged if the medium is involved in uniform rotation (ñ and are sound speed and material volume density; k, and = 2 / k - wave number, frequency and length; G -gravity constant). 28 The answer came positive, with the one exception for perturbations propagating in the direction just at right angles to the rotation axis, when Coriolis force co-governs wave dynamics and modifies the dispersion relation into
| (2) |
showing that any rotation with > ( G )1/2 entirely prevents the system from decay.
Safronov (1960a, b), interested in protoplanetary cloud dynamics as a part of his solar-system cosmogony, examined a more realistic model - a differentially rotating gas layer stratified along the rotation axis. 29 A short-wave analysis led him to a relation
| (3) |
that basically differed from Eqn (2) in its modified gravity term depending on both wavenumber and the layer's thickness h. The correction factorf (k,h) evaluated, Safronov found - quite in Jeans' spirit - that rotating flat systems lose stability and must break up into rings as soon as their equilibrium volume density gets above some critical value.
In that same 1960, first results were supplied by collisionless collective dynamics, concerning the simplest, spherical systems. 30 Antonov (1960) found for them the now classical "stability criterion, rather complicated though", and Lynden-Bell (1960a) discovered a peculiar feature of their equilibrium states - the ability of collisionless spheres to rotate. 31
Another lodestar for dynamical studies was the evidence provided by a bulk of higher-precision rotation curves obtained for spiral galaxies in the late 1950s by Burbidges and Prendergast. At long last, their general rotation was ascertained to be strongly differential. This fact, stripped now of all surmise, seriously warned astronomers that they were in the presence of a real problem of the persistence of spiral structure.
"There appears to have been some feeling in recent years that individual spiral arms are long-lived features in a galaxy. [...] However [...] we shall show that the form of the rotation-curves for spirals will insure that the spiral form will be completely distorted in a time short compared with the age of a galaxy" (Prendergast & Burbidge 1960, p.244).
The quantitative estimates did show that the data on M31, M81, NGC 5055 "and probably all similar spiral galaxies" were in conflict with "certain apparently reasonable assumptions" - namely, at least with one out of the following three: (a) only circular velocities are present in galaxy disks, (b) these velocities are independent in time, (c) material which is originally in a spiral arm remains in that arm (Prendergast & Burbidge 1960, p.244, 246).
The `urgent problem' of the persistence of spiral forms was taken up by Oort. Speaking at a 1961 conference at Princeton of "every structural irregularity" in a galaxy as being "likely to be drawn out into a part of a spiral", he called for another phenomenon to turn to and conceive:
"We must consider a spiral structure extending over a whole galaxy, from the nucleus to its outermost part, and consisting of two arms starting from diametrically opposite points. Although this structure is often hopelessly irregular and broken up, the general form of the large-scale phenomenon can be recognized in many nebulae" (Oort 1962, p.234).
Oort suggested "three ways out of this difficulty", one of which was that "the arms could retain their present spiral shapes if matter were constantly being added to their inner edges, while the outer edges would constantly lose matter" (Oort 1962, p.237-8). This possibility was given an eager discussion at the conference (Oort 1962, p.243).
Yet one more lodestar for galaxy dynamics was lit in the 1950s by numerical computer methods. They first served the calculating of three-dimensional star orbits; Contopoulos (1958, 1972) then stated their non-ergodicity and posed anew the problem of a third integral of motion. P.O. Lindblad, as we saw, turned the same Stockholm computer to studying the galaxy dynamics in terms of an N -body problem (Lindblad & Lindblad 1958; P.O. Lindblad 1962).
| Most remarkably after that fine beginning [in 1925-27], it took Lindblad not three further months or years, but three whole decades, to connect this implied epicyclic frequency and the ordinary angular speed of rotation Ω into the kinematic wave speeds like Ω ± κ/m, which we very much associate with him nowadays, especially when muttering phrases like "Lindblad resonances". |
| Toomre 1996, p.2-3 |
These fresh winds did not catch Lindblad unawares. The importance of differential rotation was already conceived by him from radio observations (Kwee et al 1954; Schmidt 1956), and he even noticed - for the Galaxy and, later, for M31 (van de Hulst et al 1957) and M81 (Munch 1959) - the curious empirical near-constancy of a combination
| (4) |
And the dynamical stability problems were always comprised by his spiral theories. Already from 1938 on, dispersion relations of type (3) surfaced in his evolving papers, growing more and more complicated by way of various gradient-term inclusions for a tentatively better description of the crucial - unstable - bar-mode (see Genkin & Pasha 1982). 32
However, the idea of applying the collective-dynamical methods to shearing stellar galaxies hardly ever impressed Lindblad. He must have felt (Lindblad 1959) the limits of his hydrodynamical approach (long-wave solutions at differential rotation were unattainable analytically, while, on the short-wave side, the whole approach failed for want of an equation of state), not having yet a means of solving kinetic equations. Also, Lindblad perhaps doubted the very possibility of steady modes in shearing galaxies. Either way, the empirical relation (4) that he himself had stated inspired him the most. With it as a centerpiece he started a new, "more definite theory of the development of spiral structure" (Lindblad 1962b, p.148), one he called the dispersion orbit theory (Lindblad 1956, 1961). It was imbued, intuitively, with a hope that gas and Population I stars "are somehow aggregated on their own into a few such orbits in each galaxy - almost like some vastly expanded meteor streams" (Toomre 1996, p.3).
Lindblad described epicyclic stellar oscillations in a reference system rotating with angular velocity n = - / n, n = d / d, and he imagined a star's radial displacement to depend on its azimuth as cos n( - 0), 0 being apocentric longitude. The simplest forms of orbits occurred for integer n's, the case of n = 2 satisfying the empirical condition (4). For this case, "the most general form of an ellipsoidal distribution with vertex deviation" was obtained (Lindblad 1962b, p.152), with which Lindblad sought to calculate the total gravitational potential and, by extracting its averaged (over time and angle) part, to treat the remainder as a contribution to the perturbing force. He Fourier-decomposed this force and retained the m = 1, 2 harmonics to analyze disturbances to a ring of radius r composed of small equal-mass particles. Like Maxwell (1859) in his similar Saturn ring problem, 33 Lindblad obtained four basic modes for each m. Two of them described nearly frozen, practically co-rotating with material, disturbances to the ring density. Two others - "deformation waves" - ran with speeds ± / m, the minus sign being for the slower mode. It was, at m = 2, "essentially this slowly advancing kinematic wave [...] composed of many separate but judiciously-phased orbiting test particles" (Toomre 1977, p.441) that Lindblad meant by his dispersion orbit (). The fact that its angular velocity was independent of radius, p(r) = 2 = const (with an observational accuracy of the condition (4)), implied a stationary state for all test rings, i.e. over the entire radial span where this condition was well obeyed.
"This fact greatly intrigued Lindblad - who did not need to be told that strict constancy [of p(r)] would banish wrapping-up worries or that the nicest spirals tend to have two arms. Yet astonishingly, that is about as far as he ever got. [...] It never occurred very explicitly to [him ...] to combine already those `orbits' into any long-lived spiral patterns" (Toomre 1977, p.442).
1.5. Circulation theory of quasi-stationary spirals
| The suggestion that the patterns are density waves is old and was first explored by Bertil Lindblad. His emphasis was mainly on kinematics and less on collective effects on a large scale, though many of the kinematical effects he discovered can still be seen in the collective modes. |
| Kalnajs 1971, p.275 |
| His details were unconvincing, but no one can accuse him of missing the big picture. |
| Toomre 1996, p.3 |
P.O. Lindblad's experiments with flat galaxies were planned to clarify the dispersion-orbit theory. They started with a plane system of several annular formations arranged by N 200 mutually attracting points, and the development of "small deviations in shape and density of a bisymmetrical nature" (Lindblad 1963, p.3), applied to one of the rings, was studied. Two waves propagating along it were shown to rise first, one running slightly faster and the other slower than unperturbed particles, thus invoking a pair of corotation resonances, one on each side from the ring. These induced a leading spiral; soon it rearranged into a trailing one and smeared out almost completely, but some trailing arms then re-appeared, owing evidently to a small oval structure retained at the center. This led P.O. Lindblad to propose that galactic spirals may involve a quasi-periodic phenomenon of trailing-arm formation, breakup and re-formation. 34
B. Lindblad, however, got captivated by another view of these results. He even lost of his earlier dispersion-orbit enthusiasm and turned in 1961-62 to a concept "On the possibility of a quasi-stationary spiral structure in galaxies" (Lindblad 1963) in the presence of differential rotation. 35
"The morphological age of spiral galaxies as estimated [...] from considerations of the evolutionary process connected with star formation from gaseous matter ranges between 109 and 1010 years. In consequence it is natural to assume that the typical spiral structure is not an ephemeral phenomenon in the systems but has a certain steadiness in time [...and] to investigate how far gravitational forces alone can explain a spiral structure of a fair degree of permanence" (Lindblad 1964, p.103).
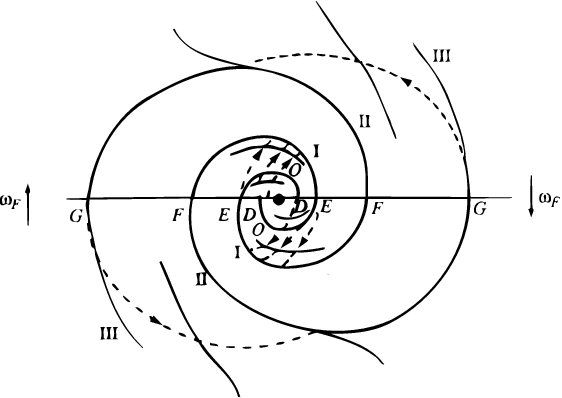
To begin with, Lindblad introduced an axisymmetric flat stellar system in differential rotation and, echoing the N -body pictures, imposed on it an initial trailing spiral pattern formed by some extra amount of stars. His calculations of the effect upon a nearby test star from such a spiral arm showed that, as it sheared, the star approached it and fell in, having no other chance to leave it than making slight epicyclic oscillations. Such an assimilation of material in just one galactic turn or so worked well against shearing deformation of spiral arms, through their exchange in angular momentum with stars attracted. As the result, the pattern's angular speed became the same all over, meaning its quasi-stationarity. Now two dynamically different regions arose in the system, an inner region with stars moving faster than the spiral, and an outer one, tuned oppositely; they were divided by a corotation region, where the material orbits at nearly the same rate as the pattern.
For a true stationary pattern not only its permanence in shape was needed, but also a balance of the stars' travel in and out of the arms. The latter was secured in Lindblad's eyes by his circulation theory (Lindblad 1963, 1964) developed in the framework of a trailing two-armed spiral model, each arm making one full convolution (or a bit more), comparably inside and outside corotation (Fig.4). Actually, each arm ended where, according to analytical estimates, its stars were effectively attracted by the next-to-last arm (outside corotation) and fell in it "in a shower of orbits". The assimilated stars kept moving slower than the spiral, thus having an along-arm ascent until a repeated flow down. Inside corotation (the region of much less interest to Lindblad), the circulation was set up as well, but in the opposite direction: stars captured by spiral arms got drawn down along them until sucked upward by the next-to-innermost spiral convolution.
 |
This circulation theory was nothing but a sketch by 1964. Well treating quasi-steady spirals as a density wave, it gave no desired quantitative results regarding pattern speeds, arm pitch angles, interarm spacings, or the like. It also failed to explain dynamically the preference for trailing arms - although the dispersion-orbit theory had honestly done no better. It is regrettable that Lindblad, who died in 1965, did not have the time to complete this last work he had started, and only "left behind a long handwritten unfinished manuscript that in great mathematical detail studies the gravitational effects of spiral arms in his circulation pattern" (P.O. Lindblad).
The original spiral theories by Bertil Lindblad passed into oblivion. Among the causes for the passage were the feeble empirical base of the 1920s-40s, the frightening bulk of mathematics and scant help from the first computers even during the 1950s, a constant flux of changes in Lindblad's latest inferences and the rather opaque prose of his abundant articles, 36 and above all a lack of quantatively checkable predictions. Yes, one can readily agree that
"all problems that in later developments turned out to be important in the theory of spiral structure had, in one way or another, already been touched upon or even studied by Lindblad" (Dekker 1975, p.18)
as well as that
"such complex collective dynamics was perhaps too hard for anyone, no matter how talented, in those mid-20th-century decades before computers, plasma physics, or any inkling of massive halos" (Toomre 1996, p.3).
but also true is that all of the spiral undertakings by Lindblad, however ingenious and farsighted they may appear to have been in retrospect, got sunk ingloriously in the silence of time.
An interesting question is: why? Why did it come to be that the true master of theory and observation had long been surprisingly close to but never quite at the point of recognition - opened in the 1960s to a pleiad of fresh theorists - that spiral structure is mainly a collective wave phenomenon in shearing galaxies? One can only suppose that Lindblad did not reach, let alone exploit, such wave-mechanical ideas partly because they were not in the air yet, but perhaps mainly because he was impeded by his life-long emphases on the orbits of individual particles. All his efforts on galaxy dynamics were fed by the stellar-epicycle concept, the pearl of his scientific youth. This set the trend for Lindblad's theories, and whenever some such orbital attack fell short of its destination, he did not get on with searching for totally different ways of continuing, but instead renewed his attack time and again under his old epicyclic-orbit colors.
5 It was not until the early 1950s that the distance scale was reconsidered (see Baade 1963, Efremov 1989) and the size of the Local Group doubled. Given the shifted zero-point in the Cepheid-luminosity calibration, Hubble's constant was reduced, and by the 1960s it fell from its original 550 km/s/Mpc down to 180 (de Vaucouleurs) or to 80 (Sandage). This gave a 3-to-7-fold increase in distance. Back.
6 This form of V(r) emerged from the solution of Jeans' problem for an axisymmetric stationary stellar system with ellipsoidal velocity distribution. It greatly encouraged work on modeling the three-dimensional gravitational potential and mass distribution in the Galaxy (Parenago 1950, 1952; Kuzmin 1952; Safronov 1952; Idlis 1957). Back.
7 "Both in M31 and M33 the easily visible spiral arms lie in regions where the rotation does not deviate strongly from uniformity. It is remarkable in M31 that outside the nucleus [...] there is another region of nearly uniform rotation" (Weizsacker 1951, p.179). Vorontsov-Velyaminov (1972) was still confident that near uniform rotation was the type adopted by most of spiral galaxies. Back.
8 The idea of an overall one-time star formation early in the life of our Galaxy had long been predominant. In the late 1930s only the hydrogen-to-helium-synthesis energy source was proposed. That allowed evaluation of the fuel exhaustion time at a given star luminosity, and its shortness for the blue supergiants - 107 yrs - exhibited star formation as an ongoing process. This idea gained empirical support during the 1940s. Back.
9 In Jeans' view (Jeans 1929, p.213), as a nebula in uniform rotation shrinks, it alters (augments) density, not angular momentum, running through a one-parameter sequence of equilibrium figures. Remarkably, this same sequence is followed by a non-compressible liquid body as it enhances its momentum. According to Poincare, this body is secularly stable till it is a low-flattening Maclaurin spheroid. But when some critical eccentricity (momentum) is reached, it looses stability, takes another sequence of stable equilibrium figures - Jacobi ellipsoids - and then follows it at speedier rotations. Back.
10 "Now it is obvious
from the scheme as Hubble described it that he had an impression or a
belief, although he never quite admitted it, that it represented a
continuous sequence. But I believe, on the contrary, that Lindblad put his
finger on the essence of Hubble's classification when he suggested that it
is a series of increasing flattening, or increasing angular momentum"
(Baade 1963, p.16-17).
"According to Lindblad's theory, the fully
resolved spiral pattern is regarded as an advanced state which all nebulae
will eventually reach in the course of their evolution"
(Chandrasekhar 1942,
p.180).
Back.
11 The trend of this philosophy is sensed through the following reflection by Weizsacker (1951, p.165): "The evolution of a single object can be understood only if its temporal and spatial boundary conditions and the external forces acting on it are known. These are defined by the evolution of the larger system of which the object forms a part. So every single problem is likely to lead us back into the problem of the history of the universe". Back.
12 Circular orbits at the spheroidal edge are unstable for eccentricities e1> 0.834, and as the level e2 = 0.953 is achieved (3.1:1 axis ratio), dynamical instability against the two-crest harmonic sectorial waves is thrown in, so that the figure gets oval. Back.
13 "The most important modes of density variation" appear to be of the type of ~ (r / R)m cos(t - m) ( and m being wave frequency and azimuthal wavenumber, R - the lens radius). "The conditions for instability have been investigated for the waves m = 1, 2, 3. The greatest interest attaches to the wave m = 2 because it tends to explain the formation of barred spirals. The density variation is accompanied by the development of four whorl motions. [...] The disturbances due to the four whorls on the motions in a surrounding ring structure [the latter thought of as having been formed previously] explain in a qualitative way the development of spiral structure" (Lindblad 1962, p.147). Back.
14 These articles provide a reasonable summary of Lindblad's theories prior to 1955. The asymptotic-spiral theory was thoroughly reviewed by Chandrasekhar (1942), and the wave-mode theory by Zonn & Rudnicki (1957). See also (Lindblad 1962; Contopoulos 1972; Toomre 1977, 1996; Pasha 2000). Back.
15 In Lindblad's bar-mode theory as it had progressed by the early 1950s (Lindblad & Langebartel 1953), three factors serve for the spiral formation. The first is the tendency for the formation of the rings, one at the galaxy center and one (or several) more in the distance, the bar occupying the inter-ring region. The second factor is the development of two diametrically opposed zones of enhanced density (see Fig.2). The third one is the increased centrifugal (radial) motion in these zones. If the bar-forming processes affect the galaxy kinematics but weakly, then the motions of distant material lag behind that of the main galactic body, and as the existing radial motions make the outer ring deform and break up, it forms the main spiral arms (I and II in Fig.3). Also, the effects of the bar wave show that material at the bar `tips' has some extra rotation, so that, helped by the radial motions, it forms the inner spiral arms (VI in Fig.3). If the galactic angular momentum is above some certain level, the density wave can give no bar, and the deviations from axial symmetry it causes produce the appearance of ordinary spiral structure. Back.
16 "I remember very vividly the atmosphere in the 50's in stellar dynamics. On the one hand, we had the most general solutions of Liouville's equation by Chandrasekhar. But it was realized that the self-consistent problem required also the solution of Poisson's equation, which was very difficult in general. Thus people were discouraged." (Contopoulos) Back.
17 See, e.g., the "Critical review of cosmogonical theories prevailing in West Europe and America" by Schatzman (1954). It would be some fuller with an addendum on a theory developed in 1955-56, now in the Soviet Union, by Ogorodnikov. Finding that the works by Lindblad and Chandrasekhar on collisionless dynamics "really bar the way to studying the laws of evolution of stellar systems", he suggested a "more promising" - "synthetic" - hydrodynamical method with elements of statistical mechanics (Ogorodnikov 1958, p.20, 22), and with this he proved theorems on uniform rotation and nearly constant density for "dynamically determinable" systems, at their "most probable phase distribution". This enabled Ogorodnikov to start his supposed evolutionary sequence with the `needle-shaped' galaxies, or strongly elongated ellipsoids in rotation about their shortest axis. Such needles are secularly unstable, above all at their long-axis extremities from where "the stars are detached in two winding arms" giving the picture of a typical barred spiral galaxy. Material released during this gradual bar destruction feeds a spherical halo, while inside the bar a violent process of low-velocity-dispersion star formation starts, and these emerging Population I stars uniformly fill the new equilibrium figure - a thin disk-like Maclaurin spheroid. The remaining diffuse material of the bar (needle) winds up and, being still `frozen' in the disk, forms spiral arms. Due to irregular forces, Population I and II stars get mixed, because of which the spiral galaxy cannot be in equilibrium: its disk dies out through dissipation, and a nuclear remainder drives up an eventual elliptical galaxy (Ogorodnikov 1958, p.29).
As well illustrative appears Weizsacker's theory of galaxies and stars built on a concept of supersonic turbulent motion in the original gaseous mass, the one picturing a general "evolutionary trend as far as it does not depend on the special conditions by which galaxies, intragalactic clouds, stars, planets, etc., are distinguished". The theorist understands the rapid flattening of that gaseous mass (in about one period of rotation) as due to the decay of its original turbulence, and he reduces its further evolution to some secular changes followed by a slow loss of the axial rotation of the galactic systems. In this way, galaxies of the type of the Magellanic Clouds or the M31 companions are to be obviously younger than the universe, and "elliptic galaxies are in a final stage which no longer shows the sort of evolution we consider". "Thus the large galaxies like our own can be as old as the universe, without having yet reached their final stage", the spiral structure being their "most conspicuous semiregular pattern". Weizsacker's judgment on it is twofold. He finds himself in a position to "try to understand spiral structure as a hydrodynamical effect [...] produced by nonuniform rotation", noticing that any local formation - "cloud formed by the turbulence" - will then be distorted into a segment of a spiral. On the other hand, he admits that "the abundance of systems with just two spiral arms is probably caused not by turbulence but by gravitation", which is in fair correlation with the presence of a bar. The bar is understood as an elongated equilibrium figure of rotation similar to Jacobi's liquid ellipsoids; it "can be kinematically stable only if the system rotates uniformly", i.e. in inner galactic regions. But just a little way out, the shearing effect of differential rotation comes into play, in order "not to destroy the `bar' entirely but to distort it strongly", giving it some spiral contours (Weizsacker 1951, p.176-179). Back.
18 Zwicky reflected on the `cooperative' effects in gravitating systems (both in stars and galaxy clusters) since the mid-1930s, and he believed that whereas the nuclei of spiral galaxies had already reached their equilibrium the spiral arms and interarm regions were still "transitory configurations" (Zwicky 1957, p.214). He thus did not treat the spiral structure from the natural, for collective phenomena, viewpoint of oscillations and waves in equilibrium media. Back.
19 "Why do the spirals always show the combination of a disk and a central spheroidal system? It must reflect the original density distribution in gas. [...] Can we imagine that at some era in the past, the central spheroidal system of low rotation and the disk with very fast rotation actually resembled the equilibrium figure of the gas? One should really look into these things" (Baade 1963, p.17).
"The origin of the spiral systems is an unsolved problem as yet. Doubtless the interstellar material plays a major part in it. Therefore the methods [of stellar dynamics ... ] seem to be insufficient for a solution" (Kurth 1957, p.146). Back.
20 This was inferred from the lack of reddening of globular clusters in M31, one half of which lie behind the galaxy disk because of their spherical distribution. As Baade wrote (1963, p.70), initially one did not believe in this finding, since the gas layer in our own Galaxy was still held to be uniform. Back.
21 Baade has usually been quoted from his posthumous monograph (Baade 1963). It reproduces his 1958 lectures that vividly transmit the mid-century atmosphere in extragalactic astronomy. Many investigators of the time claimed to have agreed with Baade on the basic role of gas in the spiral arrangement (e.g., Weizsacker 1951, p.178). Back.
22 In 1958 this map was completed with the spiral fragments observed from Australia (Oort et al 1958). Back.
23 They were inferred in 1951 from data on the distribution of O-B associations and HII regions (Morgan et al 1952; see Gingerich 1985). Back.
24 Via such shifts of opinion, Lindblad found himself on the way towards "a more definite theory" (Lindblad 1962b, p.148). There he might well be judged (Toomre 1977, p.439) as if even having finally conceded that his old leading-arm models were "not reconcilable with modern evidence" (Lindblad 1962b, p.146). Yet he blamed that on some other "early gravitational theories which interpret spiral structure as due to orbital motions of stars starting from a small nucleus" (Lindblad 1962b, p.146). Back.
25 Having completed by the 1930s his theory of asymptotic leading spirals, Lindblad (1934) turned to the empirical component of the problem of the `sense of rotation' of spiral arms. The difficulty was with determining the near and the far sides of a galaxy, as this might be made no other than by way of speculation on the asymmetry of dust absorption along the minor axis of the visible image. There were at the time no reliable data on interstellar dust properties. To Lindblad's way of thinking, a stronger absorption was felt by a farther side (thought also to show sprinkles of dust veins in the bulge region), which maintained leading arms. After a categorical objection by Hubble (1943), he scrutinized the subject anew in his fundamental work with Brahde (Lindblad & Brahde 1946) followed by a succession of smaller articles during a decade or so. To criticize Lindblad for his leading-arm orientation was a commonplace. One agreed with him (and, evidently, with Hubble) in that the sense of spiral winding must be the same for all galaxies, which demanded only one good example of a nearly edge-on galaxy that might be clearly judged on both its spiral form and nearer side. de Vaucouleurs (1958) gave such an example as got a high-quality long-exposure photograph of NGC 7331 taken with the 200-inch reflector. It favored Hubble's camp. Lindblad must have reserved objections on how the spiral form was to be inferred from that crucial case (he and his collaborators Elvius and Jensen had been studying this galaxy photometrically in several papers from 1941 to 1959, and he gave a rather incomplete summary on the topic in Lindblad 1962a), but for the absolute majority of astronomers the empirical component of the sense-of-winding problem was no longer acute. Back.
26 "I cannot agree that plasma physics methods penetrated in astronomy in the 50's. Of course these developments helped each other, mainly in the 60's, but this is natural. I think that in the 50's progress was sporadic, due to the insight of only a few people, but later many people followed the first pioneers". (Contopoulos) Back.
27 Particularly, this was the line in which the unified theory of ellipsoidal equilibrium figures was being developed later (Chandrasekhar 1969). "There was criticism by astronomers of Chandrasekhar's work on the classical ellipsoids because of its remoteness from the current needs of astronomy. Chandra's interest (and my own as well) was indeed motivated by non-astronomical considerations. What we found was a development by some of the great mathematicians of the 19th and early 20th century that had largely been forgotten, and in some mathematical respects was left incomplete. Chandra felt strongly that his work should, on general intellectual grounds, be completed. If that completion should have application in astronomy, so much the better, but that was not the motivation. His critics in astronomy were offended because he was not doing astronomy. Chandra, however, was more devoted to science (or his view of it) than to astronomy, and did not feel obligated to work on problems which were chosen for him by astronomers". (Lebovitz) Back.
28 "I do remember that at the time I wrote the paper, the spiral structure of the galaxies was not even remotely in my mind. Besides my paper was concerned with the Jeans instability of a gaseous medium and not to a system of stars...However, I am quite willing to believe that the basic ideas were included in earlier papers by Lindblad". (Chandrasekhar) Back.
29 Ledoux (1951), interested in the formation of planets from a primordial cloud, seems to have been the first to consider the stability of flat gravitating systems. He, as well as Kuiper who had turned him to this problem, suspected a change in the critical Jeans scale, realizing that an assumed cloud mass of about 10% that of the Sun would be enough for the cloud to act significantly on itself in the plane of symmetry. Ledoux found that for small adiabatic disturbances to the equilibrium state of an isothermal non-rotating layer Jeans' criterion remains unaltered if is taken to be half the density value at z = 0. This did give only a correction to the clumping scale, which was of order 2 times the thickness. Fricke (1954) combined the efforts by Ledoux (1951) and Chandrasekhar (1953), yet he too could not escape certain arbitrary assumptions. And Bel & Schatzman (1958), having returned to Chandrasekhar's model, let it rotate differentially - in violation of the equilibrium conditions, though. Back.
30 Vlasov, a renowned plasma physicist, contributed to galaxy dynamics as well, via his article (Vlasov 1959) that had a special section "Spiral structure as a problem of the mathematical theory of branching of solutions of nonlinear problems". Through the collisionless Boltzmann and Poisson equations, he examined the equilibrium of an immovable plane-parallel slab, re-derived its density profile (z) ~ sech2(z / h), and `disturbed' eigenvalues of the equilibrium solution, wishing to establish the character of "infinitely close figures of equilibrium". His new solutions turned out "ribbed", or spatially periodic, with the "exfoliation period" being close to 3 kpc and corresponding to the scale of "stellar condensations observed by Oort". Despite some technical flaws (e.g., his basically smooth function (z) played as stepped one in integrations), Vlasov's conclusion about possible "ribbed" static equilibria in the tested slab was formally correct. Still, surprisingly (at least in retrospect), he gave no stability discussion, already practicable in contemporary plasma physics and very fitting as it would be for his galactic model. Back.
31 "This is in contradiction to Jeans' result, but is obtained by using his method correctly and following the consequences" (Lynden-Bell 1960a, p.204). Back.
32 Lindblad's dispersion relation in its simplest form (Lindblad 1938) was rather similar to Safronov's relation (3), both showed the same terms, but, as Lindblad was focused on global modes and Safronov dealt with short-wave radial oscillations only, their treatment of the correcting factor in gravity term was technically different. Still, "Lindblad, despite all his words, never quite seemed to relate those formulas to any spiral structures, and [...] only applied them literally to non-spiral or bar-like disturbances". (Toomre) Back.
33 Maxwell's problem was on disturbances of N equal-mass particles placed at the vertices of an N-sided regular polygon and rotating in equilibrium around a fixed central body. Back.
34 "I was delighted to see them [P.O. Lindblad's results] as evidence as to how much one could do already then (!) by way of interesting numerical studies with some hundreds of particles - in that sense his work was very inspiring. Yet [...] it also struck me that his study really dealt with not much more than the transient breakup of inherently unstable configurations of some 4 or 5 artificially introduced rings of material" that imitated "a revolving disk - one which [...] should be fiercely unstable if begun just as cold. [...] But, again, as a sample of what could already be done, P.O. Lindblad's work was indeed like a breath of fresh air". (Toomre) Back.
35 Lebedinski was another one who in his cosmogony of galaxies and stars admitted - still earlier - "the dynamical possibility of the formation of quasi-stable spiral arms rotating with a constant angular velocity for all the spiral" (Lebedinski 1954, p.30). Yet since Jeans' 1920s that idea, as such, did not sound as a novel dynamical motive. It got a really new sounding only when the fact of global galactic shearing was finally conceived. Back.
36 "It has not been possible to do justice to all phases of Lindblad's researches", Chandrasekhar `complained' already in 1942, but nonetheless he gave a "more or less complete bibliography" including 25 Lindblad's writings on the spiral problem (Chandrasekhar 1942). "The flow of his publications can be understood if one realizes that he thought in the form of a paper. When attacking a problem he started writing the paper at once". (P.O. Lindblad) Back.
<< Introduction | Contents | 2. On a New Wave Crest >>
|
Публикации с ключевыми словами:
история астрономии - спиральная галактика - волны плотности - спиральная структура
Публикации со словами: история астрономии - спиральная галактика - волны плотности - спиральная структура | |
См. также:
Все публикации на ту же тему >> | |