Мировые постоянные и предельный переход
3.09.2002 19:20 | Г. А. Гамов, Д. Д. Иваненко, Л. Д. Ландау
Мировые постоянные и предельный переход
Г.Гамов, Д.Иваненко, Л.Ландау
|
Опубликовано в "Журнале Русского физико-химического общества. Часть. физическая", т.LX, с.13, 1928. Перепечатано в журнале "Ядерная физика", 2002, т.65, сc.1406-1408, 2002, с предисловием Л.Б.Окуня, "Ядерная физика", 2002, т.65, сc.1404-1405, 2002. Сохранена орфография оригинала. |
![]() 1. При построении системы единиц в физике можно
отметить два метода выбора единиц для какой-либо новой величины:
1. При построении системы единиц в физике можно
отметить два метода выбора единиц для какой-либо новой величины:
I. Просто задается произвольный эталон (например: обычные определения грамма, ома и т.п.).
II. Пользуясь каким-либо законом A, связывающим нашу величину с уже известными и содержащими численный коэффициент, подбираем наш эталон таким образом, чтобы коэффициент обратился в единицу (например: определение единицы заряда по закону Кулона).
Всегда, конечно (отвлекаясь от технических трудностей), можно пользоваться любым из двух методов1). В первом случае мы получаем новый произвольный эталон, т.е. увеличиваем число единиц, лежащих в основе теории размерностей. Кроме того, при данном выборе эталона, коэффициент в законе A приобретает какое-то численное значение; мы получаем новую мировую постоянную.
Во втором случае как число основных произвольных эталонов, так и число мировых констант остается неизменным: мы получаем лишь естественную (по отношению к предыдущим) единицу для измерения нашей величины. Единица эта будет меняться при изменении основных эталонов. Характером этого изменения занимается дименсиональный анализ, вводящий понятнее размерности данной физической величин.
Константы нулевой размерности не зависят от выбора основных единиц и поэтому могут быть рассматриваемы как константы математические (числа). Можно надеяться, что осе эти уже числовые константы будут получены теоретически. Поэтому в рамках данной системы размерностей мировые константы, из которых можно составить агрегат нулевой размерности, должны находиться в математическом соотношении и не являются независимыми.
Из вышеизложенного следует, что мы всегда можем уменьшить число основных эталонов (число размерностей), воспользовавшись для этого одной из мировых постоянных и положив ее равной единице. (Переход от первого определения единицы ко второму.) Назовем этот процесс редукцией. Для возможности полной редукции (доведение числа эталонов до нуля) необходимо наличие независимых констант в числе не меньшем, чем число измерении, положенное в основу нашей системы единиц. Число независимых констант, очевидно, не может превысить числа независимых единиц, положенных в основу системы размерностей. Так, например: в ньютоновой механике возможна была лишь редукция к двум единицам, так как при наличии трех основных размерностей T, L, М имелся лишь один закон с мировой постоянной:
Вторая постоянная, дающая возможность редукции к одной единице, вводится частной теорией относительности соотношением:
Наконец последняя недостающая константа h фигурирует в обосновании волновой механики:
(выражение фазы ![]() через действие W).
через действие W).
Обычно мы имеем случай, когда констант (известных нам из опыта и пока еще не приведенных к меньшему числу установлением математических соотношений) гораздо больше, чем принятых нами основных единиц. В этом случае при выборе констант для совершения полной редукции выгодно выбирать константы наиболее общие.
В современной экспериментальной физике принята четверичная система
CGS1o. Техника же (из практических соображений) пользуется гораздо
большим числом узаконенных эталонов (см, г, сек, 1o, ом,
амп, ... ); здесь имеет место некая
CGS1o![]() -система.
-система.
Как на другие примеры выбора основной системы укажем на планкову
натуральную систему единиц (с, ![]() , h,
k).
, h,
k).
![]() 2. Мы видели выше, что всякая постоянная есть
представительница физического закона (теории) и как мировая
постоянная-символ его общности. Более общим законам (теориям)
соответствуют более универсальные постоянные (сравните постоянную
Ридберга с константой Планка h). Введение новых постоянных и
редукция к меньшему числу отобразились в истории физики как смена
теорий и их постепенное объединение2).
(Введение постоянной g, редукция постоянной Ридберга). По
предыдущему закрепив число измерений, мы ограничиваем и число
"истинных" постоянных: из числа имеющихся мы выбираем n констант
(n равно числу размерностей) за основные, а остальные редуцируем
к "истинным" (т.е. независимым) основным. Очевидно, безразлично, какие
постоянные принять за основные с точки зрения редукции. Здесь, однако,
мы можем руководствоваться двумя эвристическими положениями. Первое из
них - это степень общности "представляемой" теории: естественно
приводить постоянную Ридберга к планковой, а не наоборот, так как
очевидно, что теория спектров есть закономерность низшего порядка
относительно общей теории атома. Другое положение есть проба постоянной
на предельный переход, о чем речь ниже. Проследим, для примера,
биографию постоянной
h (т.е. развитие квантовой теории с точки зрения введения
постоянной). Начальной стадией можно считать классическую механику и
электродинамику. Теория Бора, старая квантовая механика вводила
h, как эмпирическую постоянную, в свои уравнения с
ограничительными целями, h - символ прерывности, скачков и т.д.
Лишь волновая механика Шредингера-Гейзенберга включает
h совершенно естественно, как постоянную размерности. Никаких
требований прерывности не вводится и эмпирическое значение h
выясняется лишь a posteriori. Мы склонны считать теорию
постоянной h законченной. Представим себе законченную (!)
физику. Построим ее на основании та размерностей; в ней, очевидно,
останется n мировых постоянных, входящих естественно, т.е. не
как эмпирические, а как простые коэффициенты размерности. Все излишние
константы будут редуцированы. Наши же мировые постоянные мы сможем
положить равными единице, по предложению Планка, т.е. перейти к физике
без размерностей. Построим систему физики, находящейся к "законченной"
в предельном отношении. Для этого применим метод предельного перехода -
будем стремить нашу постоянную к нулю (предварительно введя ее, ежели
ранее постоянная равнялась единице). Полученную предельным переходом
теорию будем называть классической относительно данной постоянной.
2. Мы видели выше, что всякая постоянная есть
представительница физического закона (теории) и как мировая
постоянная-символ его общности. Более общим законам (теориям)
соответствуют более универсальные постоянные (сравните постоянную
Ридберга с константой Планка h). Введение новых постоянных и
редукция к меньшему числу отобразились в истории физики как смена
теорий и их постепенное объединение2).
(Введение постоянной g, редукция постоянной Ридберга). По
предыдущему закрепив число измерений, мы ограничиваем и число
"истинных" постоянных: из числа имеющихся мы выбираем n констант
(n равно числу размерностей) за основные, а остальные редуцируем
к "истинным" (т.е. независимым) основным. Очевидно, безразлично, какие
постоянные принять за основные с точки зрения редукции. Здесь, однако,
мы можем руководствоваться двумя эвристическими положениями. Первое из
них - это степень общности "представляемой" теории: естественно
приводить постоянную Ридберга к планковой, а не наоборот, так как
очевидно, что теория спектров есть закономерность низшего порядка
относительно общей теории атома. Другое положение есть проба постоянной
на предельный переход, о чем речь ниже. Проследим, для примера,
биографию постоянной
h (т.е. развитие квантовой теории с точки зрения введения
постоянной). Начальной стадией можно считать классическую механику и
электродинамику. Теория Бора, старая квантовая механика вводила
h, как эмпирическую постоянную, в свои уравнения с
ограничительными целями, h - символ прерывности, скачков и т.д.
Лишь волновая механика Шредингера-Гейзенберга включает
h совершенно естественно, как постоянную размерности. Никаких
требований прерывности не вводится и эмпирическое значение h
выясняется лишь a posteriori. Мы склонны считать теорию
постоянной h законченной. Представим себе законченную (!)
физику. Построим ее на основании та размерностей; в ней, очевидно,
останется n мировых постоянных, входящих естественно, т.е. не
как эмпирические, а как простые коэффициенты размерности. Все излишние
константы будут редуцированы. Наши же мировые постоянные мы сможем
положить равными единице, по предложению Планка, т.е. перейти к физике
без размерностей. Построим систему физики, находящейся к "законченной"
в предельном отношении. Для этого применим метод предельного перехода -
будем стремить нашу постоянную к нулю (предварительно введя ее, ежели
ранее постоянная равнялась единице). Полученную предельным переходом
теорию будем называть классической относительно данной постоянной.
Так, обычная механика будет классической относительно h,
волновая механика законченной; теорию Бора с ее h, введенным
ad hoc, можно назвать вульгарной. Теория
относительности-законченная теория по отношению к 1/с
(1/с входит в метрику, как размерный коэффициент), предельной
будет также обычная механика и квантовая механика (нерелятивистская!).
Заметим, что на основании предельного перехода следует признать не
с, а 1/с истинной постоянной, так как она подвергается
стремлению к нулю. Вульгарными по отношению к 1/с были ряд
дорелятивистских электродинамик. Еще: геометрическая оптика есть
классическая теория относительно постоянной длины волны
(![]() ), а волновая оптика - законченная теория.
С этой точки зрения френелевскую теорию дифракции следует признать
вульгарной. Пользуясь этим методом, мы можем, вводя новые постоянные и
стремя их к нулю, строить новые классические теории. Последние могут
быть вдвойне, втройне и т.д. предельными (ранг классической теории).
Обычная механика, например, будет втройне предельной относительно
теорий-квантовой, релятивизма, гравитации (постоянных h,
1/с,
), а волновая оптика - законченная теория.
С этой точки зрения френелевскую теорию дифракции следует признать
вульгарной. Пользуясь этим методом, мы можем, вводя новые постоянные и
стремя их к нулю, строить новые классические теории. Последние могут
быть вдвойне, втройне и т.д. предельными (ранг классической теории).
Обычная механика, например, будет втройне предельной относительно
теорий-квантовой, релятивизма, гравитации (постоянных h,
1/с, ![]() ). Так как комбинация констант есть также
константа, то является вопрос об элементарных константах.
). Так как комбинация констант есть также
константа, то является вопрос об элементарных константах.
Мы видели, что нормальный ход развития теории был от предельной к
законченной через вульгарную. Построив параллельные схемы, мы заметим
пробелы-некоторые теории перескакивали через "вульгарный" период, для
других исторически не было предельного случая. Исторически мы имеем
L, М, T-систему размерности (не считая
температуры) и, значит, три истинные мировые постоянные. Согласно
изложенному выбор трех размерностей есть случайность, в высоком смысле
слова; относительно же выбора "истинных" постоянных мы можем следовать
эвристически общности теорий и предельному переходу. С обеих точек
зрения придется за "истинные" признать h, 1/с,
![]() (все три - представительницы наиболее развитых теорий
и удовлетворяют пробе на предельный переход).
(все три - представительницы наиболее развитых теорий
и удовлетворяют пробе на предельный переход).
![]() 3. Если мы положим, согласно предыдущему, в основу
теории размерностей три основные постоянные h, 1/с,
3. Если мы положим, согласно предыдущему, в основу
теории размерностей три основные постоянные h, 1/с,
![]() , то мы сможем получить "естественные единицы" для
всех других физических величин, в том числе для массы и для
электрического заряда. Полученные таким путем единицы заряда и массы не
совпадают с "элементарными" значениями этих величин, полученными из
опыта. (Заряд и массы электрона и протона.)
, то мы сможем получить "естественные единицы" для
всех других физических величин, в том числе для массы и для
электрического заряда. Полученные таким путем единицы заряда и массы не
совпадают с "элементарными" значениями этих величин, полученными из
опыта. (Заряд и массы электрона и протона.)
Да и трудно было бы ожидать совпадения, ибо массы электрона и протона различны, и было бы странно, чтобы одна из них оказалась основной.
Естественно ожидать, что обе эти массы будут лишь как-то выражаться через "естественную единицу" массы. Два значения для массы (m+, m-) могут быть связаны с тем, что уравнение, из которого они будут определяться, имеет два различных корня соответственно двум значениям заряда (+е;-е).
Не имея еще теории электрона, можно, однако, на основании теории
размерностей, вывести некоторые заключения о характере этой теории.
Найдем размерность заряда и массы, выраженную в наших основных
размерностях [h], [1/с], [![]() ].
Несложные выкладки дают:
].
Несложные выкладки дают:
![$$ [e] = \sqrt{[h]\cdot[c]\,};\qquad [m]=\sqrt{\frac{[h]\cdot[c]}{\chi]}\,}; \qquad \left[\frac{e}{m}\right]=\sqrt{[\chi]\,}; $$](http://images.astronet.ru/pubd/2002/09/13/0001179650/tex/formula8.gif)
или
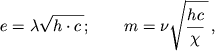
где ![]() и
и ![]() суть числовые
константы, различные для протона и
электрона. (Очевидно,
суть числовые
константы, различные для протона и
электрона. (Очевидно, ![]() )
)
Приведенные формулы размерностей могут также дать ценные указания о возможности построения теории электрона на основании неполной системы теоретической физики, когда некоторые мировые константы положены равными нулю.
Нетрудно видеть, что единственная неполная система, приводящая к конечным значениям заряда и массы, есть система:
т.е. неквантовый, нерелятивистский, гравитирующий электрон. В этом случае заряд электрона становится новой мировой постоянной.
Другие же неполные системы приводят к бесконечно малым (=большим)
зарядам или массам. В частности, обречены на неудачу часто производимые
попытки построить теорию неквантового электрона в общей теории
относительности (![]() ;
; ![]() ;
;
![]() , откуда:
, откуда: ![]() ).
).
Ленинград.
20 октября 1927 г.
1) Если имеется, конечно, закон, связывающий новую величину с раньше известными.
2) С некоторой точки зрения в каждом новом законе можно видеть новую постоянную нередуцируемую, вводя соответственную новую размерность.
|
Публикации с ключевыми словами:
фундаментальные постоянные - размерности физических величин
Публикации со словами: фундаментальные постоянные - размерности физических величин | |
|
См. также:
| |