Жесткое синхротронное излучение при аккреции вещества на одиночные черные дыры звездных масс
<< 2. Физика процессов в ... | Оглавление | 2.2. Магнитное поле >>
2.1 Темп аккреции, структура течения и унификация граничных условий
 |
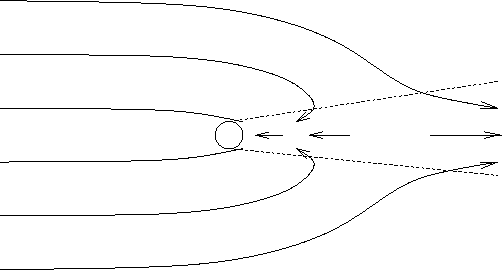Рис. 1. Крупномасштабная структура течения газа вокруг черной дыры в случае его сверхзвукового движения. Показана зона торможения позади гравитирующего центра ("хвост" черной дыры, ударная волна), а также зона сферизации вблизи него. |
Рассмотрим структуру течения вокруг движущейся в межзвездной среде черной дыры (очевидно, на больших масштабах она должна обладать цилиндрической симметрией).
Вообще говоря, задача сильно усложняется из-за бесстолкновительности среды[12] - длина свободного
пробега частиц относительно кулоновских столкновений
зачастую значительно превосходит характерный
масштаб задачи - радиус Бонди[25]
Однако задача все-таки не сводится к случаю аккреции невзаимодействующих частиц (которая была рассмотрена, например, в работах [18,28]) - ситуацию в какой-то мере спасает наличие магнитного поля[12] (роль длины свободного пробега начинает играть гораздо меньший ларморовский радиус), которое позволяет частицам обмениваться импульсом. Благодаря этому среда в некотором смысле может рассматриваться как гидродинамическая (подобная ситуация известна в физике плазмы - смотри [4]). Сразу же отметим, что наличие вмороженного магнитного поля позволяет частицам эффективно обмениваться моментом, но не энергией.
Темп аккреции на движущийся гравитирующий центр фактически определяется происходящим
вблизи оси движения позади черной дыры, где вещество теряет перпендикулярную
компоненту импульса - ее гасит вмороженное в вещество магнитное поле (или
развитие пучковых неустойчивостей после пересечения потоками частиц оси симметрии позади гравитирующего
центра[6,43], где скорость перестает быть однозначной функцией координат).
Размер этой зоны (диаметр "хвоста" черной дыры) определяется расстоянием от оси,
на котором энергия магнитного поля становится сравнимой с кинетической энергией потока, т.е.
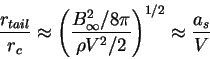
где
и 
- индукция магнитного поля и скорость звука на бесконечности, 
- скорость
движения черной дыры и учтено, что плотности тепловой и магнитной энергий межзвездной среды одного
порядка. Таким образом, диаметр "хвоста" сильно меньше характерного размера задачи - радиуса
захвата Бонди.
При дальнейшем падении на центр поток становится сферически-симметричным[12] - это видно хотя бы из несопоставимости скоростей газа на бесконечности со скоростью свободного падения вблизи нее (это подтверждается как простыми теоретическими аргументами[6,43], так и численным моделированием[41]).
При подобной структуре течения (примерный вид ее показан на рис.1) темп аккреции
не зависит от того, что именно останавливает вещество - газовое давление или магнитное поле,
а потому он определяется той же формулой, что
и в гидродинамической задаче аккреции на движущийся гравитирующий центр - формулой
Хойла-Литтлтона[39]
где
- скорость движения черной дыры, 
- концентрация частиц в межзвездной среде и
- введенный выше радиус Бонди[25].
Удобно ввести безразмерный темп аккреции как
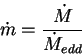
где эддингтоновский темп аккреции
Для дальнейших оценок отнормируем это выражение на массу черной дыры
масс Солнца,
концентрацию частиц 
и типичную скорость звука в межзвездной среде 
Отметим еще одно важное (и далеко не очевидное при формальном рассмотрении задачи) следствие такой структуры аккреционного потока. А именно, в зоне торможения позади черной дыры происходит перераспределение энергий аккреционного потока - вещество теряет компоненту скорости, перпендикулярную оси симметрии, по порядку величины равную скорости на бесконечности, и эта доля кинетической энергии переходит в магнитную (т.к. вещество останавливается магнитным полем), причем одновременно вещество должно нагреваться. Разумно предположить, что все три вида энергии аккреционного потока в этой зоне уравниваются, причем все они становятся порядка гравитационной энергии (условие захвата) - устанавливается равнораспределение энергий, которое, очевидно, будет сохраняться и в процессе дальнейшего падения (это значит, что отсутствуют мыслимые при формальном рассмотрении эффекты "магнитной и тепловой откачки"). Если же среда не является бесстолкновительной, то вещество в "хвосте" останавливается газовым давлением, и магнитная энергия в хвосте не приходит в равнораспределение (хотя и увеличивается по сравнению с полем на бесконечности) - в таком случае равнораспределение магнитной и гравитационной энергий устанавливается в процессе дальнейшего падения (а это происходит очень быстро при любых разумных параметрах)
Таким образом, мы можем говорить об унификации граничных условий задачи и считать, что на некотором достаточного большом радиусе поток сферически-симметричен и все виды энергии одного порядка - задача фактически сводится к случаю сферически-симметричной аккреции на покоящуюся черную дыру, где подобное равнораспределение устанавливается практически на радиусе захвата. В дальнейшем именно эту задачу мы и будем рассматривать.
<< 2. Физика процессов в ... | Оглавление | 2.2. Магнитное поле >>
|
Публикации с ключевыми словами:
конкурс - черные дыры - аккреция - Синхротронное излучение - магнитное поле
Публикации со словами: конкурс - черные дыры - аккреция - Синхротронное излучение - магнитное поле | |
См. также:
Все публикации на ту же тему >> | |
