Астронет > Колебания и волны

по текстам по ключевым словам в глоссарии по сайтам перевод по каталогу

Колебания и волны. Лекции.

В.А.Алешкевич, Л.Г.Деденко, В.А.Караваев (Физический факультет МГУ)
Издательство Физического факультета МГУ, 2001 г. Содержание

Некоторые сведения о музыкальных инструментах.

Деревянные деки музыкальных инструментов выполняют функции резонаторов, обеспечивая хорошие условия звучания. Частоты струнных инструментов не зависят от резонатора. Основная частота звука $\nu _{1}$ и частоты обертонов зависят только от массы, натяжения и длины струны. Однако тембр звука зависит от способа возбуждения и от реакции резонатора и эффективности, с которой резонатор "поддерживает" эти частоты и посылает соответствующие волны в окружающее пространство.

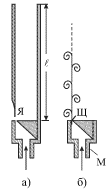
В духовых инструментах формирование звука связано с наличием автоколебаний и зависит как от конструкции инструмента, так и от способа, с помощью которого воздух вдувается в инструмент. В качестве иллюстрации рассмотрим качественно процесс возникновения автоколебаний в органной трубе, разрез которой изображен на рис. 5.17а.

Рис. 5.17.

При равномерном поступлении в мундштук М (ситуация б) воздух проходит через узкую щель Щ, за которой образуется турбулентный поток. Образующаяся при таком течении вихревая дорожка является источником "щелевого" тона, основная частота которого обратно пропорциональна периоду следования вихрей $T_{в}.$ По существу система "мундштук + щель" представляет собой сложную автоколебательную систему, теоретическое описание которой - серьезная проблема.

Вихри, выходящие из щели, поочередно проходят слева и справа от язычка Я, вызывая его вибрацию (ситуация а). Язычок оказывает периодическое воздействие на столб воздуха в трубе. Возникающие в столбе импульсы сжатия, добежав до открытого конца трубы, отражаются в виде импульсов разрежения и возвращаются к щели через время $T = 2\ell / c$ ( $\ell$ - длина трубы, $c$ - скорость звука в воздухе), управляя поступлением воздуха через щель. Таким образом, основная частота $\nu _{1} = 1 / T$ формируется резонаторной системой. Однако можно вдувать воздух так, чтобы в трубе одновременно существовали два импульса сжатия, и мы услышим звучание трубы на частоте первого обертона (удвоенной частоте).

Органные трубы обычно конструируются для звучания на основной частоте. В духовых инструментах возбуждающим вибратором (аналогом язычка Я в органной трубе) можно управлять, чтобы посылать в трубу один или более импульсов, прежде чем первый отразится от открытого конца. Высота звука инструмента определяется количеством импульсов в секунду, отраженных от открытого конца духового инструмента.

Произносимые человеком звуки связаны с тем, что голосовые связки гортани вибрируют под напором движущегося воздуха, а гортань является объемным резонатором. Как правило, у мужчин объем гортани больше, чем у женщин, поэтому в соответствии с формулой (5.34) мужские голоса более низкие.

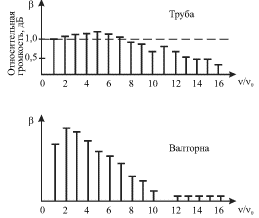
На рис. 5.18 показаны спектры звуков, извлекаемых на трубе и валторне с одинаковой основной частотой $\nu _{0} = 440 Гц.$ По оси ординат отложена громкость $\beta$ (нормирована на громкость волны основной частоты). В спектре звука валторны отсутствуют частоты $\nu \gt 10 кГц,$ поэтому её звук более приглушенный, нежели звук трубы.

Рис. 5.18.

Завершая описание основных принципов действия источников звука и музыкальных инструментов, уместно упомянуть о двух акустических эффектах, с проявлениями которых мы практически ежедневно встречаемся.

Эффект Доплера.

Наблюдая за проходящим мимо поездом или движущимся автомобилем, мы замечаем, что высота тона подаваемого ими звукового сигнала постоянно изменяется. Это и есть одно из проявлений эффекта Доплера, состоящего в изменении частоты звука при относительном движении источника и приемника. Рассмотрим это явление несколько подробнее.

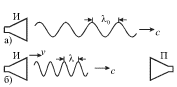
Пусть источник И (рис. 5.19а) излучает монохроматическую (т.е. гармоническую) акустическую волну частоты $\nu _{0}.$ Тогда длина этой волны, распространяющейся в воздухе со скоростью с, будет равна:

$\lambda _{0} = c / \nu _{0}.$

(5.37)

Рис. 5.19.

Если теперь источник будет двигаться со скоростью $v \lt c$ в направлении распространения волны, то волна будет "отрываться" от источника со скоростью $c - v,$ и её длина уменьшится (рис. 5.19б):

$\lambda = {\displaystyle \frac{\displaystyle {\displaystyle c - v}}{\displaystyle {\displaystyle \nu _{0} }}}.$

(5.38)

Достигнув неподвижного приемника П, эта волна будет воздействовать на него с частотой

$\nu = {\displaystyle \frac{\displaystyle {\displaystyle c}}{\displaystyle {\displaystyle \lambda }}} = \nu _{0} {\displaystyle \frac{\displaystyle {\displaystyle c}}{\displaystyle {\displaystyle c - v}}} = \nu _{0} {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 1 - v / c}}},$

(5.39)

которая будет больше исходной частоты $\nu _{0}.$ При движении источника в противоположном направлении эта частота уменьшится. Именно это изменение частоты тона сигнала мы фиксируем при приближении и последующем удалении поезда или автомобиля.

Изменение частоты будет также и при движении приемника П, однако физическая причина этого изменения состоит в том, что волна с длиной $\lambda _{0} = c / \nu _{0}$ будет поступать в приемник со скоростью $v + c$ (если приемник движется навстречу волне). Следовательно, частота воздействия на приемник будет равна

$\nu = {\displaystyle \frac{\displaystyle {\displaystyle c + v}}{\displaystyle {\displaystyle \lambda _{0} }}} = \nu _{0} {\displaystyle \frac{\displaystyle {\displaystyle c + v}}{\displaystyle {\displaystyle c}}} = \nu _{0} \left( {\displaystyle 1 + {\displaystyle \frac{\displaystyle {\displaystyle v}}{\displaystyle {\displaystyle c}}}} \right)$

(5.40)

и превысит исходную частоту.

В силу различия физических причин, приводящих к изменению частоты при движении источника и приемника, разнятся и формулы (5.39) и (5.40). Однако при $v \ll c,$ как нетрудно убедиться, с точностью до членов порядка $\left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle v}}{\displaystyle {\displaystyle c}}}} \right)^{2}$ формула (5.39) может быть записана в виде (5.40).

При одновременном движении навстречу друг другу источника со скоростью $v_{и}$ и приемника со скоростью $v_{п}$ обе формулы можно объединить в одну

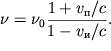$\nu = \nu _{0} {\displaystyle \frac{\displaystyle {\displaystyle 1 + v_{п} / c}}{\displaystyle {\displaystyle 1 - v_{и} / c}}}.$

(5.41)

При удалении источника или приемника в формуле (5.41) следует изменить знак при соответствующей скорости.

При скоростях $v \gt c$ формируются ударные волны, и формулы, описывающие изменение частоты, становятся несправедливыми.

Бинауральный эффект.

Этот эффект представляет собой психофизиологическое явление, заключающееся в слитном восприятии звуков, принимаемых правым и левым ухом. Он дает возможность определить направление на источник звука и играет существенную роль в музыкальной акустике (стереофония).

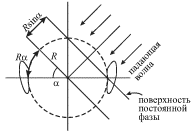
Рисунок 5.20 иллюстрирует этот эффект. Если волна падает под углом $\alpha$ к линии, соединяющей оба уха (пунктиром изображен контур радиуса $R,$ имитирующий голову человека), то волна достигнет левого уха позднее правого, а время задержки составит величину

$\Delta t = {\displaystyle \frac{\displaystyle {\displaystyle R\sin \alpha + R\alpha }}{\displaystyle {\displaystyle c}}},$

(5.42)

где $R\alpha$ - криволинейный путь, проходимый звуковой волной при огибании ею головы человека за счет дифракции (см. ниже).

Рис. 5.20.

Кроме того, поскольку голова частично экранирует звук, то амплитуда волны, достигающей левого уха, несколько уменьшается. Совместное действие этих двух факторов дает человеку возможность определить направление на источник звука. Если период колебаний звуковой волны сравним со временем задержки:

$\Delta t \le T / 2,$

(5.43)

то волны, падающие под углом, вызывают колебания барабанных перепонок левого и правого уха со сдвигом фаз $0 \le \Delta \varphi \le \pi,$ по которому человек и определяет направление прихода волны.

Если положить $R = 10 см,\; \sin \alpha \approx 1,$ то для волн с периодом $T \lt 10^{ - 3} с\; (\nu \ge 1 кГц)$ условие (5.43) не выполняется, и определить направление по сдвигу фазы становится затруднительно. Однако остается возможность сравнить амплитуды волн, достигающих обоих ушей, и тем самым определить угол $\alpha.$

Интерференция волн.

В предыдущей лекции мы получили уравнение стоячей волны (4.34), описывающее колебания шнура (или иной среды), по которому навстречу друг другу распространяются две гармонические волны одинаковой частоты $\omega$ и амплитуды $s_{0}.$ В результате наложения волн происходит перераспределение в пространстве объемной плотности энергии колебаний. В узлах, где волны встречаются в противофазе, эта энергия равна нулю. В пучностях, напротив, волны складываются в фазе, и энергия максимальна. Явление наложения волн, приводящее к перераспределению в пространстве объемной плотности энергии колебаний, носит название интерференции.

Интерференция является одним из фундаментальных явлений, присущих волнам различной природы (акустическим, электромагнитным, волнам на поверхности жидкости, плазменным волнам и др.). Она была хорошо известна еще во времена Ньютона, который осуществил замечательный опыт, приведший к открытию закономерностей интерференционной картины и получивший название "кольца Ньютона". Эти закономерности легко прослеживаются в опытах по интерференции капиллярных волн на поверхности жидкости. В следующей лекции дается описание характера движения частиц жидкости в таких волнах и устанавливается связь между частотой, длиной волны и скоростью ее распространения.

Назад| Вперед

Публикации с ключевыми словами: колебания - волны Публикации со словами: колебания - волны
См. также: Эхо из глубин красного гиганта

Обсудить эту публикацию

Версия для печати

Астрометрия - Астрономические инструменты - Астрономическое образование - Астрофизика - История астрономии - Космонавтика, исследование космоса - Любительская астрономия - Планеты и Солнечная система - Солнце