Астронет > Колебания и волны

по текстам по ключевым словам в глоссарии по сайтам перевод по каталогу

Колебания и волны. Лекции.

В.А.Алешкевич, Л.Г.Деденко, В.А.Караваев (Физический факультет МГУ)
Издательство Физического факультета МГУ, 2001 г. Содержание

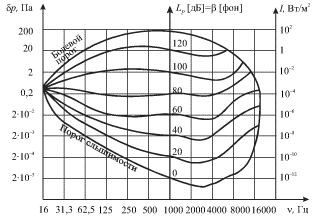
На рис. 5.12 изображена "диаграмма слуха", на которой показаны области частот и звуковых давлений, а также уровни интенсивности звуков, воспринимаемых человеческим ухом. Нормальное ухо слышит только те звуки, которые лежат внутри этой области. Нижняя граница области характеризует зависимость порога слышимости от частоты, а верхняя - порог болевого ощущения, когда волна перестает восприниматься как звук, вызывая в ухе ощущение боли и давления. Отметим, что человеческое ухо является уникальным приемником акустических волн, воспринимающим звуки, различающиеся по интенсивности на 12-15 порядков в области частот около 1 кГц, где диаграмма слуха имеет наибольшее вертикальное сечение. Из диаграммы видно, что при одинаковом звуковом давлении и одинаковой интенсивности звуки различной частоты могут восприниматься, как звуки разной громкости $\beta.$ Поэтому в акустике, помимо субъективной величины - громкости звука $\beta,$ оцениваемой на слух, используются и объективные характеристики звука, которые могут быть непосредственно измерены, - уровень звукового давления $L_{p}$ и равный ему уровень интенсивности. Поскольку согласно (5.17) интенсивность пропорциональна квадрату звукового давления, обе эти характеристики определяются формулой:

$L_{p} = 2\lg {\displaystyle \frac{\displaystyle {\displaystyle \delta p}}{\displaystyle {\displaystyle \delta p_{пор} }}} = \lg {\displaystyle \frac{\displaystyle {\displaystyle I}}{\displaystyle {\displaystyle I_{пор} }}}.$

(5.30)

Рис. 5.12.

В принципе, $L_{p}$ - величина безразмерная, но для численного значения логарифма используют название "Бел" (в честь изобретателя телефона Г. Белла). На практике обычно используют в 10 раз меньшую единицу - "децибел", так что (5.30) принимает вид:

$L_{p} [дБ] = 20\lg {\displaystyle \frac{\displaystyle {\displaystyle \delta p}}{\displaystyle {\displaystyle \delta p_{пор} }}} = 10\lg {\displaystyle \frac{\displaystyle {\displaystyle I}}{\displaystyle {\displaystyle I_{пор} }}}.$

(5.30а)

В определении $L_{p}$ принято использовать стандартный порог слышимости $\delta p_{пор} = 2 \cdot 10^{ - 5} Па,$ а соответствующее ему значение минимальной интенсивности $I_{пор}$ зависит, согласно (5.17), от среды, в которой распространяется звук, и для воздуха при нормальных условиях составляет $I_{пор} = 10^{ - 12} Вт/м^{2}.$

Для громкости звука $\beta$ используют единицу под названием "фон". Громкость тона в фонах для любой частоты равна уровню звукового давления в децибелах для тона с частотой $\nu = 1 кГц,$ воспринимаемого как звук той же громкости.

На рис. 5.12 изображены также кривые для уровней равной громкости при различных уровнях звукового давления и интенсивности, из которых видно, что при $\nu = 1 кГц\; \beta = L_{p},$ а для других слышимых ухом частот $\beta$ и $L_{p}$ могут заметно отличаться.

Акустические резонаторы.

В ряде случаев возникает необходимость выделения гармонических составляющих из сложных звуковых колебаний. С такой задачей приходится сталкиваться при упомянутом выше спектральном анализе сложных звуков, при создании узкополосных приемников звука, чувствительных к определенной частоте, музыкальных инструментов и др. Для таких целей используется акустический резонатор - устройство, обладающее одной или множеством собственных частот.

Типичным примером акустической системы, реагирующей лишь на одну частоту, является сосуд сферической формы с открытой горловиной (рис. 5.13), который называется резонатором Гельмгольца. В задней части резонатора имеется еще одно маленькое отверстие в виде сопла, служащее для обнаружения колебаний. Воздух в горловине является колеблющейся массой. При смещении этой массы, например, в сторону сферического объема $V$ воздух в этом объеме слегка сжимается, и возникающие силы избыточного давления выполняют роль возвращающей силы. Если площадь горловины равна $S,$ а её длина - $\ell,$ то масса колеблющегося столба равна $m = \rho _{0} \ell S,$ где $\rho _{0}$ - плотность невозмущенного воздуха. При смещении массы $m$ на расстояние $\xi \ll \ell$ (положительное направление оси $O\xi$ показано на рисунке) плотность воздуха изменяется на величину $\delta \rho,$ удовлетворяющую равенству

${\displaystyle \frac{\displaystyle {\displaystyle \delta \rho }}{\displaystyle {\displaystyle \rho _{0} }}} = - {\displaystyle \frac{\displaystyle {\displaystyle S \cdot \xi }}{\displaystyle {\displaystyle V}}}.$

(5.31)

Согласно (5.7), избыточное давление оказывается равным

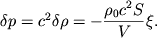$\delta p = c^{2}\delta \rho = - {\displaystyle \frac{\displaystyle {\displaystyle \rho _{0} c^{2}S}}{\displaystyle {\displaystyle V}}}\xi.$

(5.32)

Следовательно, уравнение движения столба воздуха принимает вид

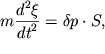$m{\displaystyle \frac{\displaystyle {\displaystyle d^{2}\xi }}{\displaystyle {\displaystyle dt^{2}}}} = \delta p \cdot S,$

или

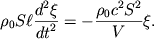$\rho _{0} S\ell {\displaystyle \frac{\displaystyle {\displaystyle d^{2}\xi }}{\displaystyle {\displaystyle dt^{2}}}} = - {\displaystyle \frac{\displaystyle {\displaystyle \rho _{0} c^{2}S^{2}}}{\displaystyle {\displaystyle V}}}\xi.$

(5.33)

Отсюда находим, что собственная частота колебаний столба воздуха в горловине, или частота резонатора Гельмгольца, равна

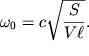$\omega _{0} = c\sqrt {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle S}}{\displaystyle {\displaystyle V\ell }}}}.$

(5.34)

При объеме резонатора $V = 10^{ - 3} м^{3},$ площади отверстия горловины $S = 1 см^{2}$ и её длине $\ell = 1 см,$ скорости звука $c = 334 м/с$ для частоты $\nu _{0}$ получим величину

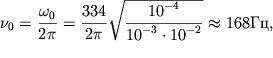$\nu _{0} = {\displaystyle \frac{\displaystyle {\displaystyle \omega _{0} }}{\displaystyle {\displaystyle 2\pi }}} = {\displaystyle \frac{\displaystyle {\displaystyle 334}}{\displaystyle {\displaystyle 2\pi }}}\sqrt {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle 10^{ - 4}}}{\displaystyle {\displaystyle 10^{ - 3} \cdot 10^{ - 2}}}}} \approx 168 Гц,$

(5.35)

соответствующую слышимому диапазону звуковых частот.

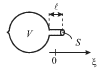Рис. 5.13.

Зависимость собственной частоты колебаний резонатора от его параметров и прежде всего от объема $V$ эффектно демонстрируется в следующем опыте (рис. 5.14). Перед динамиком Д, подключенным к генератору звуковой частоты Г устанавливаются несколько резонаторов, отличающихся своими размерами. Около заднего отверстия каждого из резонаторов помещается легкий бумажный пропеллер-вертушка, который может вращаться вокруг вертикальной оси. При плавном увеличении частоты звукового генератора будет возрастать частота акустической волны, испускаемой динамиком в направлении резонаторов и играющей роль гармонической вынуждающей силы. При последовательном совпадении частоты этой волны $\nu$ с собственными частотами $\nu _{1}, \nu _{2}$ и $\nu _{3}$ резонаторов давление воздуха в их объемах будет колебаться с максимальной (резонансной) амплитудой. Из задних отверстий резонаторов будут бить сильные струи воздуха, что фиксируется по началу вращения вертушек сначала у большого, затем у среднего и, наконец, у самого маленького резонатора, имеющего самую высокую собственную частоту $\nu _{3} .$

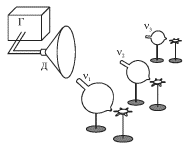Рис. 5.14.

Уместно отметить, что при частоте резонатора $\nu _{0} \sim 10^{2} Гц$ длина возбуждающей его волны $\lambda = c / \nu _{0} \approx 3,3 м.$ Эта длина значительно больше характерных размеров резонатора: $\lambda \gg V^{1 / 3}.$ Следовательно, не может быть и речи о стоячей акустической волне частоты $\nu _{0}$ в самой сферической полости.

Однако и в самой полости можно возбудить стоячие волны с длиной $\lambda \le V^{1 / 3}$ и частотой $\nu = c / \lambda \ge c / V^{1 / 3}.$ Если характерный размер резонатора $V^{1 / 3}\sim 10 см,$ то частоты этих волн $\nu \gt 3000 Гц.$ Такой резонатор будет обладать множеством собственных частот в килогерцовом диапазоне.

Наиболее простым в изготовлении акустическим резонатором является деревянный ящик или труба, открытые либо с одной, либо с двух противоположных сторон.

Проделаем следующий опыт. Заполним водой нижнюю часть вертикальной трубки Т, используя систему сообщающихся сосудов, и поднесем к верхнему концу звучащий на частоте $\nu$ камертон К (рис. 5.15). Перемещая воронку В вверх, можно добиться усиления тонального звука, создаваемого системой "камертон + часть трубы, заполненная воздухом". Это усиление будет при совпадении частоты $\nu$ с одной из собственных частот $\nu _{p}$ резонатора - трубы с воздухом длиной $\ell,$ "закрытой" у нижнего конца. Собственные частоты стоячих волн в таком резонаторе легко подсчитать, если учесть, что на нижнем конце должен быть узел смещений, а на верхнем - пучность. Это возможно лишь для длин волн $\lambda _{p},$ удовлетворяющих изложенному в предыдущей лекции условию (4.40):

$\ell = (2p - 1){\displaystyle \frac{\displaystyle {\displaystyle \lambda _{p} }}{\displaystyle {\displaystyle 4}}}, p = I, II, III, \ldots ,$

когда на длине трубы укладывается нечетное число четвертей длин волн. Соответственно, частоты колебаний будут равны

$\nu _{p} = {\displaystyle \frac{\displaystyle {\displaystyle c}}{\displaystyle {\displaystyle \lambda _{p} }}} = {\displaystyle \frac{\displaystyle {\displaystyle c}}{\displaystyle {\displaystyle 4\ell }}}(2p - 1).$

(5.36)

Хотя усиление звука будет при нескольких длинах воздушного столба $\ell,$ однако самым эффективным оно будет при $\nu = \nu _{I}$ или $\ell = {\displaystyle \frac{\displaystyle {\displaystyle c}}{\displaystyle {\displaystyle 4\nu }}}.$

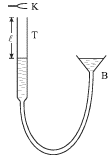Рис. 5.15.

Особо подчеркнем, что резонатор создает более благоприятные условия для звучания камертона, позволяя перераспределить, а стало быть и усилить звук по определенным направлениям. Именно поэтому в опытах камертоны устанавливают на деревянный ящик, открытый с одного конца и настроенный на частоту камертона (рис. 5.16).

Рис. 5-16.

Назад| Вперед

Публикации с ключевыми словами: колебания - волны Публикации со словами: колебания - волны
См. также: Эхо из глубин красного гиганта

Обсудить эту публикацию

Версия для печати

Астрометрия - Астрономические инструменты - Астрономическое образование - Астрофизика - История астрономии - Космонавтика, исследование космоса - Любительская астрономия - Планеты и Солнечная система - Солнце