Астронет > Колебания и волны

по текстам по ключевым словам в глоссарии по сайтам перевод по каталогу

Колебания и волны. Лекции.

В.А.Алешкевич, Л.Г.Деденко, В.А.Караваев (Физический факультет МГУ)
Издательство Физического факультета МГУ, 2001 г. Содержание

Баллистический режим колебаний.

Рассмотрим колебания системы, к которой приложена произвольная сила $F(t),$ действующая в течение промежутка времени $\Delta t,$ значительно меньшего периода собственных колебаний: $\Delta t \ll T.$ Отклик системы на такое воздействие будет пропорционален импульсу действующей силы:

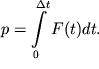$p = {\displaystyle \int\limits_{0}^{\Delta t} {\displaystyle F(t)dt.} }$

(2.42)

В самом деле, при кратковременном воздействии (в течение времени $\Delta t)$ маятник не успевает заметно сместиться из положения равновесия, однако будет обладать ускорением

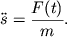$\ddot {\displaystyle s} = {\displaystyle \frac{\displaystyle {\displaystyle F(t)}}{\displaystyle {\displaystyle m}}}.$

(2.43)

При записи (2.43) мы пренебрегли силой вязкого трения. По окончании действия силы маятник приобретет скорость

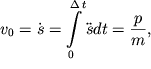$v_{0} = \dot {\displaystyle s} = {\displaystyle \int\limits_{0}^{\Delta \,t} {\displaystyle \ddot {\displaystyle s}dt} } = {\displaystyle \frac{\displaystyle {\displaystyle p}}{\displaystyle {\displaystyle m}}},$

(2.44)

пропорциональную импульсу силы.

Далее маятник будет совершать собственные гармонические колебания с амплитудой

$s_{0} = {\displaystyle \frac{\displaystyle {\displaystyle v_{0} }}{\displaystyle {\displaystyle \omega _{0} }}} = {\displaystyle \frac{\displaystyle {\displaystyle p}}{\displaystyle {\displaystyle m\omega _{0} }}}.$

(2.45)

Если параметры $m$ и $\omega _{0}$ известны, то измеряя амплитуду первого колебания после воздействия, можно определить $p.$

В качестве примера рассмотрим процедуру измерения заряда, протекающего по электрической цепи, с использованием баллистического гальванометра. Этот гальванометр содержит рамку, которая может совершать крутильные колебания. Рамка имеет увеличенный (по сравнению с обычным гальванометром) момент инерции, что увеличивает период ее собственных колебаний до нескольких секунд. Т.к. рамка находится в магнитном поле постоянного магнита, то при протекании через нее электрического тока на рамку будет действовать момент сил, пропорциональный току. При протекании кратковременного тока рамка приобретает угловую скорость и затем за четверть периода колебаний отклоняется на некоторый максимальный угол, который пропорционален интегралу от протекшего через рамку тока, т.е. величине протекшего заряда.

Установление колебаний.

Мы уже отмечали, что если приложить к покоящемуся маятнику гармоническую силу в момент времени $t = 0,$ то маятник начнет постепенно раскачиваться, как это качественно изображено на рис. 2.7а. Установление колебаний связано с тем фактом, что наряду с вынужденными колебаниями на частоте $\omega$ будут возбуждены и собственные колебания на частоте $\sqrt {\displaystyle \omega _{0}^{2} - \delta ^{2}},$ которые, конечно, будут затухать.

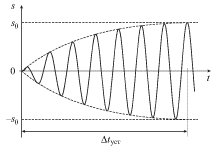Рис. 2.7а.

Из математики известно, что общее решение линейного неоднородного уравнения (2.10) при $\delta \lt \omega _{0}$ имеет вид:

$s(t) = s_{0c} e^{ - \delta t}\sin (\sqrt {\displaystyle \omega _{0}^{2} - \delta ^{2}} t + \varphi _{c} ) + s_{0} \sin (\omega t + \varphi _{0} ),$

(2.50)

представляющий собой суперпозицию собственных затухающих колебаний на частоте $\sqrt {\displaystyle \omega _{0}^{2} - \delta ^{2}}$ и незатухающих вынужденных колебаний на частоте $\omega .$ Из (2.50) видно, что колебания установятся лишь тогда, когда затухнут собственные колебания. Это произойдет по истечении времени

$\Delta t_{уст} \sim \tau = {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle \delta }}}.$

(2.51)

За это время в систему "закачивается" энергия, поскольку до установления колебаний работа внешней силы превышает работу сил трения. В установившемся режиме имеет место баланс поступающей и расходуемой энергий.

В частности, если $\omega = \sqrt {\displaystyle \omega _{0}^{2} - \delta ^{2}} ,$ то (2.50) при $s(0) = 0, \dot {\displaystyle s}(0) = 0$ и $\delta \ll \omega _{0} ,$ как нетрудно показать, имеет вид

$s(t) = s_{0} (1 - e^{ - \delta t})\sin (\omega t - \pi / 2),$

(2.52)

поскольку при этих условиях $s_{0c} = s_{0} , \varphi _{c} = - \varphi _{0} \approx {\displaystyle \frac{\displaystyle {\displaystyle \pi }}{\displaystyle {\displaystyle 2}}}.$

Отметим, что формула (2.51) определяет лишь порядок величины (временной масштаб) $\Delta t_{уст} .$ Для практических целей время установления (равно как и время затухания) колебаний принимают равным $\Delta t_{уст} = (3\div 5)\tau .$

На фазовой плоскости (рис. 2.7б) фазовая траектория будет постепенно "раскручиваться" из начала координат и стремиться к предельному циклу - эллипсу, изображенному на рисунке пунктирной линией.

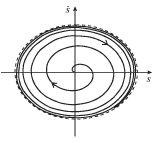Рис. 2.7б.

Характеристики различных колебательных систем (осцилляторов).

Интересно сопоставить основные характеристики различных колебательных систем (иногда их для краткости называют осцилляторами) Примерами таких осцилляторов могут быть механические (рассмотренные выше), электрические (известные из школьного курса физики, например, колебательный контур), оптические (например, электрон в атоме) и другие системы.

Вначале обратимся к характеристикам наиболее распространенного осциллятора - маятника, представляющего собой тело, подвешенное на нити.

Маятник является одним из древнейших физических приборов. С помощью крутильных маятников были открыты законы гравитационного и электрического взаимодействий, измерено давление света, выполнено множество других физических экспериментов. В последнее время предложен и реализуется ряд новых экспериментов для изучения фундаментальных свойств материи, в которых очень малые силы измеряются с помощью крутильных маятников. Чувствительность таких экспериментов зависит от того, насколько ослаблены сейсмические возмущения, действующие на маятник, а также от стабильности его параметров, например, упругих свойств нити подвеса. Но даже если устранены все внешние возмущающие воздействия, остается один принципиальный источник флуктуаций его амплитуды и фазы колебаний. Это хаотическое тепловое движение молекул в нити подвеса и подвешенном теле. Действующая на него флуктуационная сила зависит от температуры и от добротности маятника. Чем выше добротность маятника, тем медленнее затухают его колебания и диссипирует его энергия, превращаясь в тепло, т.е. хаотическое движение молекул. Это означает, что ослабевает и обратный процесс раскачки маятника хаотическим движением молекул, т.е. уменьшается флуктуационная сила, действующая на маятник. Для того, чтобы уменьшить затухание, тело и нить подвеса изготовляют из высококачественного плавленого кварца - материала с низкими потерями упругой энергии, а также принимают специальные меры для исключения других источников диссипации энергии. В результате добротность крутильных маятников достигает величины ~10⁷.

В настоящее время в нескольких странах строятся лазерные гравитационные антенны для регистрации гравитационного излучения от космических объектов. Принцип действия антенны основан на том, что гравитационная волна действует на свободные массы, помещенные в разные точки пространства, изменяя расстояние между ними. Это изменение пропорционально интенсивности волны и расстоянию между массами. По этой причине в гравитационных антеннах пробные массы располагают в нескольких километрах друг от друга в специальных вакуумных камерах, а расстояние между ними измеряют уникальным лазерным интерферометром. Каждая пробная масса подвешивается на тонких нитях, образуя маятник качания. С массами связывают два зеркала, отражающие лазерный луч, распространяющийся вдоль прямой, соединяющей эти массы. По сдвигу интерференционной картины, даваемой такой сложной оптической системой, можно "почувствовать" взаимное смещение масс на величину порядка 10^-17 см, что на 7 порядков меньше размеров атома! Чувствительность гравитационной антенны ограничена тепловыми флуктуациями колебаний такого маятника, а значит, также определяется его добротностью. В отличие от крутильных, добротность маятников качания зависит не только от потерь в упругом элементе - нити подвеса, но и от ее натяжения. За счет этого эффекта можно значительно увеличить добротность маятника качания. Так, добротность маятников качания, целиком изготовленных из плавленого кварца, может превышать 10⁸, т.е. время затухания их колебаний достигает нескольких лет. Конечно, при столь малой диссипации энергии маятника на его добротность влияют весьма слабые внешние воздействия, например, электрические и магнитные поля, или частицы пыли, осевшие на нити подвеса, и т. д.

При таких высоких значениях добротности и соответствующем подавлении сейсмических возмущений проявляются квантовые свойства маятника. В этом случае поведение вполне макроскопического объекта будет определяться принципом неопределенности Гейзенберга. Правда, необходимые условия реализуются пока для малых временных интервалов (около 10^-3 с), и для наблюдения квантовых особенностей поведения маятников требуются очень чувствительные регистрирующие устройства, но именно такие маятники, обладающие предельно высокой добротностью, предполагается использовать в будущих гравитационных антеннах.

Камертон, служащий для настройки музыкальных инструментов, также является высокодобротным осциллятором. Звук, издаваемый вибрирующими ножками камертона, затихает за достаточно длительное время по сравнению с периодом их колебаний. Если, например, собственная частота камертона лежит в диапазоне $\nu = 300\div 400 Гц,$ а продолжительность звучания (весьма грубо) составляет время порядка $\tau \sim 10 с,$ то камертон совершит $\nu \tau \sim 3000\div 4000$ колебаний. Это означает, что его добротность по порядку величины равна $Q\sim 10^{4}.$

Как это ни покажется парадоксальным, электрический колебательный контур является менее добротной системой, хотя частота его собственных колебаний имеет порядок величины $\nu \sim (10^{5}\div 10^{8}) Гц.$ Добротность контура ограничена, главным образом, омическими потерями и имеет порядок величины $Q\sim 10^{2}.$ Это, в свою очередь, означает, что полоса пропускания $\Delta \nu = Q^{ - 1} \cdot \nu ,$ введенная ранее при рассмотрении вынужденных колебаний, равна $\Delta \nu \sim (10^{3}\div 10^{6}) Гц.$

Если частота радиопередающей станции $\nu _{c}$ высока $(\nu _{c} \gt 10^{6} Гц),$ то ее преобразовывают в радиоприемных устройствах до низкой (называемой промежуточной) частоты $\nu _{п} \sim 10^{5} Гц.$ Тогда колебательный контур радиоприемника будет иметь очень малую полосу пропускания $\Delta \nu \sim Q \cdot \nu _{п} \sim 5 \cdot 10^{3} Гц.$ Это значит, что если частоты двух станций $\nu _{1c}$ и $\nu _{2c}$ соответственно различаются более, чем на величину полосы пропускания $({\displaystyle \left| {\displaystyle \nu _{1c} - \nu _{2c} } \right|} \gt \Delta \nu ),$ то, перестраивая собственную частоту колебательного контура приемника, можно по отдельности настроиться на каждую из этих передающих станций.

Оптический электрон в атоме, осуществляя переходы с одной орбиты на другую, в соответствии с постулатами Бора излучает квант света с энергией $\hbar \omega = E_{2} - E_{1} .$ С классической точки зрения это можно интерпретировать таким образом, что электрон совершает колебания на этой частоте $\omega ,$ т.е. является оптическим осциллятором. Поскольку электрон теряет энергию на излучение, то амплитуда его колебаний должна затухать в течение некоторого характерного времени $\tau .$ Для уединенного атома (не взаимодействующего с соседними атомами) это время определяется зарядом и массой электрона и зависит от частоты $\omega .$ Однако для всех атомов оно имеет один и тот же порядок величины: $\tau \sim 10^{ - 8}\div 10^{ - 9}c.$ Учитывая, что в видимом оптическом диапазоне период колебаний $T = {\displaystyle {\displaystyle 2\pi } / {\displaystyle \omega }}\sim 10^{ - 15}c,$ легко подсчитать число колебаний до их затухания. Оно имеет порядок величины ${\displaystyle \frac{\displaystyle {\displaystyle \tau }}{\displaystyle {\displaystyle T}}}\sim 10^{6}\div 10^{7}.$ Поэтому добротность оптического осциллятора $(Q\sim 10^{7}),$ будучи высокой, все же уступает добротности прецизионных кварцевых маятников.

Назад| Вперед

Публикации с ключевыми словами: колебания - волны Публикации со словами: колебания - волны
См. также: Эхо из глубин красного гиганта

Обсудить эту публикацию

Версия для печати

Астрометрия - Астрономические инструменты - Астрономическое образование - Астрофизика - История астрономии - Космонавтика, исследование космоса - Любительская астрономия - Планеты и Солнечная система - Солнце