Механика твердого тела. Лекции.
В.А.Алешкевич, Л.Г.Деденко, В.А.Караваев (Физический факультет МГУ)Издательство Физического факультета МГУ, 1997 г. Содержание
Проецируя векторы L и ![]() на оси системы xyz, жестко связанной с
твердым телом, получим:
на оси системы xyz, жестко связанной с
твердым телом, получим:
| (3.49) |
| (3.50) |
| (3.51) |
Поскольку оси Ox, Oy и Oz - главные оси инерции для точки закрепления, то
![]() и из (3.49-3.51) будем иметь следующие уравнения:
и из (3.49-3.51) будем иметь следующие уравнения:
| (3.52) |
| (3.53) |
| (3.54) |
где ![]() - главные моменты инерции тела. Обычно эти
уравнения называют уравнениями Эйлера при отсутствии моментов внешних сил.
- главные моменты инерции тела. Обычно эти
уравнения называют уравнениями Эйлера при отсутствии моментов внешних сил.
В частном случае (рис. 3.14) ![]() и из (3.52-3.54) получаем:
и из (3.52-3.54) получаем:
| (3.55) |
| (3.56) |
| (3.57) |
где введено обозначение
| (3.58) |
Из (3.57) следует, что ![]() то есть проекция вектора
то есть проекция вектора ![]() на ось симметрии тела остается постоянной. Ясно, что
на ось симметрии тела остается постоянной. Ясно, что ![]() - также
постоянная величина. Ее физический смысл становится понятным, если записать
решение уравнений (3.55, 3.56):
- также
постоянная величина. Ее физический смысл становится понятным, если записать
решение уравнений (3.55, 3.56):
| (3.59) |
где ![]() -
проекция вектора
-
проекция вектора ![]() на плоскость xy.
на плоскость xy.
Таким образом, вектор ![]() составляет с осью симметрии тела угол
составляет с осью симметрии тела угол ![]() и вращается вокруг этой
оси, как следует из (3.59), с постоянной угловой скоростью
и вращается вокруг этой
оси, как следует из (3.59), с постоянной угловой скоростью ![]() Начальная фаза
Начальная фаза ![]() этого вращения определяется начальными условиями.
этого вращения определяется начальными условиями.
Посмотрим, как будет выглядеть движение твердого тела в лабораторной системе
x0y0z0. Поскольку нам известны значения ![]() и
и ![]() то закон движения тела (зависимость углов
Эйлера от времени) в принципе может быть получен из кинематических уравнений
Эйлера (1.30-1.32). Однако это связано с решением в общем случае довольно
сложных дифференциальных уравнений, поэтому мы ограничимся качественным
рассмотрением движения тела. В силу того, что
то закон движения тела (зависимость углов
Эйлера от времени) в принципе может быть получен из кинематических уравнений
Эйлера (1.30-1.32). Однако это связано с решением в общем случае довольно
сложных дифференциальных уравнений, поэтому мы ограничимся качественным
рассмотрением движения тела. В силу того, что
| (3.60) |
(i, j, k - орты главных осей инерции тела), а ![]() можно записать
можно записать
| (3.61) |
Здесь добавлен и вычтен член ![]() что позволяет
представить (3.61) в виде
что позволяет
представить (3.61) в виде
| (3.62) |
Отсюда видно, что k (ось фигуры), L и ![]() лежат в одной
плоскости. Из (3.62) следует, что
лежат в одной
плоскости. Из (3.62) следует, что
| (3.63) |
где
| (3.64) |
есть составляющая угловой скорости по направлению L. Плоскость, в
которой лежат ось фигуры, ![]() и L, поворачивается (прецессирует)
вокруг направления L с угловой скоростью
и L, поворачивается (прецессирует)
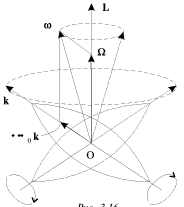
вокруг направления L с угловой скоростью ![]() называемой скоростью
прецессии (рис. 3.16). Само движение называется регулярной прецессией
свободного симметричного волчка.
называемой скоростью
прецессии (рис. 3.16). Само движение называется регулярной прецессией
свободного симметричного волчка.
 |
| Рис. 3.16. |
Отметим, что в случае веретенообразного тела, изображенного на рис. 3.16,
![]() поэтому
поэтому ![]() (см. (3.58)), и вектор -
(см. (3.58)), и вектор -
![]() направлен в ту же сторону, что и k.
направлен в ту же сторону, что и k.
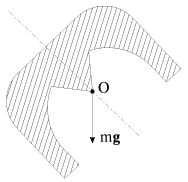
Замечание 1. Закрепление аксиально симметричного твердого тела в центре масс может быть выполнено не только с помощью карданова подвеса, но, например, так, как показано на рис. 3.17. Массивное тело, сечение которого плоскостью рисунка заштриховано, шарнирно закреплено в точке О, совпадающей с центром масс тела.
 |
| Рис. 3.17. |
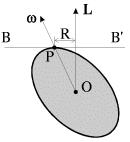
Замечание 2. Используя построение Пуансо (см. лекцию 2), регулярной прецессии свободного симметричного волчка можно дать наглядную геометрическую интерпретацию (рис. 3.18).
 |
| Рис. 3.18. |
Момент импульса L, тела относительно неподвижного центра масс О
представляет собой вектор, постоянный по величине и направлению. Эллипсоид
инерции тела с центром в точке О, сечение которого изображено на рис. 3.18,
является эллипсоидом вращения. Касательная к эллипсоиду плоскость BB'
проведена через полюс Р пересечения мгновенной угловой скорости ![]() с
эллипсоидом; эта плоскость перпендикулярна к вектору L и в
лабораторной системе отсчета сохраняет свое положение неизменным. При
регулярной прецессии волчка эллипсоид инерции тела катится по плоскости
BB' без скольжения, так что геометрическим местом полюсов Р является
окружность радиуса
с
эллипсоидом; эта плоскость перпендикулярна к вектору L и в
лабораторной системе отсчета сохраняет свое положение неизменным. При
регулярной прецессии волчка эллипсоид инерции тела катится по плоскости
BB' без скольжения, так что геометрическим местом полюсов Р является
окружность радиуса ![]() принадлежащая плоскости BB'.
принадлежащая плоскости BB'.
Замечание 3. Во избежание путаницы отметим следующее. Описанное выше
движение связано с изменением угла прецессии ![]() (см. рис. 1.3), поэтому
оно и было названо регулярной прецессией (кинематическое определение).
Однако существуют определения прецесcии как движения оси симметрии тела под
действием момента внешних сил (динамическое определение, см. лекцию 4).
Описанное же выше движение с точки зрения динамического определения называют
нутацией.
(см. рис. 1.3), поэтому
оно и было названо регулярной прецессией (кинематическое определение).
Однако существуют определения прецесcии как движения оси симметрии тела под
действием момента внешних сил (динамическое определение, см. лекцию 4).
Описанное же выше движение с точки зрения динамического определения называют
нутацией.
|
Публикации с ключевыми словами:
механика - твердое тело - углы Эйлера
Публикации со словами: механика - твердое тело - углы Эйлера | |
|
См. также:
| |