Астронет > Механика сплошных сред

по текстам по ключевым словам в глоссарии по сайтам перевод по каталогу

Механика сплошных сред

Течение вязкой жидкости. Формула Пуазейля.

Рассмотрим течение вязкой жидкости, обратившись непосредственно к опыту. Подключим тонкую горизонтальную стеклянную трубу с впаянными в нее вертикальными манометрическими трубками при помощи резинового шланга к водопроводному крану (рис. 4.6).

Рис. 4.6.

При небольшой скорости течения воды легко усматривается понижение уровня воды в манометрических трубках в направлении течения (h1>h2>h3). Это в свою очередь указывает на наличие горизонтального градиента давления - статическое давление жидкости уменьшается вдоль потока. При равномерном прямолинейном течении жидкости силы давления уравновешиваются силами вязкости, а силы инерции отсутствуют вовсе. Уравнение Навье-Стокса для этого случая запишется в виде

$- {\rm grad }\; p + \mu\Delta {\bf v} = 0.$

(4.12)

Распределение скоростей в поперечном сечении потока вязкой жидкости можно наблюдать при ее вытекании из вертикальной трубки через узкое отверстие (рис. 4.7).

Рис. 4.7.

Если, например, при закрытом кране К налить вначале подкрашенный сахарный сироп, а затем поверх осторожно налить неподкрашенный сироп, то в состоянии равновесия граница раздела Г будет горизонтальной. Если кран К открыть, то граница раздела примет форму, похожую на параболоид вращения. Это указывает на существование распределения скоростей в сечении трубки при вязком течении сиропа. Нетрудно вычислить это распределение скоростей потока в поперечном его сечении. Это можно сделать, записав уравнение (4.12) в цилиндрических координатах (x, r) и проинтегрировав его. Однако мы поступим несколько проще, если приравняем силы вязкости и давления, действующие на цилиндрический объем жидкости радиуса r и длиной dx (рис. 4.8):

$(p(x) - p(x+dx))\pi r^2 + \mu 2\pi rdx\frac{dv}{dr}=0.$

(4.13)

Отметим, что равнодействующая сил давления направлена по потоку (вдоль оси x), а сила вязкого трения, приложенная к боковой поверхности цилиндрического объема - против потока, поскольку dv/dr<0. Произведя сокращение и разделив (4.13) на dx, получаем

$-\frac{dp}{dx} + \mu\frac{2}{r}\frac{dv}{dr}=0.$

(4.14)

Величина градиента давления dp/dx в (4.14) не зависит от радиуса r, т.к. давление p=p(x) и в поперечном сечении x=const не меняется. Это позволяет проинтегрировать (4.14) по радиусу:

$\frac{dp}{dx}\int\limits_R^r rdr = 2\mu\int\limits_0^v dv.$

(4.15)

Уравнение (4.15) позволяет рассчитать распределение скоростей , при условии, что у стенок трубы эта скорость равна нулю. После интегрирования (4.15) получаем

$v(r) = -\frac{1}{4\mu}\frac{dp}{dx}(R^2 - r^2).$

(4.16)

Давление равномерно падает в направлении оси x, поэтому dp/dx<0 и не зависит от x. Параболическое распределение скоростей (4.16) графически изображено на рис. 4.8 у выходного сечения трубы. Поток вектора скорости через поперечное сечение трубы, или жидкости, протекающей через сечение в единицу времени (на практике употребляют термин "расход жидкости") оказывается равным

$N_v = \int vdS = \int\limits_0^R v(r)2\pi rdr = \frac{\pi R^4}{8\mu}\left(-\frac{dp}{dx}\right).$

(4.17)

Для практических целей расход жидкости определяют по формуле Пуазейля

$N_v = \frac{\pi R^4}{8\mu}\frac{p_1 - p_2}{\ell}.$

(4.18)

Здесь расход воды N_v пропорционален разности давлений p₁-p₂ на концах трубы длиной $\ell$ . Следует обратить внимание на существенную зависимость пропускной способности трубы от ее радиуса R. При заданном давлении на входе водопроводной сети увеличение диаметра труб вдвое влечет увеличение их пропускной способности в 16 раз!

Рис. 4.8.

Пользуясь формулой Пуазейля можно определить вязкость жидкости. Так, например, в опыте, изображенном на рис. 4.6, легко измерить разность давлений и расход жидкости и при известном радиусе горизонтальной трубки посчитать вязкость жидкости Однако более удобно вязкость жидкости определять по методу Стокса, измеряя время падения шарика в этой жидкости (см. ниже). Параболический профиль скорости слоев, как нетрудно подсчитать, будет и при течении жидкости между двумя пластинами (рис. 4.4). 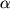Если этот рисунок разрезать посередине на высоте и наклонить нижнюю пластину под углом $\alpha$ , то мы получим картину слоистого течения воды в реке под действием силы тяжести (рис. 4.9). Вместо перепада давления dp/dx мы можем использовать компоненту силы тяжести $F_x = \rho g\sin\alpha$ при расчете профиля скоростей течения.

Рис. 4.9.

Ламинарное и турбулентное течение.

Обратимся теперь к вопросу об устойчивости течения жидкости по трубам. С этой целью поставим следующий эксперимент. Пусть жидкость вытекает из сосуда через горизонтальную стеклянную трубку (рис. 4.10). Для контроля за характером течения будем при помощи капилляра впускать ту же, но окрашенную жидкость во входное сечение трубки.

Рис. 4.10.

В случае малого поперечного сечения трубы и не очень большой скорости течения окрашенная струйка движется прямолинейно строго вдоль оси трубы (ситуация а на рис. 4.10). При большем сечении или при удвоении скорости появляется нерегулярное движение, когда струйка разбивается на множество извилистых струек (ситуация б). В первом случае движение называется слоистым, или ламинарным, а во втором случае - турбулентным. При ламинарном течении силы вязкости сглаживают боковые движения жидкости, возникающие вследствие различных неровностей стенок трубы. Инерция жидкости стремится сохранить боковые движения жидкости, способствуя тем самым турбулентности. Переход от ламинарного к турбулентному течению приводит при некотором числе Рейнольдса, получившего название критического:

${\rm Re_{кр}} = \left(\frac{\rho vR}{\mu}\right)_{кр}.$

(4.19)

Его значение сильно зависит от формы входной части трубы. В случае закругленного конца, как на рис. 4.10, течение с самого начала устанавливается ламинарным и продолжает оставаться таким до больших чисел Рейнольдса. Область критических чисел Re_кр лежит между значениями 1200 (незакругленный вход) и 20000 (закругленный вход). Поэтому в литературе приводятся весьма различные значения Re_кр.

Рис. 4.11.

При стационарном турбулентном течении скорость в данной точке случайным образом меняется во времени, однако среднее значение вектора скорости <v> направлено вдоль оси трубы. Средняя скорость остается постоянной по сечению трубы, и только в очень тонком пограничном слое спадает до нуля у стенок трубы. На практике для расчета турбулентного течения жидкости по трубе используется формула

$p_1 - p_2 = k\rho \left \lt v\right\gt^2\frac{\ell}{R},$

(4.20)

в которой k - безразмерный гидравлический коэффициент. Средняя же по сечению скорость ламинарного течения из формулы Пуазейля (4.18) получается равной

$\left\lt v\right\gt = \frac{N_v}{\pi R^2} = \frac{R^2}{8\mu}\frac{p_1 - p_2}{\ell}.$

(4.21)

Разность давлений, как функция скорости

$p_1 - p_2 = \frac{8\mu}{R}\left\lt v\right\gt\frac{\ell}{R}.$

(4.22)

Если сравнить перепады давлений для турбулентного (4.20) и ламинарного (4.22) течений, то легко видеть, что повышение скорости прокачки жидкости по трубам при турбулентном течении потребует значительно большего увеличения перепада давлений, чем при ламинарном. Известен исторический факт прокладки нефтепровода в России, спроектированного на основе формулы (4.20). Однако при приложенной разности давлений пропускная способность нефтепровода оказалась выше расчетной. Ошибка проекта (к счастью, удачная) состояла в том, что несмотря на большой диаметр труб нефтепровода вязкая нефть течет ламинарно, и пропускная способность нефтепровода должна рассчитываться по формуле (4.22). Формулы (4.20) и (4.22) можно объединить в одну, если принять, что безразмерный гидравлический коэффициент в (4.20) зависит от числа Рейнольдса: k = k₀ + 8/Re. Тогда при Re>Re_кр k $\approx$ k₀, и течение турбулентное. Напротив, при Re $\le$ 1 k $\approx$ 8/Re, и формула (4.20) переходит в (4.22). На рис. (4.12) изображен график зависимости перепада давления в трубах в зависимости от скорости течения. Однако если двигать трубу относительно неподвижной жидкости, то кривую на рис. 4.12 с известной натяжкой можно интерпретировать как зависимость силы лобового сопротивления, приходящейся на единицу площади сечения трубы, от скорости ее движения в жидкости. При малых скоростях движения сила сопротивления пропорциональна скорости, а при больших - квадрату скорости.

Рис. 4.12.

При свободном ламинарном течении (в отсутствие направляющих поверхностей) струи жидкости развиваются неустойчивости, и ламинарное течение переходит в турбулентное. На рис. 4.13. представлено оптическое изображение текущей струи жидкости (число Рейнольдса Re=250). Хорошо видно, что течение от ламинарного режима через переходный трансформируется в турбулентный. До настоящего времени нет ясного понимания, почему это происходит. Классическая линейная теория устойчивости дает верное описание начальной стадии разрушения ламинарного течения. Ясно, что переход к турбулентному течению является существенно нелинейным процессом, и теория устойчивости должна базироваться на анализе нелинейных давлений гидродинамики.

Рис. 4.13.

Мы отметим, что в области ламинарного течения линии тока практически параллельны. Поле скоростей является потенциальным (по аналогии с однородным полем силы тяжести). Описание течения может быть значительно проще, если использовать потенциал скоростей

$\Phi (r) = \int\limits_{r_0}^r v(r)dr.$

(4.23)

В ряде задач проще рассчитать сначала потенциал скоростей, а затем и скорость: v = -grad Ф В области турбулентного течения невозможно ввести однозначно потенциал скоростей. Скорость течения v в каждой точке является случайной функцией времени, и необходимо развивать статистический подход к описанию турбулентного течения. Очень плодотворным является понятие вихря. С математической точки зрения вихревой характер течения имеет место тогда, когда отлична от нуля "работа" вектора скорости v по замкнутому контуру, получившая название циркуляции вектора скорости:

$\Gamma = \oint\limits_{\ell} vd\ell \ne 0.$

(4.24)

На рис. 4.14 схематично изображены линии тока в фиксированный момент времени при турбулентном течении и показан контур $\ell$ , по которому вычисляется интеграл (4.24). Символ $\oint$ означает, что интегрирование производится по замкнутому контуру. Если размеры контура стягивать в точку, то в этой точке интенсивность вихреобразного течения будет характеризоваться ротором вектора скорости в соответствии с определением

$({\rm rot}\; {\bf v})_n = \lim_{\Delta S\to 0}\frac{\Gamma}{\Delta S}.$

(4.25)

Здесь $\Delta S$ - площадь маленького контура, n - нормаль к этой площадке, направленная туда же, куда и острие буравчика, рукоятка которого вращается в направлении течения. Формула (4.25) дает лишь значение проекции вектора rot v на направлении нормали, поскольку контур ориентирован произвольно. Чтобы посчитать компоненты вектора rot v надо вычислить циркуляции по контурам, нормали к которым совпадают с соответствующими осями координат.

Рис. 4.14.

В качестве иллюстрации к сказанному посчитаем ротор вихревого течения воды, подобно тому, которое имеет место вблизи выпускного отверстия ванны. Если принять, что частицы движутся с угловой скоростью $\omega$ , то циркуляция вектора скорости по круглому контуру радиуса r с центром на оси сливного отверстия и перпендикулярного к ней равна

$\Gamma = v\cdot 2\pi r = \omega r2\pi r = 2\pi r^2\omega.$

(4.26)

При такой ориентации контура вектор rot v будет направлен по нормали n к контуру и равен

${\rm rot}\; {\bf v}=\frac{\Gamma}{\Delta S}{\bf n } = \frac{2\pi r^2 \omega}{\pi r^2}{\bf n}= 2 {\bf \omega}.$

(4.27)

Проведем без доказательства формулу для вектора rot v в декартовых координатах:

${\rm rot}\; {\bf v}= \left( \frac{\partial v_z}{\partial y} - \frac{\partial v_y}{\partial z}\right){\bf i} + \left( \frac{\partial v_x}{\partial z} - \frac{\partial v_z}{\partial x}\right){\bf j}+ \left( \frac{\partial v_y}{\partial x} - \frac{\partial v_x}{\partial y}\right){\bf k}.$

(4.28)

Здесь i, j и k - единичные векторы вдоль соответствующих декартовых осей координат. Желающие могут подсчитать (4.27), пользуясь формулой (4.28).

Назад | Вперед

Публикации с ключевыми словами: механика - гидродинамика - газодинамика - упругость Публикации со словами: механика - гидродинамика - газодинамика - упругость
См. также: Д'Аламбера-Эйлера парадокс Механика твердого тела. Лекции. Число Маха Вариационные принципы механики Конус Маха Бернулли уравнение Баротропное явление Все публикации на ту же тему >>

Мнения читателей [4]

Версия для печати

Астрометрия - Астрономические инструменты - Астрономическое образование - Астрофизика - История астрономии - Космонавтика, исследование космоса - Любительская астрономия - Планеты и Солнечная система - Солнце