 Теорема Ампера
Теорема Ампера17.08.2001 11:17 | "Физическая Энциклопедия"/Phys.Web.Ru
Устанавливает эквивалентность
полей, создаваемых магнитным листком и
постоянным электрическим
током, текущим
по контуру, совмещенному с краем этого листка. Магнитным
листком называется участок поверхности S с равномерно
распределенными на нем
элементарными магнитными диполями, направленными
по нормали ![]() к S
(рис. 1). Поверхностная плотность
диполей
к S
(рис. 1). Поверхностная плотность
диполей ![]() на листке связана с эквивалентным током I
соотношением
на листке связана с эквивалентным током I
соотношением ![]() (Гаусса
система единиц);
при этом направления
тока и нормали
(Гаусса
система единиц);
при этом направления
тока и нормали ![]() удовлетворяют правилу
правого винта. В случае произвольного распределения вектора намагниченности
удовлетворяют правилу
правого винта. В случае произвольного распределения вектора намагниченности
![]() (дипольного момента единицы объема) плотность
эквивалентного тока
(дипольного момента единицы объема) плотность
эквивалентного тока ![]() определяется равенством
определяется равенством ![]() , являющимся
обобщением теоремы Ампера.
, являющимся
обобщением теоремы Ампера.
В 1820 А. М. Ампер экспериментально
показал, что магнитные свойства витка с током и постоянного
магнита на достаточно больших
расстояниях
одинаковы. В том же году он сформулировал и доказал теорему Ампера с помощью предвосхитившего
вывод формулы Стокса, рассуждения: пусть по замкнутому
контуру ![]() , лежащему на поверхности S,
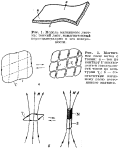
течет электрический ток I. Поверхность S можно
разбить на сколь угодно большое число ячеек (рис.
2, а) и представить, что по каждому элементу получившейся сетки текут виртуальные
токи, равные по величине I и противоположные по направлениям,
так что суммарный ток
в каждом внутреннем элементе равен нулю. В силу принципа
суперпозиции полученная система виртуальных токов эквивалентна по своему
магнитному действию
исходному току; с другой стороны, каждый элементарный виток с током эквивалентен
маленькому магнитику с дипольным моментом
, лежащему на поверхности S,
течет электрический ток I. Поверхность S можно
разбить на сколь угодно большое число ячеек (рис.
2, а) и представить, что по каждому элементу получившейся сетки текут виртуальные
токи, равные по величине I и противоположные по направлениям,
так что суммарный ток
в каждом внутреннем элементе равен нулю. В силу принципа
суперпозиции полученная система виртуальных токов эквивалентна по своему
магнитному действию
исходному току; с другой стороны, каждый элементарный виток с током эквивалентен
маленькому магнитику с дипольным моментом ![]() ,
где
,
где
![]() - площадь ячейки (рис. 2, б).
- площадь ячейки (рис. 2, б).
Теорема Ампера сыграла значительную роль в становлении представлений о
единой природе электрических и магнитных явлений. Вместе с принципом
перестановочной
двойственности теорема Ампера позволяет установить соответствие между
полями в электростатических и магнитостатических системах (![]() ); с некоторыми ограничениями его можно
перенести и на переменные поля.
); с некоторыми ограничениями его можно
перенести и на переменные поля.
|
Публикации с ключевыми словами:
электричество - теорема Ампера - магнитное поле - электрический ток
Публикации со словами: электричество - теорема Ампера - магнитное поле - электрический ток |

|
См. также:
Все публикации на ту же тему >> | |