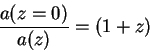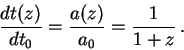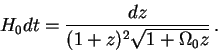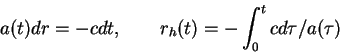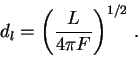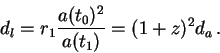---

<< 11. Космология (продолжение) | Оглавление | 11.2 Горячая Вселенная >>

Разделы

• 11.1.1 Горизонт
• 11.1.2 Угловое и фотометрическое расстояния
• 11.1.3 Поверхностная яркость и парадокс Ольберса

---

11.1 Распространение света. Красное смещение

Перейдем от обсуждения математических моделей к реально наблюдаемым величинам. Основная информация от космических объектов получается из наблюдения электромагнитных волн (света). Рассмотрим фотон частоты , испускаемый в точке с координатой на фоне расширяющейся Вселенной. Пусть приемник расположен в точке с координатой .^11.1Скорость точки 2 относительно точки 1 есть, очевидно, . Применяя нерелятивистский эффект Допплера (т.е. рассматривая не слишком удаленные точки, что на самом деле оказывается несущественным), находим разницу между принятой и испущенной частотой фотона

Устремляя получаем дифференциальное уравнение

и учитывая выражение постоянной Хаббла через масштабный фактор и интегрируя, получаем

Аналогично, энергия фотона , уменьшается в ходе расширения, температура излучения , импульс частиц , длины волн (в т.ч. де Бройлевская длина волны) . Наглядная аналогия растяжению длин волн пропорционально масштабному фактору имеется в замкнутой Вселенной, рассматриваемой как резонатор. Если есть стоячая волна с узлами, при адиабатическом расширении число узлов должно сохраняться , то есть .

Наблюдаемая величина есть красное смещение, связывающее длину волны принимаемого и испущенного фотонов:

Интерпретируя красное смещение как результат эффекта Допплера, , , Хаббловская зависимость для малых z может быть записана в виде

где - постоянная Хаббла, характеризующая скорость расширения Вселенной в настоящий момент времени, - расстояние до объекта. Пример Хаббловских диаграмм для сверхновых типа Ia (см. в Лекции 10).

Подчеркнем еще раз, что наблюдаемой величиной в космологии является красное смещение в спектрах каких-либо объектов. Масштабный фактор на красном смещении связан с масштабным фактором наблюдателя при как

(Вселенная расширяется, поэтому в прошлом (т.е. на больших красных смещениях) масштабный фактор был меньше).

Из  (11.3) также следует, что интервал собственного времени (т.е. времени, измеренного по сопутствующим часам) на красном смещении измеряется наблюдателем как интервал

Из-за расширения Вселенной время, измеренное по часам сегодняшнего наблюдателя, в прошлом течет "быстрее".

Зависимости наблюдаемых величин (например, красного смещения от расстояния) становятся нелинейными на больших расстояниях и требуют уточнения параметров космологической модели (полная плотность вещества , величина космологической постоянной и т.д.)

Связь времени распространения света до наблюдателя, находящегося по определению в точке с , с расстояний, соответствующих красному смещению , находится из соотношения (11.6) и во Фридмановских моделях без космологической постоянной осуществляется по формуле:

Здесь - полная плотность в единицах критической, - современное значение постоянной Хаббла. Зависимость времени от красного смещения таким образом сильно нелинейная. Интегрирование этого уравнения по в пределах от до дает полное время (называемое тж. Хаббловским временем), прошедшее с момента начала Фридмановского расширения. Для плоского мира без космологической постоянной, например, .

Пример: в плоской Вселенной без космологической постоянной объекту на красном смещении соответствует время с момента начала расширения . Для получаем , т.е. такие объекты образовались лет тому назад.

Максимальное красное смещение галактик, измеренное по линиям в их спектрах, порядка 5. Фотометрически измеренное красное смещение некоторых галактик, обнаруженных в 1998 г. при глубоком обзоре неба с борта космического телескопа им. Хаббла, около 10.

11.1.1 Горизонт

Поставим вопрос: с каких расстояний можно в принципе принимать информацию в расширяющейся Вселенной, иными словами, каков размер причинно-связанной области во Вселенной? Горизонт событий определяется как поверхность сферы, образованной совокупностью частиц, испустивших свет в момент времени t = 0, который принимается наблюдателем в момент времени . Уравнение распространения света в метрике Фридмана-Робертсона-Уокера принимает вид (угловые переменные )

и уравнение горизонта

(поставлен знак минус т.к. луч распространяется от периферии к центру). Пример. Рассмотрим плоский мир, , пылевая стадия, , , физический размер горизонта в современную эпоху ; радиационно-доминированная стадия , , . Таким образом, во фридмановской космологии горизонт всегда растет линейно со временем , в то время как масштабный фактор растет более медленно (из-за замедляющего действия гравитации): , , и рано или поздно любая точка в расширяющейся Вселенной оказывается под горизонтом, т.е. в причинно-связанной области. Обратно, уходя в прошлое замечаем, что масштабный фактор в некоторый момент растет быстрее горизонта (в пределе , . Это приводит к одному из парадоксов классической космологии, который решается в модели инфляционной Вселенной (см. Лекцию 12).

11.1.2 Угловое и фотометрическое расстояния

Понятие расстояния в расширяющейся Вселенной, описываемой метрикой Фридмана-Робертсона-Уокера, требует пояснения. Так, его можно определять по угловому размеру источника со стандартными размерами (угловое расстояние), или по принимаемому от стандартного источника потоку излучения (фотометрическое расстояние), или по собственному движению источника со стандартной скоростью (метрическое расстояние). Очевидно, в плоском пространстве-времени все три способа дадут один и тот же результат. Но Вселенная описывается искривленным пространством-временем (даже если трехмерное пространство евклидово!) с изменяющимся масштабным фактором, поэтому указанные способы дадут существенно различные значения уже при .

11.1.2.1 Угловое расстояние

В евклидовой геометрии определим угловое расстояние как расстояние, вычисляемое по видимому угловому размеру объекта : , где - собственный размер объекта перпендикулярно к лучу зрения. Пусть свет был испущен в момент времени (это время задается условием, что свет принимается сегодня, т.е. при , на ), а координата объекта была (NB: координата объекта не изменяется в ходе космологического расширения!). Собственное расстояние получается из соотношения для интервала при : . Без потери общности полагаем . Считая угол малым, из элемента метрики находим , и т.о.

или с учетом связи ( - красное смещение, соответствующее времени испускания сигнала )

Величина также имеет размерность расстояния и смысл "метрического расстояния" до источника с координатой в момент приема сигнала.

Из этих рассуждений также получаем зависимость угла, под которым виден источник с собственным размером , от красного смещения

Отметим, что вблизи горизонта , , , , т.е. угол , под которым виден удаляющийся объект конечных размеров, в расширяющейся Вселенной с любой геометрией должен проходить через минимум. Наглядная аналогия существует в замкнутом мире с постояннной положительной кривизной с топологией поверхности сферы. Там минимум достигается на "экваторе" наблюдателя.

11.1.2.2 Фотометрическое расстояние

Можно определить расстояние до объекта и по-другому: пусть объект имеет постоянную собственную светимость , а принимаемый поток излучения от него . Положим по определению фотометрическое расстояние до объекта

В расширяющейся Вселенной

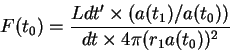
откуда, используя связь  (11.6), получаем

Можно предложить более физический вывод этого соотношения. Поток излучения от некоторого источника уменьшается из-за геометрического фактора, так как распределяется по поверхности сферы , но из-за расширения Вселенной появлется еще и дополнительная зависимость от красного смещения . Одна степень получается из-за покраснения фотона (уменьшение его частоты, собственно красное смещение), еще одна степень - за счет уменьшения частоты прихода отдельных фотонов (растяжение времени). В итоге получаем для интегрального потока

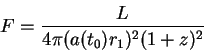
и таким образом по определению .

Обратите внимание, что на горизонте , но теперь ! В отличие от углового расстояния, фотометрическое расстояние монотонно растет с красным смещением.

11.1.3 Поверхностная яркость и парадокс Ольберса

Поверхностную яркость источника можно определить как поток излучения, принимаемый детектором от всего источника, отнесенный к телесному углу, который занимет источник на небе. По сути дела это есть не что иное, как интенсивность излучения (см. Лекцию 2). В Евклидовой геометрии телесный угол меняется с удалением от источника как , поток также уменьшается с расстоянием как , т.е. поверхностная яркость должна оставаться постоянной (теорема о сохранении интенсивности вдоль луча зрения). Какова ситуация в расширяющейся Вселенной? Выше мы показали, что линейный угол , т.е. телесный угол . Интегральный же поток излучения , откуда получаем

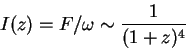
[Это соотношение более формально можно получить из Лоренц-инвариантности величины ].

Важное практическое применение этой формулы состоит в объяснении знаменитого парадокса Ольберса (XIXв), согласно которому в бесконечной Вселенной, заполненной звездами, рано или поздно должен наступить момент, когда все небо полностью перекрывается дисками звезд. Это противоречит известному факту, что ночью небо темное. Разрешение этого парадокса в рамках модели расширяющейтся Вселенной тривиально - свечения неба не наступает из-за значительного ослабления интенсивности с красным смещением. К тому же звезд и галактик не было на больших красных смещениях (первые звезды образовались из-за гравитационной неустойчивости при ), и перекрытия неба дисками тоже звезд нет.

---

<< 11. Космология (продолжение) | Оглавление | 11.2 Горячая Вселенная >>

Публикации с ключевыми словами: звезды - Межзвездная среда - Космология - теоретическая астрофизика - астрофизика Публикации со словами: звезды - Межзвездная среда - Космология - теоретическая астрофизика - астрофизика
См. также: Местное межзвездное облако Черная дыра разрушает звезду: анимация Звезды, пыль и туманность в NGC 6559 25 самых ярких звезд на ночном небе Анимация: черная дыра разрушает звезду Разложение далекого света Сравнение размеров звезд Все публикации на ту же тему >>