---

<< 6. Звезды (продолжение) | Оглавление | 7. После главной последовательности >>

Разделы

• 6.1.1 Ядерные реакции в звездах
• 6.1.2 Особенности ядерных реакций в звездах
• 6.1.3 Замечания о фотонной светимости Солнца
• 6.1.4 Соотношения масс-светимость и масса-радиус для звезд главной последовательности

---

6.1 Звезды. Строение и эволюция. (продолжение)

6.1.1 Ядерные реакции в звездах.

Запасы ядерной энергии в звездах намного превышают запас тепловой энергии. Если бы звезда (например, Солнце) светила только за счет гравитационого сжатия, то по теореме вириала время высвечивания тепловой энергии (время Кельвина-Гельмгольца)

Запас ядерной энергии , где - масса ядра звезды, где могут идти термоядерные реакции, - энреговыделение на единицу массы (эффективность) ядерных реакций. При синтезе гелия из водорода (происходит на стадии главной последовательности звезд на диаграмме Герцшпрунга-Рессела) суммарная реакция (как в протон-протонном, так и в CNO-цикле) сводится к образованию одного ядра гелия из 4-х протонов, . Выделяемая энергия при этом - дефект массы:

т.е. примерно 7 МэВ на нуклон. Как увидим ниже, не вся выделяющаяся энергия идет в тепло, небольшая часть (0.6 МэВ) уносится нейтрино, для которого Солнце прозрачно. Энергия покоя нуклона почти 1 ГэВ, т.е. эффективность синтеза гелия из водорода Следовательно, характерное время длительности стадии главной последовательности

(здесь учтено эмпирическое соотношение масса-светимость для звезд главной последовательности , доказательство которого приводится в конце этой лекции).

Замечания:

1. сильная зависимость от массы звезды (примерно как ) - так, звезда с массой в 10 солнечных эволюционирует в 100 раз быстрее Солнца!

2. стадия термоядерного горения водорода в ядре звезды - самая длительная. Все последующие стадии (горение гелия в углерод и т.д.) составляют всего лишь от . Это связано с тем, что скорости термоядерных реакций очень чувствительны к температуре, а для реакций синтеза более тяжелых элементов температура в ядре болжна быть выше (требуется преодоление более высокого Кулоновского барьера ).

6.1.2 Особенности ядерных реакций в звездах.

Используя теорему вириала , центральная температура в звезде может быть оценена как

Здесь - универсальная газовая постоянная, - молекулярный вес вещества. Для полностью ионизованной плазмы солнечного химсостава . Т.е. средняя кинетическая энергия частиц в центре Солнца кэВ. С другой стороны, чтобы пошла реакция соединения двух протонов в ядро дейтерия, требуется преодолеть кулоновский барьер МэВ (здесь учли, что реакция пойдет при приближении протонов на расстояние действия ядерных сил см).

Газ в центре Солнца вполне идеален, и частицы (протоны) движутся со скоростями в соответствии с Максвелловским распределением . Отсюда доля протонов с энергией оказывается , что безнадежно мало даже для солнечной массы с числом частиц .

Как было впервые показано Г.А.Гамовым, ядерные реакции в центре Солнца все же возможны из-за эффекта квантовомеханического туннелирования волновой функции под кулоновский барьер. Импульс частицы в квантовой механике (Де Бройль) , где - волновое число. Движение частицы с зарядом с импульсом соответствует волновая функция . Кинетическая энергия частицы , где - потенциальная энергия в кулоновском поле c зарядом . Отсюда . В классической механике при происходит отражение частицы от барьера, т.е. частица не проникает в область . В квантовой механике при имеем и волновая функция . Это означает, что всегда есть отличная от нуля вероятность подбарьерного перехода

Здесь

постоянная, называемая Гамовской энергией. Интегрируя по максвелловскому распределению частиц с энергией , получаем скорость реакции

Интеграл легко берется методом перевала. Не имея здесь места для более подробного изложения, отошлем интересующихся к великолепной монографии Д.А.Франк-Каменецкого "Физические процессы внутри звезд", М.:Физматгиз, 1959. Окончательный ответ:

где

и численно

где температура выражена в миллиардах градусов  K. Полученный закон роста скорости реакций с температурой отражает увеличение вероятности просачивания через барьер и уменьшение доли числа частиц с требуемой энергией.

Знание скорости реакции позволяет легко рассчитать изменение концентрации взаимодействующих элементов со временем:

или в терминах долей массы соответствующих элементов

Отметим линейную (а не квадратичную) зависимость от плотности , т.к. расчет ведется на единицу массы.

Рассмотрим теперь некоторые особенности основных термоядерных реакций, происходящих в звездах главной последовательности.

6.1.2.1 pp-цикл (Г.Бете, 1939)

Реализуется в звездах небольших масс .

1.

2.

3. (65%)

или (35%)

4. (35%)

или (0.1%)

5.

Замечания:

1. 1-я реакция самая медленная, т.к. идет по каналу слабого взаимодействия, в гамильтониан входит постоянная Ферми . Она определяет темп энерговыделения и время жизни на главной последовательности.

2. Дейтерий (2-я реакция) быстро вступает в реакцию с образованием гелия-3, равновесная концентрация определяется отношением времен реакций (1) и (2), т.е. . Это важное свойство дейтерия быстро "выгорать" в звездах позволяет считать дейтерий в межзвездной среде первичным, т.е. образованным при первичном нуклеосинтезе в ранней Вселенной. Измерение содержания первичного дейтерия - важнейший тест теории первичного нуклеосинтеза.

3. Эффективность энерговыделения на грамм вещества зависит от температуры в высокой степени:
   

   (6.8)

   
   
   ( - плотность; входит в первой степени т.к. расчет энерговыделения ведется на единицу массы). Отметим низкую среднюю "калорийность" ядерных реакций:  эрг/г/с - примерно энерговыделение в процессе гниения опавшей листвы в осеннем саду...

4. Нейтрино в среднем уносят энергию 0.6 МэВ. Количество нейтрино , излучаемое Солнцем за секунду, определяется только светимостью Солнца, т.к. в термоядерных реакциях в Солнце при выделении 26.7 МэВ рождается 2 нейтрино, откуда нейтрино/с. Поток р-р нейтрино на Земле частиц/см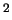/c.

5. Прямая проверка теории - наблюдение солнечных нейтрино. Нейтрино высоких энергий (борные) регистрируются в хлор-аргонных экспериментах (эксперименты Дэвиса), и устойчиво показывают недостаток нейтрино по сравнению с теоретическим значением для стандартной модели Солнца. Нейтрино низких энергий, возникающие непосредственно в рр-реакции, регистрируются в галлий-германиевых экспериментах (GALLEX в Гран Сассо (Италия-Германия) и SAGE на Баксане (Россия - США). Результаты этих экспериментов также постоянно показывают дефицитт наблюдаемого потока нейтрино (по результатам 1990-1995 гг. измеренный поток нейтрино составляет SNU, в то время как в стандартной модели ожидается 122 SNU). Если нейтрино имеют отличную от нуля массу покоя (современное ограничение из эксперимента эВ), возможны осцилляции (превращения) различных сортов нейтрино (эффект Михеева-Смирнова-Вольфенштейна) друг в друга или в правополяризованные (стерильные) нейтрино, которые не взаимодействуют с веществом. Мюонные и тау-нейтрино имеют гораздо меньшие сечения взаимодействия с веществом, чем электронное нейтрино, поэтому наблюдаемый дефицит может быть объяснен, не меняя стандартной модели Солнца, построенной на основе всей совокупности астрономических данных.

6.1.2.2 CNO-цикл

Реализуется в звездах массивнее Солнца. В этой цепочке реакций углерод выступает в роли катализатора, т.е. в конечном счете и в CNO-цикле .

Замечания

1. Энерговыделение на единицу массы сильно зависит от температуры:

2. Cуммарное энерговыделение в обоих циклах примерно одинаково:

   
   

   
   
   

   
   

   
   
   

   В CNO-цикле нейтрино уносят несколько больше энергии, чем в водородном (т.к. реакции идут при более высокой температуре).

6.1.3 Замечания о фотонной светимости Солнца

Фотоны рождаются в зоне ядерных реакций в недрах Солнца. Плотность вещества центре Солнца около 120 г/см, температура около 1 кэВ. Условия с высочайшей точностью соответствуют полному термодинамическому равновесию, поэтому энергия рождающихся фотонов распределена по закону Планка для АЧТ с температурой 1 кэВ (рентгеновский диапазон). Если нейтрино, имеющее ничтожное сечение взаимодействия с веществом ( см) свободно (за время c) покидают Солнце, то фотоны многократно поглощаются и рассеиваются^6.2, пока достигнут внешних более прозрачных слоев атмосферы Солнца. Видимая "поверхность" Солнца - поверхность оптической толщины (опт. толщина отсчитывается от наблюдателя вглубь Солнца) - т.н. фотосфера, ее эффективная температура, определяемая из соотношения , K и определяет физическое состояние внешних слоев Солнца. Температура быстро растет с глубиной.

При малых отклонениях от термодинамического равновесия (когда длина свободного пробега фотонов мала по сравнению с размерами рассматриваемой области) перенос лучистой энергии хорошо описывается диффузионным приближением. В этом приближении

[поток энергии] = -[коэффициент диффузии]  [плотность энергии]:

Здесь коэффициент диффузии , средняя длина свободного пробега фотонов определяется коэффициентом непрозрачности  [см/г]

Например, для не слишком горячей плазмы основную роль играет тормозное (свободно-свободное) поглощение

и усредненная непрозрачность (т.н. Крамерсовская непрозрачность)

В общем случае коэффициент непрозрачности может быть записан как степенная функция от плотности и температуры вещества , где показатели степени зависят от химического состава плазмы и ее температуры. Зависимость от температуры может быть как обратная, так и прямая, т.е. непрозрачность может как уменьшаться, так и увеличиваться с ростом температуры в зависимости от физического состояния плазмы. На этом основан механизм пульсации некоторых переменных звезд (цефеид).

В горячих звездах большой массы основную роль играет рассеяние на свободных электронах. Поскольку в нерелятивистском пределе Томсоновское рассеяние не зависит от частоты кванта, томсоновская непрозрачность постоянна,

Для плотности энергии равновесного излучения имеем

а поток энергии в сферически-симметричном случае связан со светимостью на данном радиусе соотношением

поэтому уравнение  (6.9) можно переписать в виде обыкновенного дифференциального уравнения для температуры

Пример: время диффузии фотонов из центра Солнца.

Пока температура среды высока (больше 2 млн. градусов) энергия переносится лучистой теплопроводностью (фотонами). Основной вклад в непрозрачность обусловлена рассеянием фотонов на электронах (томсоновское рассеяние, см, непрозрачность см/г. Эта зона простирается примерно до 2/3 радиуса Солнца (  см. Время диффузии фотонов из ядра до границы конвективной зоны , где - коэффициент диффузии, - длина свободного пробега фотона. Получаем:

При понижении температуры непрозрачность солнечного вещества сильно возрастает (см. закон Крамерса  (6.12)), поэтому диффузия фотонов длится около миллиона лет. Далее непрозрачность вещества (гл. образом из-за многочисленных линий железа и других тяжелых элементов) становится настолько большой ( см/г), что возникают крупномасштабные конвективные движения - 1/3 радиуса Солнца занимает конвективная зона. Время подъема конвективной ячейки сравнительно невелико, несколько десятков лет.

Этот пример показывает, что время выхода тепловой энергии из недр Солнца (лучистая теплопроводность + конвекция) порядка миллиона лет. Это время примерно в 30 раз меньше времени Кельвина-Гельмгольца, в соответствии с долей энергии фотонов в полной энергии Солнца (продумайте последнее утверждение!).

Существенную роль на Солнце играет магнитное поле. Из-за вмороженности поля в плазму в области выхода силовых трубок магнитного поля на поверхности конвекция подавлена, перенос излучения замедлен и мы наблюдаем области пониженной температуры - пятна, эффективная температура в которых около 2000 К.

6.1.4 Соотношения масс-светимость и масса-радиус для звезд главной последовательности

Из наблюдений двойных звезд определяются массы компонент, поэтому существует возможность установления эмпирической зависимости масса-светимость. Оказалось, что для звезд главной последовательности , начиная со звезд солнечной массы, и . Эти зависимости были теоретически объяснены английским астрофизиком А.С.Эддингтоном в 1926 г.

В основе рассмотрения находится уравнение лучистой теплопроводности (6.9) или его эквивалентная форма (6.14), котрое показывает, что фотонная светимость звезды регулируется непрозрачностью ее оболочки. Для порядковых оценок заменим производные по радиусу делением на радиус , а температуру звезды заменим ее значением в центре , где возьмем из теоремы вириала. Тогда опуская постоянные (кроме постоянной тяготения) получаем

Если непрозрачность слабо зависит от параметров (а это действительно так, в горячей плазме, когда основной вклад в поглощение вносит рассеяние на свободных электронах,  смг), то получается , что и наблюдается в массивных звездах. Для Крамерсовского закона непрозрачности (6.12) получится более крутая зависимость от массы, что также подтверждается наблюдениями.

Обратите внимание на крутую зависимость от постоянной тяготения Ньютона - она может быть использована для получения ограничений на некоторые физические теории, в которых изменяется со временем. Если бы изменялась со временем, то при прочих равных условиях изменялась бы светимость Солнца. Само существования мирового океана в течение миллиардов лет на Земле (необходимое условие для органической жизни) ограничивает вариации средней температуры Земли грубо  K, т.е. . Поскольку , то из факта наличия жизни на Земле немедленно получаем за 10 лет, то есть  лет.

Теперь рассмотрим зависимость масса-радиус для звезд главной последовательности. Воспользуемся полученным соотношением (6.15). С другой стороны, светимость звезды связана с генерацией энергии в термоядерных реакциях, то есть

где Ze - число Зельдовича (показатель степенной зависимости энерговыделения на единицу массы от температуры), Ze для протон-протонного цикла. Приравнивая это выражение к (6.15) и подставляя в из теоремы вириала, получаем

где показатель степени . Так, для =const . Чем больше масса звезды на главной последовательности, тем больше ее радиус и светимость и выше эффективная температура. По этой причине звезды ранних спектральных классов (О,B,A,F) лежат левее Солнца на диаграмме Герцшпрунга-Рессела (цвет-светимость), так как цвет (спектральный класс) звезды определяется ее эффективной температурой.

Резюмируя этот раздел, еще раз подчеркнем, что основной физический параметр стационарной звезды - ее масса. Она оределяет светимость звезды на главной последовательности, время жизни, радиус, эффективную температуру. Следующий по важности параметр - химический состав, определяющий молекулярный вес вещества и влияющий на непрозрачность, а через них - и на остальные параметры. Однако в рамках нашего общего рассмотрения мы ограничимся лишь констатацией этого факта.

---

<< 6. Звезды (продолжение) | Оглавление | 7. После главной последовательности >>

Публикации с ключевыми словами: звезды - Межзвездная среда - Космология - теоретическая астрофизика - астрофизика Публикации со словами: звезды - Межзвездная среда - Космология - теоретическая астрофизика - астрофизика
См. также: Черная дыра разрушает звезду: анимация Звезды, пыль и туманность в NGC 6559 25 самых ярких звезд на ночном небе Анимация: черная дыра разрушает звезду Разложение далекого света Сравнение размеров звезд Самая далекая из всех известных звезд? Все публикации на ту же тему >>