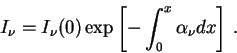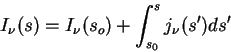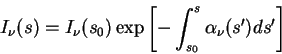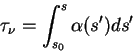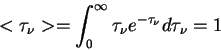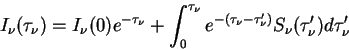<< 2.1 Уравнение переноса | Оглавление | 2.3 Тепловое излучение >>
- 2.2.1 Коэффициент излучения
- 2.2.2 Коэффициент поглощения
- 2.2.3 Уравнение переноса излучения излучения
- 2.2.4 Оптическая толща. Связь с длиной свободного пробега
- 2.2.5 Функция источника
- 2.2.6 Формальное решение уравнения переноса
2.2 Уравнение переноса излучения
Перейдем к описанию распространения излучения в среде, с которой взаимодействует излучения. Взаимодействие излучения и вещества можно рассматривать на различных физических уровнях. Для наших целей будет достаточно введения макроскопичесских коэффициентов излучения и поглощения света, хотя расчет самих коэффициентов как фцнкцию частоты фотона и физических характеристик среды проводится классическими электродинаическими и квантовыми методами.
2.2.1 Коэффициент излучения
Коэффициентом излучения называется
энергиия, излучаемая единицей объема за единицу времени
в интервале частот ![]() в направлении
в направлении ![]() :
:
В излучающей среде без поглощения
за время ![]() фотоны проходят путь
фотоны проходят путь ![]() и добавка к интенсивности из элементарного
объема
и добавка к интенсивности из элементарного
объема ![]() будет
будет
![]() . Таким образом,
уравнение переноса приобретает вид
. Таким образом,
уравнение переноса приобретает вид
2.2.2 Коэффициент поглощения
При прохождении пути ![]() в поглощающей среде часть фотонов
выбывает из пучка (поглощается), и таким образом
феноменологически можно записать
в поглощающей среде часть фотонов
выбывает из пучка (поглощается), и таким образом
феноменологически можно записать
![]() ,
где
,
где
![]() - коэффициент поглощения,
зависящий от физических параметров среды. Интенсивность пучка
уменьшается после прохождения расстояния
- коэффициент поглощения,
зависящий от физических параметров среды. Интенсивность пучка
уменьшается после прохождения расстояния ![]() от точки
от точки ![]() до
точки
до
точки ![]() по экспоненциальному закону
по экспоненциальному закону
Иногда вводят коэффициент поглощения на грамм
пройденного вещества,
![]() . В этом случае
коэффициент
. В этом случае
коэффициент ![]() см
см![]() /г называется
коэффициентом непрозрачности.
Физический смысл коэффициента непрозрачности прост.
Отнесенный к одному атому, этот коэффициент зависит только от
свойств самого атома. Эта величина
/г называется
коэффициентом непрозрачности.
Физический смысл коэффициента непрозрачности прост.
Отнесенный к одному атому, этот коэффициент зависит только от
свойств самого атома. Эта величина
![]() (
(![]() - плотность числа частиц)
имеет размерность см
- плотность числа частиц)
имеет размерность см![]() и носит название эффективного сечения
поглощения. Пусть параллельный пучок света с частотой
и носит название эффективного сечения
поглощения. Пусть параллельный пучок света с частотой ![]() с
сечением 1 см
с
сечением 1 см![]() проходит через поглощающий газ. Поглощение можно
представить себе так, будто каждый атом заменен неким малым непрозрачным
диском, перпендикулярным к направлению пучка, попадая в который квант
застревает (поглощается). Если площадь каждого диска
проходит через поглощающий газ. Поглощение можно
представить себе так, будто каждый атом заменен неким малым непрозрачным
диском, перпендикулярным к направлению пучка, попадая в который квант
застревает (поглощается). Если площадь каждого диска ![]() ,
а концентрация
,
а концентрация ![]() в куб. см, то полная площадь всех дисков
в слое газа с площадью 1 см
в куб. см, то полная площадь всех дисков
в слое газа с площадью 1 см![]() и толщиной
и толщиной ![]() равна
равна
![]() .
отсюда непосредственно получаем
.
отсюда непосредственно получаем
![]() .
.
ЗАМЕЧАНИЕ: коэффициент поглощения может быть как положительным (истинное поглощение), так и отрицательным, т.к. в элементарных процессах испускания и поглощения света атомами всегда есть вынужденное (индуцированное) излучение, пропорциональное, как и поглощение, падающей интенсивности. Хорошо известный пример из оптики - квантовый генератор излучения (лазер). В космических условиях также возможно образование инверсной заселенности уровней (комические мазеры). Мы обсудим этот вопрос подробне в лекции, посвященной межзвездной среде.
2.2.3 Уравнение переноса
Если среда способна как излучать, так и
поглощать свет, то, полагая коэффициенты
излучения ![]() и поглощения
и поглощения ![]() известными функциями координат и времени,
зависящими от физического состояния вещества (температуры,
плотности, химического состава и т.д.), в стационарном случае
можем записать
2.2
известными функциями координат и времени,
зависящими от физического состояния вещества (температуры,
плотности, химического состава и т.д.), в стационарном случае
можем записать
2.2
Замечание 1. Фотоны из пучка могут исчезать не только из-за истинного поглощения, но и из-за рассеяния (во многих реальных условиях, например, в солнечной короне, преобладает рассеяние на свободных электронах). Тогда ситуация значительно усложняется, поскольку рассеяние изменяет траектории фотонов, и уравнение переноса превращается в интегро-дифференциальное уравнение, которое решается, как правило, численными методами.
Замечание 2. Простейшие частные случаи уравнения переноса (2.15):
1. Пусть среда только излучает, ![]() ,
,
![]() ,
,
2. Пусть среда только поглощает, ![]() ,
,
![]()
2.2.4 Оптическая толща. Связь с длиной свободного пробега
Введем безразмерную характеристику вдоль луча распространения
света - оптическую толщину среды:
(иногда отсчет расстояния ведется в обратном направлении от наблюдателя к источнику, тогда в определении оптической толщи появляется знак минус).
Если ![]() , то реализуется
оптически толстый случай (среда непрозрачна
для излучения);
если
, то реализуется
оптически толстый случай (среда непрозрачна
для излучения);
если ![]() - оптически тонкий случай (среда прозрачна для
излучения).
- оптически тонкий случай (среда прозрачна для
излучения).
Важность понятия оптической толщи вытекает из ее связи
с длиной свободного пробега фотона. Рассмотрим
однородную среду без излучения. Уравнение переноса можно переписать
в виде
![]() , т.е. вероятность фотону пройти длину,
соответствующую
, т.е. вероятность фотону пройти длину,
соответствующую ![]() ,
есть
,
есть ![]() , при этом средняя оптическая толща
, при этом средняя оптическая толща
Средняя длина свободного пробега фотона
определяется из условия
![]() ,
,
2.2.5 Функция источника
Уравнение переноса (2.15) запишем в виде:
где
![]() - функция источника.
Целесообразность введения этой функции связана с тем, что
часто она находится или вычисляется проще, чем микроскопические
коэффициенты излучения или поглощения.
Как увидим ниже, для теплового излучения
функция источника представляет собой функцию Планка для
равновесного излучения.
- функция источника.
Целесообразность введения этой функции связана с тем, что
часто она находится или вычисляется проще, чем микроскопические
коэффициенты излучения или поглощения.
Как увидим ниже, для теплового излучения
функция источника представляет собой функцию Планка для
равновесного излучения.
2.2.6 Формальное решение уравнения переноса
Умножив уравнение (2.22)
на интегрирующий множитель ![]() , получаем решение
, получаем решение
Физический смысл этого решения прост. 1-е слагаемое:
начальное излучение уменьшилось в ![]() раз
из-за поглощения; 2-е слагаемое: источник, проинтегрированный
вдоль луча зрения с учетом поглощения.
раз
из-за поглощения; 2-е слагаемое: источник, проинтегрированный
вдоль луча зрения с учетом поглощения.
Это решение показывает важность определния функции источника как функции оптической глубины. Если она известна, решение выписано выше (2.23). Однако во многих реальных ситуациях функция источника заранее неизвестна, поэтому решение уравнения переноса является сложной задачей.
Рассмотрим несколько важных примеров.
Пример 1. Пусть функция источника постоянна в среде, т.е.
не зависит от оптической глубины,
![]() . Тогда
. Тогда
Это решение имеет простой физический смысл:
1) в пределе больших оптических
толщин
![]() интенсивность излучения
становится равной функции источника
интенсивность излучения
становится равной функции источника
![]() .
(Осторожнее! Если в среде есть рассеяние, то интенсивность
сама дает вклад в функцию источника, и
картина сильно усложняется).
2) Если
.
(Осторожнее! Если в среде есть рассеяние, то интенсивность
сама дает вклад в функцию источника, и
картина сильно усложняется).
2) Если ![]() , то
, то ![]() ,
, ![]() уменьшается вдоль луча
3) Если
уменьшается вдоль луча
3) Если ![]() , то
, то ![]() ,
, ![]() возрастает вдоль луча
Заключение: Интенсивность ВСЕГДА стремится к функции источника
возрастает вдоль луча
Заключение: Интенсивность ВСЕГДА стремится к функции источника
Пример 2: Образование спектральных линий.
Спектральные линии (излучения или поглощения)
образуются тогда, когда есть выделенные частоты, на которых
микроскопические коэффициенты излучения
![]() и поглощения
и поглощения ![]() как функции частоты имеют экстремумы.
Пусть, например, коэффициент
поглощения имеет острый максимум на частоте
как функции частоты имеют экстремумы.
Пусть, например, коэффициент
поглощения имеет острый максимум на частоте ![]() .
Пусть для простоты функция источника не меняется с глубиной.
Возможны несколько
вариантов наблюдаемого излучения.
.
Пусть для простоты функция источника не меняется с глубиной.
Возможны несколько
вариантов наблюдаемого излучения.
2а). Среда оптически толстая на всех частотах ![]() .
Линий нет, виден непрерывный спектр.
.
Линий нет, виден непрерывный спектр.
2б). Среда оптически тонкая, ![]() на всех частотах, фоновой
подсветки нет (
на всех частотах, фоновой
подсветки нет (![]() ). В соответствии с (2.24), наблюдается
линия излучения на частоте
). В соответствии с (2.24), наблюдается
линия излучения на частоте ![]() , причем ее максимальная
интенсивность меньше функции источника
, причем ее максимальная
интенсивность меньше функции источника
![]() .
.
2в). Ничего качественно не изменяется в случае, если
есть фоновая подсветка
![]() .
.
2г). Качественно иная картина, если фоновая подсветка больше функции
источника
![]() - появляется линия поглощения.
- появляется линия поглощения.
2д)-2е). Для случая большой оптической толщи в центре линии,
![]() , картина качественно не меняется, за исключением
достижения в линии величины функции источника.
, картина качественно не меняется, за исключением
достижения в линии величины функции источника.
Эти случаи проиллюстрированы на Рис. (2.3).
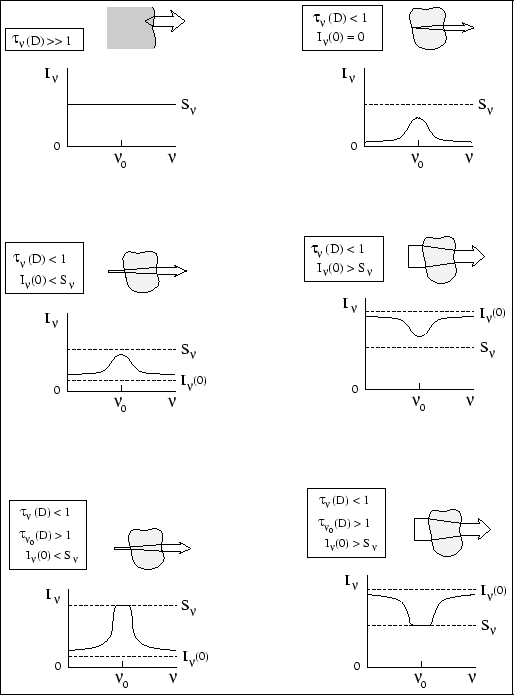 |
| Рис. 2.1
Образование спектральных линий в однородных облаках.
Линии не образуются, когда облако оптически толстое (слева вверху).
В оптически тонком облаке линии образуются только
если оно "подсвечено"
( |
<< 2.1 Уравнение переноса | Оглавление | 2.3 Тепловое излучение >>
|
Публикации с ключевыми словами:
звезды - Межзвездная среда - Космология - теоретическая астрофизика - астрофизика
Публикации со словами: звезды - Межзвездная среда - Космология - теоретическая астрофизика - астрофизика | |
См. также:
Все публикации на ту же тему >> | |