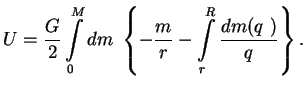Rambler's Top100Astronet    
  по текстам   по ключевым словам   в глоссарии   по сайтам   перевод   по каталогу 		 

На первую страницу
Физические основы строения и эволюции звезд
<< 1.3 Сферически-симметричные поля тяг... | Оглавление | 1.5 Давление газа ... >>

1.4 Энергия гравитационного взаимодействия


Мы видели, что энергия гравитационного взаимодействия $ U$ для двух масс $ m_1$ и $ m_2$ равна $ U=-{Gm_1m_2\over r}$. На случай $ N$ точечных масс выражение для $ U$ обобщается следующим образом:

$\displaystyle U=\sum_{\begin{array}{rcl}i,k\\ i>k\\ \end{array}}^N -\,{Gm_im_k\over r_{ik}}. $

При таком определении $ U$ каждая пара $ m_i,\;m_k$ входит в сумму только один раз. Введем величину

$\displaystyle \varphi_k=-\sum_{i\ne k}^N {Gm_i\over r_{ik}}\;, $

что, очевидно, представляет собой гравитационный потенциал, создаваемый в $ k$-той точке всеми остальными массами. Теперь для $ U$ можно написать

$\displaystyle U={1\over 2}\sum_{k=1}^N \varphi_km_k. $

Коэффициент $ {1\over 2}$ появился вследствие того, что каждая пара точек входит в сумму два раза. Это выражение легко обобщить на случай непрерывной среды:

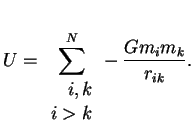
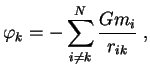
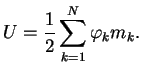
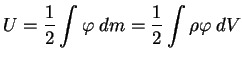
$\displaystyle U={1\over 2}\int \varphi \;dm={1\over 2}\int \rho \varphi\;dV $

(по определению $ dm=\rho \;dV$).

Для точечных масс необходимо было отбрасывать энергию самодействия, оговаривая правило суммирования. В сплошной среде самодействие не учитывается автоматически. По порядку величины $ dV \sim \;{(dr)}^3$, и самодействие элемента $ dV$ есть $ G{(\rho dV)}^2/dr \sim {(dr)}^5 $, т.е. величина более высокого порядка, чем энергия взаимодействия с остальными массами, которая $ \sim {(dr)}^3$.

Используем теперь выражение $ \varphi$ для сферически-симметричного распределения $ \rho (r)$ и вычислим гравитационную энергию. Имеем:

$\displaystyle U={G\over 2}\int\limits_0^M dm \;\left\{-{m\over r}-\int\limits_r^R {dm (q\ )\over q}\right\}.$ (1.3)

Это выражение можно значительно упростить. Введем вспомогательную функцию 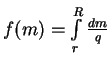$ f(m)=\int\limits_r^R {dm\over q}$. Очевидно,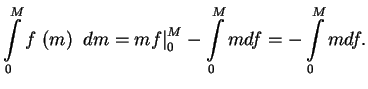 $ f(M)=0$ и кроме этого

$\displaystyle \int\limits_0^M f \;(m) \; \left. dm=mf \right\vert _0^M -\int\limits_0^M mdf=-\int\limits_0^M mdf. $

Имеем также $ df=-dm/q$.

Таким образом, интеграл от первого члена в выражении (1.3) равен интегралу от второго, и окончательно получим

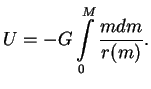
$\displaystyle U=-G\int\limits_0^M{mdm\over r(m)}. $

Это выражение проще получить иным путем, рассматривая, какую работу совершают гравитационные силы при наращивании данной конфигурации последовательными слоями. Пусть масса $ m$ с радиусом $ r$ уже изготовлена. Прибавим к этой массе новый сферический слой $ dm$. Тогда совершенная работа, очевидно, равна $ dU= {Gmdm\over r}$ и т.д. В результате получим

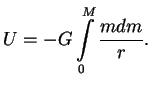
$\displaystyle U=-G\int\limits_0^M {mdm\over r}. $


<< 1.3 Сферически-симметричные поля тяг... | Оглавление | 1.5 Давление газа ... >>

Публикации с ключевыми словами: Эволюция звезд - внутреннее строение звезд - термоядерные реакции - физические процессы
Публикации со словами: Эволюция звезд - внутреннее строение звезд - термоядерные реакции - физические процессы
См. также:
Все публикации на ту же тему >>

Обсудить эту публикацию
Оценка: 3.0 [голосов: 119]
 
О рейтинге
Версия для печати Распечатать

Астрометрия - Астрономические инструменты - Астрономическое образование - Астрофизика - История астрономии - Космонавтика, исследование космоса - Любительская астрономия - Планеты и Солнечная система - Солнце

Астронет | Научная сеть | ГАИШ МГУ | Поиск по МГУ | О проекте | Авторам

Комментарии, вопросы? Пишите: info@astronet.ru или сюда

Rambler's Top100 Яндекс цитирования