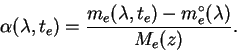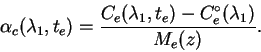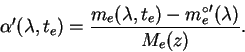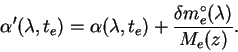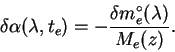Астронет > 6.6 Метод Никонова

по текстам по ключевым словам в глоссарии по сайтам перевод по каталогу

Прецизионная фотометрия

<< 6.5 Метод пары | Оглавление | 6.7 Метод Сарычева >>

6.6 Метод Никонова (метод контрольных звезд).

Метод В.Б.Никонова стал уже классическим. Он был предложен еще в сороковых годах. Владимир Борисович был поистине пионером отечественной фотоэлектрической фотометрии, и хотя его измерения 40-х и 50-х годов (как и измерения во всем мире!) велись в нестандартизованных фотометрических полосах и имеют в настоящее время в основном лишь исторический интерес, именно в процессе этих наблюдений родился знаменитый метод независимого определения изменяющихся коэффициентов экстинкции.

В методе Никонова мы должны выбрать и неоднократно измерять одну звезду, которую будем называть экстинкционной (или стандартной), а также измерять программные звезды. И это понятно! Ведь именно измерения программных звезд составляют цель любых наблюдений. Наша задача не только и не столько получить коэффициенты экстинкции, сколько определить внеатмосферные величины программных звезд.

Итак, в течение ночи мы многократно измеряем экстинкционную звезду и в промежутках между ее наблюдениями - программные звезды.

Если известны точные значения внеатмосферной звездной величины $m_e^\circ(\lambda)$ в монохроматическом свете с длиной волны $\lambda$ и показателя цвета $C_e^\circ(\lambda_1)$ экстинкционной звезды в данной инструментальной фотометрической системе (то есть разность монохроматических звездных величин для длин волн $\lambda$ и $\lambda_1$ ), то, пронаблюдав ее в момент времени , можно найти для этого момента

$\begin{displaymath} \alpha(\lambda,t_e)=\frac{m_e(\lambda,t_e)-m^{\circ}_e(\lambda)}{M_e(z)}. \end{displaymath}$

(6.25)

$\begin{displaymath} \alpha_c(\lambda_1,t_e)=\frac{C_e(\lambda_1,t_e)-C^{\circ}_e(\lambda_1)} {M_e(z)}. \end{displaymath}$

(6.26)

Интерполируя между значениями $\alpha$ и $\alpha_c$ , полученными в моменты

, и предполагая отсутствие азимутального эффекта, можем для любого момента найти $\alpha(\lambda,t)$ и $\alpha_c(\lambda_1,t)$ и далее

$\begin{displaymath} m_\circ(\lambda)=m(\lambda,t)-\alpha(\lambda,t)\,M(z), \end{displaymath}$

(6.27)

$\begin{displaymath} C_\circ(\lambda_1)=C(\lambda_1,t)-\alpha_c(\lambda_1,t)\,M(z). \end{displaymath}$

(6.28)

Пусть приближенное значение заатмосферной звездной величины экстинкционной звезды есть ${m_e^{\circ}}'(\lambda)$ . Его можно получить, например, производя вынос за атмосферу со средним для сезона значением коэффициента экстинкции. Тогда

(6.29)

где $m_e^{\circ}(\lambda)$ - истинная внеатмосферная величина экстинкционной звезды, а

- подлежащая определению поправка.

Пронаблюдав экстинкционную звезду в ряд моментов времени и получив наблюденные значения ее величины $m_e(\lambda,t_e)$ , находим предварительные значения мгновенных коэффициентов экстинкции

$\begin{displaymath} \alpha'(\lambda,t_e)=\frac{m_e(\lambda,t_e)-{m_e^\circ}'(\lambda)}{M_e(z)}. \end{displaymath}$

(6.30)

Подставляя в уравнение (6.30) формулы (6.25) и (6.29), имеем

$\begin{displaymath} \alpha'(\lambda,t_e)=\alpha(\lambda,t_e)+\frac{\delta m_e^\circ(\lambda)} {M_e(z)}. \end{displaymath}$

(6.31)

Итак, погрешность, внесенная в коэффициент экстинкции при использовании значения ${m_e^\circ}'(\lambda)$ , равна

$\begin{displaymath} \delta\alpha(\lambda,t_e)=-\frac{\delta m_e^\circ(\lambda)}{M_e(z)}. \end{displaymath}$

(6.32)

Теперь привлечем на помощь программные звезды. Очевидно, что для звезд постоянного блеска их внеатмосферные величины $m^\circ_{*}$ в разные моменты времени $t_{*}$ постоянны.

Измеренные величины программных звезд $m_{*}$ выносим за атмосферу с предварительными (неправильными) коэффициентами экстинкции $\alpha'$ проинтерполированными на моменты их наблюдений $t_{*}$ .

$\begin{displaymath} {m_{*}^\circ}'(\lambda)=m_{*}(\lambda,t_{*})-\alpha'(\lambda,t_{*})\,M_{*}(z). \end{displaymath}$

(6.33)

Подставляя (6.31) в (6.33), получаем

$\begin{displaymath} {m^\circ_{*}}'(\lambda)=m^\circ_{*}(\lambda)-\eta\,\delta m^\circ_e(\lambda), \end{displaymath}$

(6.34)

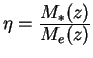где $\eta=\frac{\displaystyle M_{*}(z)}{\displaystyle M_e(z)}$ на момент $t_{*}$ .

Проводя повторные наблюдения программных звезд при различных значениях $\eta$ , можно найти, решая систему условных уравнений (6.34), неизвестную поправку $\delta m^\circ_e(\lambda)$ , а следовательно, согласно (6.29) и точное значение внеатмосферной величины экстинкционной звезды $m^\circ_e(\lambda)$ . Для показателей цвета совершенно аналогично

$\begin{displaymath} {C^\circ_{*}}'(\lambda_1)=C^\circ_{*}(\lambda_1,t)- \alpha'_c(\lambda_1,t-{*})\,M_{*}(z), \end{displaymath}$

(6.35)

$\begin{displaymath} {C^\circ_{*}}'(\lambda_1)=C^\circ_{*}(\lambda_1)- \eta\,\delta C^\circ_e(\lambda_1), \end{displaymath}$

(6.36)

где $\delta C^\circ_e(\lambda_1)$ - подлежащая определению поправка к предварительному внеатмосферному показателю цвета экстинкционной звезды.

Чем более различаются значения $\eta$ при повторных наблюдениях, тем увереннее определяются поправки $\delta m^\circ_e(\lambda)$ и $\delta C^\circ_e(\lambda_1)$ .

Теперь, когда определены внеатмосферные звездные величины и показатели цвета экстинкционной звезды

$\begin{displaymath} m^\circ_e(\lambda)= {m^\circ_e}'(\lambda) + \delta m^\circ_e(\lambda), \end{displaymath}$

(6.37)

$\begin{displaymath} C^\circ_e(\lambda_1)= {C^\circ_e}'(\lambda_1) + \delta C^\circ_e(\lambda_1), \end{displaymath}$

(6.38)

всю обработку наблюдений следует вести по формулам (6.27), (6.28) с истинными коэффициентами экстинкции, определяемыми согласно (6.25), (6.26).

Вся хитрость метода состоит в том, что Никонов привлек данные по программным звездам для определения поправки к коэффициенту экстинкции на момент наблюдения экстинкционной звезды.

Некоторые неудобства могут возникнуть в двух случаях. Во-первых, когда среди программных звезд много переменных, заметно изменяющих свой блеск в течение сеанса наблюдений. Во-вторых, когда программные звезды наблюдаются недалеко от зенита и разности воздушных масс $\Delta\eta$ при повторных наведениях на каждую из них близки к нулю.

Для исключения подобных неудобств в 1976 г. Никонов предложил модификацию своего метода, которую назвал методом контрольных звезд. В этой модификации роль программных звезд играют специально подобранные контрольные звезды, заведомо непеременные и удобно расположенные на небе. Контрольные звезды нужны еще и при обработке наблюдений в немонохроматических лучах (см. п.6.9).

<< 6.5 Метод пары | Оглавление | 6.7 Метод Сарычева >>

Публикации с ключевыми словами: Фотометрическая система - звездная величина - фотометрия - спектрофотометрия - атмосферное поглощение
Публикации со словами: Фотометрическая система - звездная величина - фотометрия - спектрофотометрия - атмосферное поглощение

См. также:

Звёздные величины

Заходящая тень Земли

Спектральное и фотометрическое исследование линзовидной галактики с оболочками NGC 474

Лаборатория исследования звездного магнетизма САО РАН

Лаборатория спектроскопии звезд САО РАН

Лаборатория спектроскопии и фотометрии внегалактических объектов САО РАН

Показатель цвета

Все публикации на ту же тему >>

Обсудить эту публикацию

Версия для печати

Астрометрия - Астрономические инструменты - Астрономическое образование - Астрофизика - История астрономии - Космонавтика, исследование космоса - Любительская астрономия - Планеты и Солнечная система - Солнце