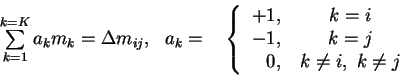Астронет > 5.7 Сеть вторичных стандартов

по текстам по ключевым словам в глоссарии по сайтам перевод по каталогу

Прецизионная фотометрия

<< 5.6 Тянь-Шаньская широкополосная ... | Оглавление | 6. Обработка измерений >>

5.7 О создании сети вторичных стандартов

Если в каждой спектральной полосе фотометрической системы заданы в качестве нуль-пункта внеатмосферные звездные величины одной избранной звезды (или суммы внеатмосферных звездных величин нескольких звезд), то говорят, что задан первичный стандарт системы. Со световым потоком от этой звезды -- первичного стандарта -- следует сравнивать потоки от всех других звезд, величины которых желательно определить в процессе наблюдений. Однако такое непосредственное сравнение далеко не всегда возможно. Для практических наблюдений необходимо иметь гораздо большее число звезд, для которых хорошо определены внеатмосферные звездные величины во всех полосах системы. Другими словами, для наблюдений нужно иметь сеть вторичных стандартов.

Звезды, составляющие сеть стандартов фотометрической системы, должны удовлетворять нескольким условиям.

Во-первых, они должны быть достаточно равномерно расположены на небесной сфере. Если сеть стандартов создается в сравнительно слабых (m6) звездных величинах, то это условие выполнить несложно. Желательно, чтобы звездные величины стандартов и программных звезд различались не более чем на 4-5 величин.

Во-вторых, для них желательно знать (хотя бы с не очень высокой точностью) распределение энергии в спектре $E(\lambda )$ или, по крайней мере, хорошо знать их спектральные типы и быть уверенным, что распределение энергии не имеет каких-либо экстравагантных особенностей (типа эмиссионных линий и т.п.). В случае необходимости можно пользоваться нормальным распределением энергии в спектре, принятым для данного спектрального типа (например из каталога Свидерскене). Если вы пользуетесь нормальным распределением энергии, то, в свою очередь, нужна уверенность, что межзвездное поглощение для этого стандарта практически отсутствует и не искажает вид функции $E(\lambda )$ . Желательно также, чтобы распределение энергии в спектре было достаточно гладкой функцией. В противном случае могут возникнуть сложности при применении тянь-шаньской методики учета экстинкции (см. гл. VI).

В третьих, стандарты должны быть проверены на переменность и необходима уверенность, что в пределах ошибок измерений нет переменности в используемых нами интервалах спектра.

На практике, процесс создания сети вторичных стандартов разбивается на несколько этапов.

На первом этапе вы, пользуясь всевозможными звездными каталогами, выбираете кандидатов в стандарты, по возможности равномерно расположенных на небе. При подборе следует пользоваться следующими критериями.

Среди кандидатов в стандарты должно быть достаточное количество звезд с наиболее гладкими распределениями энергии. Это звезды ранних спектральных классов. Обычно они выбираются из звезд главной последовательности в интервале спектральных классов B8-F5. Вместе с тем известно, что среди звезд этих спектральных классов нередко встречаются пульсирующие переменные типа $\delta$ Sct. Для этих звезд характерны амплитуды переменности $0{}^m\!\!\!.\,01$ - $0{}^m\!\!\!.\,1$ и периоды 0.003-0.02 суток. Открывать малоамплитудные переменные трудно, поэтому среди белых звезд еще очень много неоткрытых переменных типа $\delta$ Щита. Поэтому, среди кандидатов в стандарты должно быть также достаточно звезд главной последовательности спектральных классов F5-K0. В этом интервале спектров вероятность встретить переменность с малой амплитудой гораздо меньше. Большие же амплитуды открываются сравнительно просто, и среди достаточно ярких () звезд неизвестных переменных с амплитудами более $0{}^m\!\!\!.\,1$ должно быть немного.

Далее, необходимо тщательно проверить, нет ли в литературе указаний на переменность каждой из этих звезд. Прежде всего нужно проверить, не содержатся ли они звезд в ``Общем каталоге переменных звезд'' или в ``Новом каталоге звезд, заподозренных в переменности''.

На втором этапе нужно провести наблюдения этих кандидатов в стандарты. Поскольку звездные величины стандартов должны быть известны с максимально высокой точностью, нужно выбирать самые хорошие ночи с самой высокой стабильностью прозрачности. Обычно с вечера вы начинаете наблюдать какие-либо программные звезды, и, если убеждаетесь, что при близких воздушных массах измерения одного и того же объекта повторяются с разбросом, не превосходящим 1то следует перейти к наблюдениям стандартов. Тогда вы выбираете пару кандидатов в стандарты (с номерами и ) и ``привязываете'' их друг к другу, т.е. ведете наблюдения по схеме:

стандарт $i~\to$ фон у стандарта $i~\to$ стандарт $j \to$ фон у стандарта

Этот процесс следует повторить два-три раза. Вся серия измерений должна быть выполнена достаточно быстро, чтобы было основание пренебречь возможными небольшими изменениями атмосферной прозрачности и чувствительности приемной аппаратуры. Чтобы при обработке минимизировать ошибки выноса за атмосферу, наблюдения следует строить в соответствии с ``принципом равных высот'', т.е. оба стандарта пары, наблюдающейся в данный момент, должны находиться на близких зенитных расстояниях. Желательно, чтобы различие воздушных масс стандартов не превышало $0{}^m\!\!\!.\,05$ . В обсерваториях, находящихся выше $40^{\circ}$ северной широты, при привязке стандартов, имеющих отрицательные склонения, этому правилу не всегда легко следовать. Систематически нужно также привязывать вторичные стандарты к первичному.

Если вы ведете каталожные наблюдения, то можно производить привязки стандартов друг к другу одновременно с наблюдениями программных звезд. Для этого нужно наблюдать программные звезды не с одним, а с несколькими (двумя-четырьмя) стандартами и следить за тем, чтобы в разных сериях наблюдений состав такого набора частично изменялся. При этом трудно достичь строгого соблюдения требования равных высот, но при многочисленных наблюдениях можно получить достаточную точность. Преимущество данного способа в том, что вы можете наблюдать программные звезды до того, как будет полностью создана и увязана сеть вторичных стандартов. На практике применяют оба способа параллельно.

Когда накопится достаточное количество наблюдений разнообразных пар стандартов, можно приступать к третьему этапу: произвести наилучшим образом увязку измеренных разностей их звездных величин в единую систему.

После обработки равновысотных наблюдений и учета атмосферной экстинкции для каждой серии и для каждой фотометрической полосы получаются уравнения вида

$\begin{displaymath} m_i - m_j = \Delta m'_{ij} , \end{displaymath}$

(5.9)

где

-- соответственно, неизвестные внеатмосферные величины

-го и

-го стандартов в данной полосе, а $\Delta m'_{ij}$ -- измеренная разность этих величин в инструментальной системе.

Необходимо помнить, что сначала следует по формуле (5.8) перевести инструментальные разности $\Delta m'_{ij}$ в стандартные $\Delta m_{ij}$ .

Пусть у нас имеется различных стандартов, с номерами 1,2,3,..., каждый из которых сравнивался равновысотным методом по крайней мере с двумя другими стандартами. Некоторые из них сравнивались непосредственно с первичным стандартом, величины которого задают нуль-пункт фотометрической системы. Пусть, далее, мы выполнили серий равновысотных привязок пар стандартов. Тогда у нас есть условных уравнений типа (5.9) с неизвестными. Чтобы привести двучленные уравнения (5.9) к общему виду добавим в каждое из них члены с неизвестными звездными величинами всех остальных стандартов, но снабдим их нулевыми коэффициентами:

$\begin{displaymath} m_i-m_j=0\times m_1+0\times m_2+\cdots+1\times m_i+\cdots -1\times m_j+\cdots+0\times m_K=\Delta m_{ij}. \end{displaymath}$

Другими словами, трансформируем систему уравнений вида (5.9) к виду

$\begin{displaymath} \begin{array}{ll} \sum\limits_{k=1}^{k=K}a_km_k = \Delta m_{... ... $0$, & $k\neq i,\ k\neq j$\\ \end{tabular}\right. \end{array}\end{displaymath}$

(5.10)

Поскольку точность измерений для различных пар стандартов может быть различной, каждому уравнению (5.10) можно приписать вес. При назначении веса следует принимать во внимание различия в конкретных условиях наблюдений для каждой пары: среднюю воздушную массу и различие воздушных масс двух стандартов в момент наблюдений, угловое расстояние между стандартами, стабильность атмосферной прозрачности и так далее.

Система (5.10) является вырожденной. Определитель матрицы ее коэффициентов равен нулю. Чтобы решить эту систему, ее нужно дополнить еще одним уравнением. В нашем случае это уравнение, задающее нуль-пункт и аксиоматически присваивающее первичному стандарту значение его звездной величины.

$\begin{displaymath} m_{0}^{st} = {\textrm const} \end{displaymath}$

(5.11)

Систему (5.10) с дополнительным уравнением (5.11) можно решить способом наименьших квадратов.

При решении могут возникнуть вычислительные трудности, так как это довольно большая система. В обычных условиях бывает от нескольких десятков до нескольких сотен. -- несколько тысяч. Так, при создании сети стандартов фотометрической системы WBVR на первом этапе решалась система из 980 уравнений с 61 неизвестным, а на втором этапе -- из 4200 уравнений с 228 неизвестными.

В результате получаются увязанные внеатмосферные величины всех вторичных стандартов фотометрической системы.

<< 5.6 Тянь-Шаньская широкополосная ... | Оглавление | 6. Обработка измерений >>

Публикации с ключевыми словами: Фотометрическая система - звездная величина - фотометрия - спектрофотометрия - атмосферное поглощение
Публикации со словами: Фотометрическая система - звездная величина - фотометрия - спектрофотометрия - атмосферное поглощение

См. также:

Звёздные величины

Заходящая тень Земли

Спектральное и фотометрическое исследование линзовидной галактики с оболочками NGC 474

Лаборатория исследования звездного магнетизма САО РАН

Лаборатория спектроскопии звезд САО РАН

Лаборатория спектроскопии и фотометрии внегалактических объектов САО РАН

Показатель цвета

Все публикации на ту же тему >>

Обсудить эту публикацию

Версия для печати

Астрометрия - Астрономические инструменты - Астрономическое образование - Астрофизика - История астрономии - Космонавтика, исследование космоса - Любительская астрономия - Планеты и Солнечная система - Солнце