Rambler's Top100Astronet    
  по текстам   по ключевым словам   в глоссарии   по сайтам   перевод   по каталогу 		 

На первую страницу
Поверхностная фотометрия галактик
<< 3.1 Графические способы | Оглавление | 4. Стандартные модели галактик >>


3.2 Фотометрические параметры

Помимо перечисленных способов графического представления результатов, существует система стандартных параметров, определяемых по результатам поверхностной фотометрии, -- так называемая система параметров Вокулера (например, [59]).

$\bullet$ Система стандартных фотометрических параметров Вокулера

Основой этой системы параметров является понятие полной или асимптотической (или интегральной) видимой звездной величины объекта.

Рассмотрим галактику, имеющую круглые изофоты. Пусть $I(r)$ - поверхностная яркость на расстоянии $r$ от ее центра. Тогда светимость галактики в пределах $r$ от ядра: $L(\leq r)=\int_{0}^{2\pi}\int_{0}^{r}I(r)r{\rm d}\theta{\rm d}r=2\pi\int_{0}^{r}{\it I(r)r{\rm d}r}$. Полная (асимптотическая) светимость: $L_{T}=2\pi\int_{0}^{\infty}{\it I(r)r{\rm d}r}$.

Зная полную светимость галактики, можно ввести функцию $k(r)$, определяющую долю полной светимости, излучаемую в пределах расстояния $r$: $k(r)=L(\leq r)/L_{T}$. Часто рассматривают также зависимость доли полной светимости от изофоты -- $k(\mu)$. Графики зависимостей $k(r)$ и $k(\mu)$ называют кривыми относительной светимости.

Зависимости $k(r)$ и $k(\mu)$ определяют целое семейство параметров. Важнейший из них -- так называемый эффективный радиус $r_e$. Для галактики с круглыми изофотами $r_e$ -- это радиус круга, внутри которого излучается половина полной светимости, то есть $k(r_e)=1/2$. Эффективная поверхностная яркость $\mu_e$ - это поверхностная яркость на расстоянии $r_e$ от центра галактики или поверхностная яркость изофоты, для которой $k(\mu_e)=1/2$. Для галактики с эллиптическими изофотами вводится эффективная большая (малая) полуось $a_e$ ($b_e$) -- большая (малая) полуось изофоты, внутри которой излучается половина полной светимости галактики. Средняя поверхностная яркость внутри $\mu_e$ (или $r_e$): ${\langle I \rangle}_e=\frac{L_T}{2\pi r_e^2}$ или ${\langle \mu \rangle}_e=m_T+5\,{\rm lg}r_e+1.995$, где $m_T$ - полная видимая звездная величина галактики. К эффективному радиусу часто привязывают и измерения показателей цвета. Например, $(B-V)_e$ -- средний показатель цвета $B-V$ галактики в пределах эффективного радиуса (или в пределах эффективной диафрагмы $A_e$ -- см. далее).

Определив значение $r_e$, можно представить кривую относительной светимости в виде зависимости $m(\alpha)-m_T$ от lg$\alpha$, где $\alpha=r/r_e$, $m(\alpha)$ -- видимая звездная величина галактики в пределах безразмерного расстояния $\alpha$ от центра. Ее называют нормированной (нормализованной) кривой светимости. На практике кривая светимости часто строится по результатам многоапретурной фотометрии в пределах круглых диафрагм, центрированных на ядро галактики. В таком случае удобно рассматривать зависимость $m({\rm lg}A/A_e)$, где $A$ -- диаметр круглой диафрагмы, а $A_e$ -- диаметр эффективной диафрагмы, в пределах которой излучается половина полной светимости галактики. Удобство использования нормированных кривых состоит в том, что в такой форме можно сравнивать результаты наблюдений разных галактик.

Кроме эффективного радиуса $r_e$ вводятся также стандартные радиусы $r_1$ и $r_3$ такие, что $k(r_1)=$1/4 и $k(r_3)=$3/4. Через стандартные радиусы определяются индексы концентрации: $C_{21}=r_e/r_1$ и $C_{32}=r_3/r_e$. Индексы концентрации характеризуют глобальное распределение поверхностной яркости в галактике и коррелируют с ее морфологическим типом и отношением светимости балджа и диска [69,70] (см. далее п. 6.2). Существуют другие определения индекса концентрации -- например, в [71] на основе обобщенного фотометрического профиля (см. п. 3.1) вводится средний индекс концентрации. Близкий по смыслу индекс введен и в [72]. Индексы концентрации определяются гораздо проще, чем отношение светимостей балджа и диска, и они могут быть очень полезными при исследовании далеких слабых галактик [70,72,73].

Приведенные выше определения легко обобщаются на случай объекта с произвольными (не круглыми) изофотами путем замены $r$ на эквивалентный радиус $r^*$, равный радиусу круга, имеющего ту же площадь, что и данная изофота.

Полная видимая величина -- основа системы параметров Вокулера -- ищется экстраполяцией определяемых из наблюдений галактики зависимостей $m(A)$ или $m(r^*)$ (эти зависимости часто называют ``кривыми роста'' -- growth curves) на бесконечность [74,75]. Величина поправки при определении асимптотической звездной величины зависит от распределения поверхностной яркости в данной галактике. Конкретные значения этой поправки для галактик разных типов будут приведены далее в пп. 4- 6.

$\bullet$ Другие фотометрические параметры

Индекс вращательной асимметрии (например, [76,73,77]) определяется как
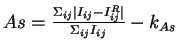$ As = \frac{\Sigma_{ij}\vert I_{ij}-I_{ij}^R\vert}{\Sigma_{ij}I_{ij}}-k_{As}$, где $I_{ij}$ -- поверхностная яркость элемента изображения с координатами ($i,~j$), $I_{ij}^R$ -- соответствующая поверхностная яркость после поворота изображения на 180$^{\rm o}$ относительно центра галактики. Слагаемое $k_{As}$ вводится для того, чтобы учесть вклад, вносимый шумом фона неба в изображение. На практике значение $k_{As}$ находится вычитанием из области изображения без объекта (фона) той же области, развернутой на 180$^{\rm o}$. При этом размеры областей с галактикой и с фоном должны совпадать. Существуют разные варианты этого индекса. Например, в [77] показано, что индекс, определяемый вычитанием исходного и развернутого на произвольный угол (а не только на 180$^{\rm o}$) изображений, также может быть полезным индикатором фотометрической структуры галактик.

Индекс асимметрии коррелирует с морфологическим типом и показателями цвета галактик [78,77]. Этот индекс очень полезен при автоматической массовой классификации (например, при изучении далеких объектов). В сочетании с индексом концентрации и показателями цвета он позволяет, например, ввести объективные количественные критерии для класса ``пекулярных'' галактик (например, [73,77]).

Несимметричность (``кривобокость'' -- lopsidedness) галактик характеризует отклонение их формы от круговой симметрии [79,80]. Этот параметр похож на параметр формы изофот (п. 3.1), но он не несет информации о форме галактики (дископодобной или ящикоподобной), а лишь отражает относительное смещение изофот от ее центра. Параметр несимметричности $A_1/A_0$ определяется как отношение амплитуд ряда Фурье с азимутальными числами $n=1$ и $n=0$, в который раскладывается наблюдаемое распределение яркости галактики на данном расстоянии от ядра (как правило, в интервале 1.5$h$-2.5$h$, где $h$ - это экспоненциальный масштаб ее диска).

В [80,81] показано, что $\sim20\%$ всех дисковых галактик демонстрируют азимутальную асимметрию распределения яркости (массы) с $\langle A_1/A_0 \rangle\geq$0.2. Причиной возникновения подобной несимметричной структуры звездных дисков галактик, возможно, является внешнее гравитационное возмущение или аккреция [80].

Наклон плоскости галактики к лучу зрения $i$ обычно оценивается по видимому сжатию галактики и может быть отнесен к фотометрическим параметрам. Согласно Хабблу [82], наклон сплюснутого сфероида с видимым сжатием $q=b/a$ и истинным сжатием $q_0$ может быть найден по формуле: ${\rm cos}^2i=(q^2-q_0^2)/(1-q_0^2)$. Наклон галактики также может быть оценен из сравнения эквивалентного профиля галактики и разреза вдоль ее большой оси [83], и из анализа индексов асимметрии [77].

К другим фотометрическим параметрам -- числам, характеризующим фотометрическую структуру галактики, -- можно отнести средние (или взвешенные по светимости средние) значения видимого сжатия (эллиптичности) галактики, $a_4/a$, позиционного угла изофот, параметра поворота изофот (то есть изменения позиционного угла большой оси изофот в пределах галактики) [84], радиус или диаметр, измеренные в пределах стандартной изофоты $\mu_B=25$ ($R_{25}$, $D_{25}$) и другие.


<< 3.1 Графические способы | Оглавление | 4. Стандартные модели галактик >>

Публикации с ключевыми словами: Фотометрическая система - слабые галактики - Скопление галактик - фотометрия
Публикации со словами: Фотометрическая система - слабые галактики - Скопление галактик - фотометрия
См. также:
Все публикации на ту же тему >>

Обсудить эту публикацию
Оценка: 3.1 [голосов: 81]
 
О рейтинге
Версия для печати Распечатать

Астрометрия - Астрономические инструменты - Астрономическое образование - Астрофизика - История астрономии - Космонавтика, исследование космоса - Любительская астрономия - Планеты и Солнечная система - Солнце

Астронет | Научная сеть | ГАИШ МГУ | Поиск по МГУ | О проекте | Авторам

Комментарии, вопросы? Пишите: info@astronet.ru или сюда

Rambler's Top100 Яндекс цитирования