| Предыдущая | Вверх | Следующая |
2.2 Системы отсчета в астрономии, видимое движение светил
- Пространственное расположение небесных тел, признание их движения, обращения Луны вокруг Земли, возможность математического расчета видимых положений планет.
- Мир ограничен сферой неподвижных звезд, сохранено равномерное движение планет, сохранены эпициклы, недостаточная точность предсказания положений планет.
- Необнаружение параллактического движения звезд в силу его малости и погрешностей наблюдений.
- Третьей координатой в сферической системе координат является модуль
радиуса-вектора - расстояние до объекта r. Эта координата определяется
из более сложных наблюдений, чем
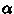 и
и 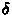 .
В каталогах ее эквивалентом является годичный параллакс, отсюда
.
В каталогах ее эквивалентом является годичный параллакс, отсюда 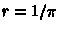 (пк). Для задач сферической астрономии достаточно знание только двух
координат
(пк). Для задач сферической астрономии достаточно знание только двух
координат 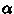 и
и 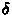 или альтернативных пар координат:
эклиптических -
или альтернативных пар координат:
эклиптических - 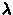 ,
, 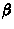 или галактических -
l, b.
или галактических -
l, b.
- Эклиптика, первый вертикал, колюры равноденствий и солнцестояний.
- На экваторе.
- Только большие круги небесной сферы проецируются в виде прямых линий.
- На полюсах Земли.
- Значения А, t,
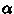 в этих случаях неопределенны.
в этих случаях неопределенны.
- На северном полюсе Земли, на экваторе, на южном полюсе Земли.
- 1) А=90o, z=do
2) А=270o, z=do
- а) На любой широте в любой момент видно половину небесной сферы;
б) на полюсах Земли видна, соответственно, северная и южная полусфера;
в) жа экваторе Земли за срок меньший года можно увидеть все звезды небесной сферы.
- На широтах
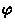 =-90o,
=-90o, 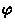 =+90o.
=+90o.
- На экваторе.
- На полюсах Земли.
- В верхней и нижней кульминациях.
- На земном экваторе для звезд с
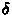 >0 А=0, а для звезд с
>0 А=0, а для звезд с
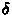 <0 А=180o.
<0 А=180o.
- В северном полушарии для всех звезд со склонением
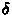 >
>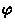 азимуты в верхней и нижней кульминациях одинаковы и равны 180o.
азимуты в верхней и нижней кульминациях одинаковы и равны 180o.
- Наблюдатель находится в одном из полюсов Земли или звезда находится в одном из полюсов мира.
- Быстрее всего в меридиане, медленнее всего в первом вертикале.
- Для наблюдателя, находящегося на земном экваторе и наблюдающего звезду
со склонением
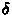 =0.
=0.
- Для всех широт - это звезда с
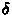 =0, на экваторе - любая
звезда.
=0, на экваторе - любая
звезда.
- Такое явление происходит на экваторе Земли со звездами, находящимися на небесном экваторе.
- На экваторе Земли.
- В дни равноденствий.
- В дни равноденствий на экваторе.
- В дни равноденствий суточная параллель Солнца совпадает с небесным экватором, являющимся большим кругом небесной сферы. В дни солнцестояний суточной параллелью Солнца является малый круг, отстоящий от небесного экватора на 23o.5.
- Если пренебречь изменением склонения Солнца в течение дня, то его восход был в точке востока. Это происходит ежегодно в дни равноденствий.
- Терминатор совпадает с земными меридианами в дни равноденствий.
- Кажущееся перемещение Солнца над горизонтом было истолковано как параллактическое смещение, а поэтому было использовано для попытки определения расстояния до светила.
- Искомое место находится на диаметрально противоположной точке земного
шара. Для Рязани эта точка - в южной части Тихого океана и имеет координаты
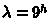 21m западной долготы и
21m западной долготы и 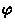 =-54o38'.
=-54o38'.
- Солнце находится в плоскости земной орбиты.
- Дважды в году во время дней равноденствий; один раз в году в дни солнцестояний.
- На экваторе сумерки самые короткие, так как Солнце поднимается и опускается перпендикулярно линии горизонта. В околополярных районах сумерки самые длинные, так как Солнце движется почти параллельно горизонту.
- Истинное солнечное время.
- Можно, но только для конкретной даты. Для разных видов времени должны быть свои циферблаты.
- Ритм жизни человека связан с Солнцем, а начало звездных суток попадает на разные часы солнечных суток.
- Сохранились бы звездный год и синодический месяц. Используя их, можно было бы ввести более мелкие единицы времени, а также построить календарь.
- Самые длинные истинные солнечные сутки бывают в дни солнцестояний,
когда скорость изменения прямого восхождения Солнца за счет его движения
по эклиптике наибольшая, причем в декабре сутки больше, чем в июне,
так как Земля в это время находится в перигелии.
Самые короткие сутки, очевидно, в дни равноденствий. В сентябре сутки короче, чем в марте, поскольку в это время Земля ближе к афелию.
- В этот период года склонение Солнца ежедневно увеличивается, и из-за разности в моментах наступления начала суток одной и той же даты для западных и восточных районов России долгота дня в Рязани 1 мая будет больше, чем в более восточных районах.
- Основная причина - связь общественной жизни со световым днем. Неодинаковость истинных солнечных суток ведет к появлению среднего солнечного времени. Зависимость среднего солнечного времени от долготы места обусловила изобретение поясного времени. Необходимость экономии электроэнергии привела к декретному и летнему времени.
- Солнечные сутки стали бы короче звездных на четыре минуты.
- Это происходит из-за заметного возрастания склонения Солнца в течение дня. Солнце после полудня описывает большую дугу на небосводе, чем до полудня.
- За счет рефракции. Солнце раньше восходит и позже заходит. Кроме того, в северном полушарии Земля летом проходит афелий и, следовательно, движется медленнее, чем зимой.
- Вследствие рефракции и наличия диска у Солнца день оказывается длиннее ночи.
- Это явление - следствие эллиптичности земной орбиты. Летом Земля находится в афелии и ее скорость по орбите меньше, чем скорость в зимние месяцы, когда Земля в перигелии.
- Безразлично.
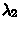 -
-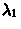 =Tm2-Tm1=S2-S1
=Tm2-Tm1=S2-S1
- Две.
| Предыдущая | Вверх | Следующая |
|
Публикации с ключевыми словами:
задачи - астрономическое образование
Публикации со словами: задачи - астрономическое образование | |
См. также:
Все публикации на ту же тему >> | |
Астрометрия
-
Астрономические инструменты
-
Астрономическое образование
-
Астрофизика
-
История астрономии
-
Космонавтика, исследование космоса
-
Любительская астрономия
-
Планеты и Солнечная система
-
Солнце