Колебания и волны. Лекции.
В.А.Алешкевич, Л.Г.Деденко, В.А.Караваев (Физический факультет МГУ)Издательство Физического факультета МГУ, 2001 г. Содержание
Рассуждения, приведенные выше, носят качественный характер. Для количественного описания нелинейного распространения волн мы используем наиболее упрощенный подход к анализу системы нелинейных уравнений (6.40) - (6.41). Оговоримся сразу, что поскольку уравнения Эйлера описывают поведение невязкой среды, то мы сможем проанализировать распространение волны лишь на первых двух этапах.
Перепишем уравнения в (6.41) в виде:
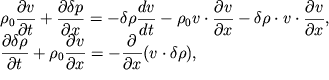 | (6.44) |
где все нелинейные члены, по порядку величины меньшие линейных, перенесены в правые части уравнений.
С учетом малости нелинейных членов для этих уравнений в нелинейной акустике
разработаны приближенные методы решения, смысл которых состоит в получении
значительно более простых уравнений, имеющих в ряде случаев несложные
аналитические решения. Одно из таких уравнений мы сейчас и получим, однако
сделаем это предельно просто. Для этого, во-первых, мы ограничимся вначале
лишь кинематической нелинейностью, а, во-вторых, будем предполагать, что
между скоростью ![]() и возмущением
и возмущением ![]() существует такая же связь,
как и в линейном режиме:
существует такая же связь,
как и в линейном режиме:
| (6.45) |
где ![]() - относительная деформация элементарного объема газа
(
- относительная деформация элементарного объема газа
(![]() при сжатии и
при сжатии и ![]() при разрежении). Эта связь
позволяет нам ограничиться одним из двух уравнений гидродинамики.
Предпочтительнее, например, воспользоваться более простым уравнением
непрерывности. При подстановке во второе уравнение (6.44) возмущения
плотности
при разрежении). Эта связь
позволяет нам ограничиться одним из двух уравнений гидродинамики.
Предпочтительнее, например, воспользоваться более простым уравнением
непрерывности. При подстановке во второе уравнение (6.44) возмущения
плотности ![]() пропорционального, согласно (6.45),
гидродинамической скорости v, получаем нелинейное уравнение:
пропорционального, согласно (6.45),
гидродинамической скорости v, получаем нелинейное уравнение:
| (6.46) |
Заметим, что в линейном режиме, когда правая часть уравнения равна нулю, его решением является любая функция вида:
| (6.47) |
описывающая бегущую со скоростью ![]() без искажения вдоль оси Ox
акустическую волну.
без искажения вдоль оси Ox
акустическую волну.
В нелинейном режиме ситуация усложняется. В самом деле, перепишем уравнение (6.46) в виде
| (6.48) |
Отсюда видно, что скорость участка волны равна
| (6.49) |
и зависит от гидродинамической скорости частиц.
Для фрагмента гармонической волны гидродинамической скорости, изображенного на рис. 6.10, это означает, что синусоидальное распределение скорости вдоль оси Ox трансформируется в пилообразное. Следовательно, оба механизма нелинейности способствуют трансформации гармонической волны в пилообразную.
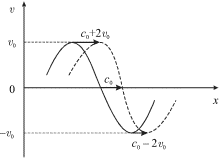 |
| Рис. 6.10. |
Если бы мы с самого начала учли действие обоих механизмов нелинейности, то из уравнений (6.44) и (6.40) мы бы получили уравнение
| (6.50) |
где ![]() - нелинейный параметр, отражающий действие
обоих механизмов нелинейности. Справедливости ради отметим, что формула
(6.49) не является точной, поскольку в отсутствие физической нелинейности
- нелинейный параметр, отражающий действие
обоих механизмов нелинейности. Справедливости ради отметим, что формула
(6.49) не является точной, поскольку в отсутствие физической нелинейности
![]() нелинейный параметр
нелинейный параметр ![]() и на самом деле
и на самом деле ![]() Это связано с тем, что мы использовали связь в виде (6.45), которая для
волн конечной амплитуды не является верной.
Это связано с тем, что мы использовали связь в виде (6.45), которая для
волн конечной амплитуды не является верной.
По аналогии с (6.47) мы можем записать решение уравнения (6.50) в виде:
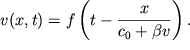 | (6.51) |
Это решение описывает эволюцию простых (Римановых) волн. Теперь не составляет труда количественно описать трансформацию гармонической волны в пилообразную.
Пусть на входе в среду (при ![]() )
)
| (6.52) |
Тогда на расстоянии ![]()
![$ v = v_{0} \sin {\displaystyle \left[ {\displaystyle \omega \left( {\displaystyle \tau + {\displaystyle \frac{\displaystyle {\displaystyle \beta }}{\displaystyle {\displaystyle c_{0}^{2} }}}x \cdot v} \right)} \right]}. $](http://images.astronet.ru/pubd/2002/04/09/0001175791/tex/formula1325.gif) | (6.53) |
Здесь ![]() - так называемое локальное время,
отсчитываемое наблюдателем, находящимся на расстоянии
- так называемое локальное время,
отсчитываемое наблюдателем, находящимся на расстоянии ![]() от начала координат,
от момента времени
от начала координат,
от момента времени ![]()
Для построения графика зависимости (6.53) перепишем ее в явном виде
| (6.54) |
где
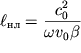 | (6.55) |
характерное расстояние, на котором развивается значительное нелинейное
искажение волны. Это расстояние сокращается с ростом амплитуды ![]() исходной волны и нелинейного параметра.
исходной волны и нелинейного параметра.
На рис. 6.11 изображены распределения скорости в пределах одного периода
колебаний для волны на расстояниях ![]() Из этих кривых видно, что синусоидальная волна
превращается постепенно в пилообразную, а при
Из этих кривых видно, что синусоидальная волна
превращается постепенно в пилообразную, а при ![]() в профиле
волны появляется неоднозначность. Эта неоднозначность не имеет физического
смысла и возникла лишь из-за пренебрежения вязкостью газа. В
действительности при
в профиле
волны появляется неоднозначность. Эта неоднозначность не имеет физического
смысла и возникла лишь из-за пренебрежения вязкостью газа. В
действительности при ![]() скорость испытывает скачок, или
разрыв (от величины скорости в точке А до величины скорости в точке В).
Положение ударного фронта задается линией АВ, которую проводят так, чтобы
заштрихованные площади сверху и снизу от АВ были бы одинаковы (в
рассматриваемом случае АВ совпадает с осью Oy). Таким построением
автоматически учитывается нелинейное затухание волны. Расстояние
скорость испытывает скачок, или
разрыв (от величины скорости в точке А до величины скорости в точке В).
Положение ударного фронта задается линией АВ, которую проводят так, чтобы
заштрихованные площади сверху и снизу от АВ были бы одинаковы (в
рассматриваемом случае АВ совпадает с осью Oy). Таким построением
автоматически учитывается нелинейное затухание волны. Расстояние ![]() как нетрудно теперь понять, является расстоянием, на котором у волны
появляются разрывы скорости
как нетрудно теперь понять, является расстоянием, на котором у волны
появляются разрывы скорости ![]() плотности
плотности ![]() и давления
и давления ![]() К
сожалению, без учета вязкости ширина ударного фронта получилась равной нулю.
В реальной ситуации она конечна и возрастает с увеличением вязкости.
К
сожалению, без учета вязкости ширина ударного фронта получилась равной нулю.
В реальной ситуации она конечна и возрастает с увеличением вязкости.
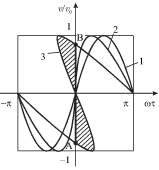 |
| Рис. 6.11. |
Учет вязкости позволяет описать III этап распространения, однако это выходит за рамки нашего курса.
Говоря об образовании ударного фронта в конце I этапа и последующем
нелинейном затухании на II этапе, мы не должны забывать о наличии обычного
(линейного) поглощения волны вследствие вязкости среды. Это поглощение
характеризуется коэффициентом ![]() (см. формулу (5.19)) и зависит от
частоты. Амплитуда волны при линейном поглощении уменьшается по
экспоненциальному закону уже на I этапе:
(см. формулу (5.19)) и зависит от
частоты. Амплитуда волны при линейном поглощении уменьшается по
экспоненциальному закону уже на I этапе: ![]() где
где ![]() характерное расстояние,
характеризующее поглощение звука. Естественно, что уменьшение амплитуды
характерное расстояние,
характеризующее поглощение звука. Естественно, что уменьшение амплитуды
![]() "притормаживает" процесс искажения профиля волны. Если поглощение
таково, что
"притормаживает" процесс искажения профиля волны. Если поглощение
таково, что ![]() то нелинейное искажение может и не
проявляться вовсе.
то нелинейное искажение может и не
проявляться вовсе.
В акустике отношение
| (6.56) |
называют акустическим числом Рейнольдса. Если ![]() то волна считается
мощной, и для нее имеет место нелинейное искажение. При
то волна считается
мощной, и для нее имеет место нелинейное искажение. При ![]() волна
слабая, и нелинейное искажение подавлено обычным линейным поглощением.
волна
слабая, и нелинейное искажение подавлено обычным линейным поглощением.
Если учесть далее, что амплитуда скорости ![]() связана с амплитудой
возмущения давления
связана с амплитудой
возмущения давления ![]() акустическим законом Ома, то
нелинейная длина будет обратно пропорциональна величине
акустическим законом Ома, то
нелинейная длина будет обратно пропорциональна величине ![]() :
:
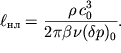 | (6.57) |
Следовательно, выражение для акустического числа Рейнольдса примет вид:
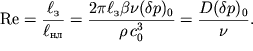 | (6.58) |
Здесь учтено, что в соответствии с формулой (5.21) ![]() - константа, характеризующая нелинейные и вязкостные
свойства среды.
- константа, характеризующая нелинейные и вязкостные
свойства среды.
|
Публикации с ключевыми словами:
колебания - волны
Публикации со словами: колебания - волны | |
|
См. также:
| |