Астронет > Механика твердого тела. Лекции.

по текстам по ключевым словам в глоссарии по сайтам перевод

Механика твердого тела. Лекции.

В.А.Алешкевич, Л.Г.Деденко, В.А.Караваев (Физический факультет МГУ)
Издательство Физического факультета МГУ, 1997 г. Содержание

Момент импульса твердого тела относительно оси. Момент инерции относительно оси.

В тех случаях, когда твердое тело вращается вокруг неподвижной оси, обычно оперируют с понятиями момента импульса и момента инерции относительно оси. Момент импульса $L_{\parallel}$ относительно оси - это проекция на данную ось момента импульса L, определенного относительно некоторой точки О, принадлежащей оси, причем, как оказывается, выбор точки О на оси значения не имеет.

Действительно, при вычислении $L_{\parallel}$ существенно лишь плечо импульса $\Delta {\displaystyle \bf p}_{i} = \Delta m_{i} {\displaystyle \bf v}_{i}$ относительно оси вращения O'O'' (рис. 2.12), то есть кратчайшее расстояние $\rho _{i}$ массы $\Delta m_{i}$ до оси:

$\left( {\displaystyle L_{i} } \right)_{\parallel} = \Delta m_{i} (r_{i} ^{2}v_{i} )_{{\displaystyle \parallel}} = \Delta m_{i} \rho _{i} v_{i} = (\Delta m_{i} \rho _{i}^{2} )\omega$

(2.31)

Здесь учтено, что скорость массы $\Delta m_{i}$ при вращательном движении $v_{i} = \omega \rho_{i} ; v_{i} \bot \rho_{i} .$

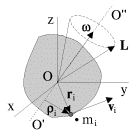Рис. 2.12.

Рассмотрим эту ситуацию более подробно. Пусть оси Ox, Oy, Oz на рис. 2.12 - главные оси инерции для точки O, O'O'' - неподвижная в лабораторной системе ось вращения, жестко связанная с телом. Вектор угловой скорости $\omega,$ направленный вдоль O'O'', можно разложить по осям системы координат xyz:

$\omega = {\displaystyle \left\{\displaystyle {\displaystyle \omega _{x} , \omega _{y} , \omega _{z} } \right\}} = {\displaystyle \left\{\displaystyle {\displaystyle \omega \cos \alpha , \omega cos\beta , \omega cos\gamma } \right\}},$

(2.32)

где $\cos \alpha , cos\beta , cos\gamma$ - направляющие косинусы оси O'O''. Вектор L не совпадает с $\omega$ и при вращении тела описывает коническую поверхность, симметричную относительно O'O''.Вектор L также можно разложить по осям системы xyz: ${\displaystyle \bf L} = {\displaystyle \left\{\displaystyle {\displaystyle L_{x} , L_{y} , L_{z} } \right\}},$ причем

$L_{x} = J_{x} \omega _{x} ; L_{y} = J_{y} \omega _{y} ; L_{z} = J_{z} \omega _{z} ,$

(2.33)

где $J_{x} , J_{y} , J_{z}$ - главные моменты инерции.

Проекция вектора L на ось вращения, или, что то же самое, момент импульса относительно оси

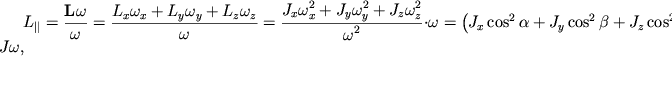$L_{\parallel} = {\displaystyle \frac{\displaystyle {\displaystyle {\displaystyle \bf L}\omega}}{\displaystyle {\displaystyle \omega }}} = {\displaystyle \frac{\displaystyle {\displaystyle L_{x} \omega _{x} + L_{y} \omega _{y} + L_{z} \omega _{z} }}{\displaystyle {\displaystyle \omega }}} = {\displaystyle \frac{\displaystyle {\displaystyle J_{x} \omega _{x}^{2} + J_{y} \omega _{y}^{2} + J_{z} \omega _{z}^{2} }}{\displaystyle {\displaystyle \omega ^{2}}}} \cdot \omega = \left( {\displaystyle J_{x} \cos ^{2}\alpha + J_{y} \cos ^{2}\beta + J_{z} \cos ^{2}\gamma } \right)\omega = J\omega ,$

(2.34)

где

$J = J_{x} \cos ^{2}\alpha + J_{y} \cos ^{2}\beta + J_{z} \cos ^{2}\gamma$

(2.35)

- момент инерции относительно оси.

Последняя формула позволяет рассчитать момент инерции твердого тела относительно произвольной оси в том случае, если известны главные моменты инерции $J_{x} , J_{y} , J_{z}$ и ориентация оси вращения относительно главных осей инерции (углы $\alpha , \beta , \gamma$ ). Во многих случаях такое вычисление оказывается значительно проще, чем прямое расчет по формуле

$J = {\displaystyle \sum\limits_{i} {\displaystyle \Delta m_{i} } }\rho _{i}^{2}$

(2.35)

(см. (2.31)).

Отметим, что, в соответствии с данным выше определением, $L_{\parallel}$ - величина скалярная (проекция вектора L на ось вращения). Вместе с тем можно говорить и о векторе ${\displaystyle \bf L}_{\parallel} ,$ рассматривая его как составляющую вектора L, вдоль оси:

$L_{\parallel} = {\displaystyle \sum\limits_{i} {\displaystyle \rho_{i} } }\times\Delta p_{i}$

(2.37)

(вектор $\rho_{i}$ изображен на рис. 2.12, $\Delta p_{i} = \Delta m_{i} v_{i}$ ). В рекомендуемых учебных пособиях можно встретить обе трактовки понятия момента импульса относительно оси.

Эллипсоид инерции.

Формула (2.35) для момента инерции относительно оси допускает наглядную геометрическую интерпретацию.

Представим, что через точку О начала координат системы xyz мы проводим прямые во всевозможных направлениях и на них откладываем отрезки длиной $R = {\displaystyle \frac{\displaystyle {\displaystyle k}}{\displaystyle {\displaystyle \sqrt {\displaystyle J} }}}$ (рис. 2.13), где $k$ есть постоянная величина, имеющая размерность кг^1/2*м². Геометрическим местом концов этих отрезков будет некоторая поверхность. Получим уравнение этой поверхности.

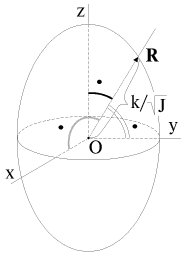Рис. 2.13.

Пусть оси Ox, Oy, Oz на рис. 2.13 - главные оси инерции. Проекции вектора R на оси координат составляют

$R_{x} \equiv x = R\cos \alpha = {\displaystyle \frac{\displaystyle {\displaystyle k}}{\displaystyle {\displaystyle \sqrt {\displaystyle J} }}}\cos \alpha ,$

(2.38)

$R_{y} \equiv y = R\cos \beta = {\displaystyle \frac{\displaystyle {\displaystyle k}}{\displaystyle {\displaystyle \sqrt {\displaystyle J} }}}\cos \beta ,$

(2.39)

$R_{z} \equiv z = R\cos \gamma = {\displaystyle \frac{\displaystyle {\displaystyle k}}{\displaystyle {\displaystyle \sqrt {\displaystyle J} }}}\cos \gamma ,$

(2.40)

откуда

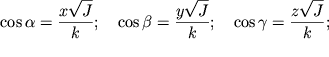$\cos \alpha = {\displaystyle \frac{\displaystyle {\displaystyle x\sqrt {\displaystyle J} }}{\displaystyle {\displaystyle k}}}; \quad \cos \beta = {\displaystyle \frac{\displaystyle {\displaystyle y\sqrt {\displaystyle J} }}{\displaystyle {\displaystyle k}}}; \quad \cos \gamma = {\displaystyle \frac{\displaystyle {\displaystyle z\sqrt {\displaystyle J} }}{\displaystyle {\displaystyle k}}};$

(2.41)

Подставляя (2.41) в (2.35), получим

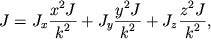$J = J_{x} {\displaystyle \frac{\displaystyle {\displaystyle x^{2}J}}{\displaystyle {\displaystyle k^{2}}}} + J_{y} {\displaystyle \frac{\displaystyle {\displaystyle y^{2}J}}{\displaystyle {\displaystyle k^{2}}}} + J_{z} {\displaystyle \frac{\displaystyle {\displaystyle z^{2}J}}{\displaystyle {\displaystyle k^{2}}}},$

(2.42)

или

$J_{x} \cdot x^{2} + J_{y} \cdot y^{2} + J_{z} \cdot z^{2} = k^{2}.$

(2.43)

Это, как известно, уравнение эллипсоида, который в данном случае называют эллипсоидом инерции.

Центр эллипсоида инерции, как видно из его уравнения, находится в начале координат системы xyz (точке О). Постоянная $k$ может быть выбрана произвольно и определяет масштаб построения; изменяя $k ,$ мы будем получать подобные эллипсоиды. Главные оси эллипсоида инерции являются главными осями инерции тела для точки О.

Эллипсоид инерции жестко связан с телом, а его положение относительно тела зависит от выбора точки О. Эллипсоид инерции, построенный для центра масс тела, называется центральным. Если известно положение эллипсоида инерции, известно и положение всего тела в данный момент времени. Рассматривая вращательное движение твердого тела, в ряде случаев можно абстрагироваться от его формы и иметь дело с эллипсоидом инерции. Для куба и шара, например, центральные эллипсоиды инерции вырождаются в сферу, поэтому эти тела с точки зрения многих задач механики оказываются эквивалентными.

Для примера рассмотрим сплошное однородный куб с ребром $a$ и массой $m$ . Эллипсоид инерции для центра одной из граней куба (точка О) показан на рис. 2.14. Полуоси OA, OB, OС лежат на главных осях инерции для точки О, причем ОА = ОB лежат в плоскости боковой грани, а $OC \approx 1,6 OA$ - перпендикулярна боковой грани. Для сравнения: эллипсоид инерции для центра куба вырождается в сферу с радиусом, равным ОС.

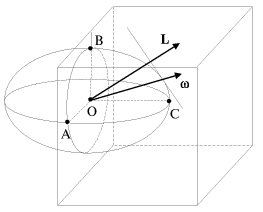Рис. 2.14.

Понятие эллипсоида инерции позволяет с помощью достаточно простого графического построения установить связь между угловой скоростью $\omega$ и моментом импульса L относительно точки О, принадлежащей оси вращения. Речь идет о так называемом построении Пуансо, которое мы приводим без доказательства: необходимо построить эллипсоид инерции с центром в точке О и в точке его пересечения с осью вращения (вектором угловой скорости $\omega$ ) ( провести плоскость, касательную к эллипсоиду. Перпендикуляр, опущенный из центра эллипсоида инерции на касательную плоскость, и даст направление вектора момента импульса L Пример подобного построения представлен на обсуждавшемся выше рис. 2.14.

Назад| Вперед

Публикации с ключевыми словами: механика - твердое тело - углы Эйлера Публикации со словами: механика - твердое тело - углы Эйлера
См. также: Механика сплошных сред Вариационные принципы механики Анизотропия

Мнение читателя [1]

Версия для печати

Астрометрия - Астрономические инструменты - Астрономическое образование - Астрофизика - История астрономии - Космонавтика, исследование космоса - Любительская астрономия - Планеты и Солнечная система - Солнце