Механика твердого тела. Лекции.
В.А.Алешкевич, Л.Г.Деденко, В.А.Караваев (Физический факультет МГУ)Издательство Физического факультета МГУ, 1997 г. Содержание
Кинетическая энергия при плоском движении.
Кинетическая энергия твердого тела представляет собой сумму кинетических энергий отдельных частиц:
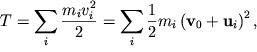 | (3.37) |
где ![]() - скорость центра масс тела,
- скорость центра масс тела, ![]() - скорость
i-й частицы относительно системы координат, связанной с центром масс и
совершающей поступательное движение вместе с ним. Возводя сумму скоростей в
квадрат, получим:
- скорость
i-й частицы относительно системы координат, связанной с центром масс и
совершающей поступательное движение вместе с ним. Возводя сумму скоростей в
квадрат, получим:
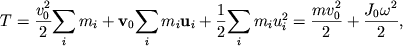 | (3.38) |
так как ![]() (суммарный импульс
частиц в системе центра масс равен нулю).
(суммарный импульс
частиц в системе центра масс равен нулю).
Таким образом, кинетическая энергия при плоском движении равна сумме кинетических энергий поступательного и вращательного движений (теорема Кенига). Если рассматривать плоское движение как вращение вокруг мгновенной оси, то кинетическая энергия тела есть энергия вращательного движения.
В этой связи задачу о скатывании цилиндра с наклонной плоскости можно решить, используя закон сохранения механической энергии (напомним, что сила трения при качении без проскальзывания работу не совершает).
Приращение кинетической энергии цилиндра равно убыли его потенциальное энергии:
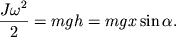 | (3.39) |
Здесь ![]() - длина наклонной плоскости,
- длина наклонной плоскости, ![]() - момент
инерции цилиндра относительно мгновенной оси вращения.
- момент
инерции цилиндра относительно мгновенной оси вращения.
Поскольку скорость оси цилиндра ![]() то
то
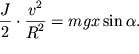 | (3.40) |
Дифференцируя обе части этого уравнения по времени, получим
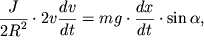 | (3.41) |
откуда для линейного ускорения ![]() оси цилиндра будем
иметь то же выражение, что и при чисто динамическом способе решения (см.
(3.27, 3.36)).
оси цилиндра будем
иметь то же выражение, что и при чисто динамическом способе решения (см.
(3.27, 3.36)).
Замечание. Если цилиндр катится с проскальзыванием, то изменение его кинетической энергии будет определяться также и работой сил трения. Последняя, в отличие от случая, когда тело скользит по шероховатой поверхности, не вращаясь, определяется, в соответствии с (3.14), полным углом поворота цилиндра, а не расстоянием, на которое переместилась его ось.
III. Движение аксиально симметричного твердого тела, закрепленного в центре масс.
Такое движение можно реализовать с помощью специального устройства, называемого кардановым подвесом (рис. 3.13). Положение тела в подвесе должно быть таким, чтобы оси AA', BB' и CC' пересекались в центре масс. В этом случае при любых возможных движениях тела его центр масс остается неподвижным. При этом ось AA' (в данном случае - ось симметрии тела) может занимать произвольную ориентацию в пространстве.
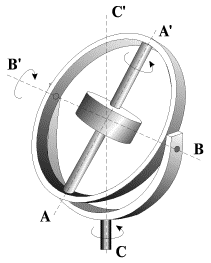 |
| Рис. 3.13. |
Задачей о движении твердого тела, закрепленного в точке, занимались многие ученые: Л. Эйлер, большая часть жизни которого была связана с Петербургской Академией Наук, выдающиеся русские ученые Н. Е. .Жуковские, С. В. Ковалевская, С. А. Чаплыгин, французские ученые Ж. Лагранж, С. Пуассон, Л. Пуансо. Оказалось, что в общем случае эта задача аналитически неразрешима. Даже в простейшем случае движения твердого тела только под действием силы тяжести точное решение существует лишь в особых частных случаях. Один из этих случаев, когда однородное тело вращения закреплено в центре масс, мы рассмотрим в этой лекции, другой, имеющий отношение к движению гироскопа, - в лекции 4.
Уравнения Эйлера.
Рассмотрим однородное аксиально симметричное тело вращения, закрепленное в центре масс О (рис. 3.14). Центральный эллипсоид инерции такого тела является эллипсоидом вращения с осью симметрии Oz.
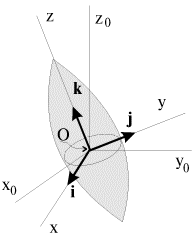 |
| Рис. 3.14. |
Система координат x0y0z0 на рис. 3.14 - лабораторная,
система xyz жестко связана с телом, причем оси Ox, Oy и Oz - главные
центральные оси инерции тела. Поскольку это тело вращения, то главные осевые
моменты инерции ![]() и
и ![]() равны между собой:
равны между собой: ![]()
Суммарный момент сил тяжести относительно точки закрепления (центра масс) равен нулю, иных сил, кроме сил тяжести, нет, поэтому уравнение моментов (3.2) имеет вид
| (3.42) |
откуда
| (3.43) |
то есть момент импульса раскрученного и предоставленного самому себе тела остается постоянным по величине и направлению.
Замечание. Если исследуемое тело - шар, то ![]() и центральный эллипсоид инерции трансформируется в сферу. Это означает. что
любая центральная ось вращения является главной осью инерции шара, то есть
имеет место простое соотношение
и центральный эллипсоид инерции трансформируется в сферу. Это означает. что
любая центральная ось вращения является главной осью инерции шара, то есть
имеет место простое соотношение ![]() где
где ![]() - момент инерции
относительно центральной оси, и при
- момент инерции
относительно центральной оси, и при ![]() получаем
получаем ![]() Ось вращения совпадает по направлению с L и сохраняет свою ориентацию
в пространстве.
Ось вращения совпадает по направлению с L и сохраняет свою ориентацию
в пространстве.
Теперь допустим, что ![]() отлично от
отлично от ![]() и
и ![]() как, например,
на рис. 3.14. В этом случае чистое вращение имеет место только тогда, когда
ось вращения либо совпадает с осью симметрии тела, либо перпендикулярна к
ней.
как, например,
на рис. 3.14. В этом случае чистое вращение имеет место только тогда, когда
ось вращения либо совпадает с осью симметрии тела, либо перпендикулярна к
ней.
Общий случай более сложен; обычно его рассматривают с помощью дифференциальных уравнений Эйлера. Дело заключается в том, что если в уравнении (3.42) вектор L спроектировать на оси лабораторной системы x0y0z0, то скалярные дифференциальные уравнения движения будут весьма сложными, поскольку моменты инерции относительно неподвижных осей будут функциями времени. Поэтому гораздо удобнее рассматривать L, в проекциях на оси системы xyz, жестко связанной с твердым телом.
Пусть i, j, k - единичные орты системы xyz, жестко связанной с твердым телом (рис. 3.14). Тогда (3.42) принимает вид
| (3.44) |
где не только проекции ![]() но и единичные орты i, j, k являются функциями времени. Поэтому из (3.44) следует
но и единичные орты i, j, k являются функциями времени. Поэтому из (3.44) следует
| (3.45) |
Здесь использован символ ![]() чтобы подчеркнуть, что рассматриваются изменения во времени проекций
чтобы подчеркнуть, что рассматриваются изменения во времени проекций
![]() и
и ![]() относительно подвижной системы xyz - системы,
которая, в свою очередь, поворачивается вместе с телом с мгновенной угловой
скоростью
относительно подвижной системы xyz - системы,
которая, в свою очередь, поворачивается вместе с телом с мгновенной угловой
скоростью ![]()
Что касается производных по времени от единичных ортов i, j,
k , то их изменения во времени обусловлены только вращением системы
xyz с угловой скоростью ![]() поэтому
поэтому
| (3.46) |
(см. рис. 3.15). Подставляя эти выражения в (3.45), получим:
| (3.47) |
Преобразование
| (3.48) |
находится в полной аналогии с преобразованием скорости при переходе от
неподвижной к вращающейся системе координат. Существенно, что наблюдатель,
находящийся в системе xyz, фиксирует только относительное изменение L
(член ![]() ).Для наблюдателя в лабораторной системе к относительному изменению L
добавляется его "переносное" изменение, связанное с вращением системы xyz с
мгновенной угловой скоростью
).Для наблюдателя в лабораторной системе к относительному изменению L
добавляется его "переносное" изменение, связанное с вращением системы xyz с
мгновенной угловой скоростью ![]()
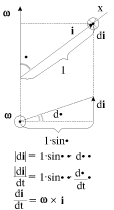 |
| Рис. 3.15. |
|
Публикации с ключевыми словами:
механика - твердое тело - углы Эйлера
Публикации со словами: механика - твердое тело - углы Эйлера | |
|
См. также:
| |