по текстам   по ключевым словам   в глоссарии   по сайтам   перевод

ЧЕТВЕРТАЯ ВСЕРОССИЙСКАЯ ОТКРЫТАЯ ЗАОЧНАЯ
ШКОЛЬНАЯ АСТРОНОМИЧЕСКАЯ ОЛИМПИАДА
ЗАДАЧИ С РЕШЕНИЯМИ

1. Условие. Искусственный спутник Земли обращается вокруг нашей планеты по круговой орбите, лежащей в плоскости эклиптики. При наблюдении из Краснодара этот спутник и точка весеннего равноденствия всегда восходят над горизонтом строго одновременно. В определенные моменты времени спутник оказывается на небе точно над точкой юга. На какой высоте над горизонтом он в это время находится? Чему равен радиус орбиты спутника? Рефракцией и суточным параллаксом спутника пренебречь.

 

1. Решение. В любом месте Земли, кроме полюсов, точка весеннего равноденствия восходит ровно через одни звездные сутки (около 23 часов 56 минут) после предыдущего восхода. Следовательно, восходы искусственного спутника также отстоят друг от друга на одни звездные сутки. Так как мы не учитываем суточное параллактическое смещение спутника, он всегда будет находиться на эклиптике. На широте Краснодара (+45?) эклиптика не может совпадать с горизонтом и, являясь большим кругом небесной сферы, пересекает горизонт в двух противоположных точках. Одна из них - восходящая в этот момент точка весеннего равноденствия, вторая - точка осеннего равноденствия. Таким образом, в момент своего восхода искусственный спутник Земли находился в одной из этих двух точек. По прошествии одних звездных суток спутник будет восходить в той же точке неба. В противоположной точке круговой орбиты он бы не восходил, а заходил за горизонт, так как в любой момент времени над горизонтом располагается ровно половина орбиты спутника.

Очевидно, что спутник, вращаясь вокруг Земли, не может быть неподвижным относительно звезд. Рассмотрим случаи, при которых искусственный спутник Земли, один раз восходя и заходя за горизонт, возвращается в ту же точку неба по прошествии звездных суток. Это, в частности, может быть, если период обращения спутника равен звездным суткам, а направление совпадает с направлением вращения Земли. Такая орбита похожа на геостационарную, но так как спутник вращается не в плоскости экватора, а в плоскости эклиптики, на земном небе он будет описывать узкую <восьмерку> размером около 47?. Если при этом он окажется в точке весеннего равноденствия в момент ее восхода, то он и сам будет восходить в это же время на востоке каждые звездные сутки (см. рисунок).

 

 

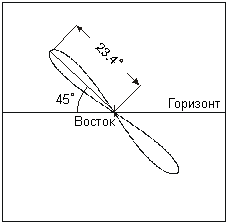
Однако данная картина противоречит условию задачи - из рисунка можно убедиться, что спутник всегда будет находиться в восточной части неба и никогда не окажется над южным горизонтом. Нам необходимо рассмотреть еще один возможный вариант, при котором спутник за одни сутки завершает оборот по небу относительно земного наблюдателя, один раз восходя и заходя за горизонт. Обозначим синодический период обращения спутника через S, сидерический (звездный) период его обращения через T, а продолжительность звездных суток через T₀. Эти три величины связаны соотношением

 

 

Знак <+> перед величинами (1/S) и (1/T) соответствует вращению спутника относительно наблюдателя и относительно центра Земли в направлении, совпадающем с направлением вращения Земли, а знак <-> соответствует противоположному направлению. Так как величины S и T₀ равны друг другу, знак <-> перед величиной (1/S) стоять не может, иначе величина T обратится в бесконечность. Так как величина S положительна, решение будет существовать только при одной комбинации знаков:

 

 

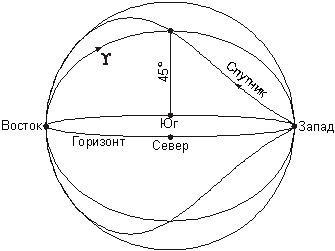
из чего мы получаем, что сидерический период обращения спутника T равен половине звездных суток, то есть 11 часам 58 минутам. Спутник вращается в одном направлении с Землей, но с вдвое большей угловой скоростью, поэтому он, как Фобос на Марсе, будет восходить на западе и заходить на востоке. Во время своего восхода спутник будет находиться в точке осеннего равноденствия, которая сама при этом будет заходить за горизонт. Перемещаясь с запада на восток, спутник будет двигаться навстречу точке весеннего равноденствия, взошедшей одновременно с ним в противоположной точке неба (см. второй рисунок). Через 5 часов 59 минут после восхода спутник сделает половину сидерического оборота вокруг Земли и окажется в точке весеннего равноденствия, которая при этом будет кульминировать над южным горизонтом на высоте 45?. Мы получили ответ на первый вопрос задачи.

 

 

Для ответа на второй вопрос достаточно воспользоваться обобщенным III законом Кеплера. Радиус орбиты равен

 

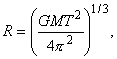
что составляет 26.6 тысяч километров (M - масса Земли).

 

 

2. Условие. Искусственный спутник Земли обращается вокруг нашей планеты по эллиптической орбите, лежащей в плоскости эклиптики. В перигее он находится на том же расстоянии от Земли, что и Луна. Оцените максимально возможный эксцентриситет орбиты спутника. Гравитационное влияние Луны не учитывать.

 

2. Решение. Возможное значение эксцентриситета орбиты спутника ограничено сверху приливным влиянием Солнца (влияние Луны, по условию задачи, в расчет не берется). Если в точке апогея орбиты спутник подойдет к внутренней точке Лагранжа системы Солнце-Земля, орбита спутника станет неустойчивой, и он перейдет на гелиоцентрическую орбиту, став искусственной планетой Солнечной системы. Рассмотрим наиболее критический для устойчивости орбиты случай, когда в апогее спутник оказывается между Солнцем и Землей (см. рисунок). Так как орбита спутника лежит в плоскости эклиптики, то подобная ситуация обязательно реализуется один раз в год.

 

 

Обозначим перигейное и апогейное расстояние до спутника соответственно как p и a, расстояние от Солнца до Земли - через R. Предположим, что в точке апогея спутник оказался во внутренней точке Лагранжа. Эта точка может двигаться вокруг Солнца с той же угловой скоростью w, что и Земля. Запишем уравнения вращения точки Лагранжа и Земли:

 

 

Учитывая, что величина a значительно меньше, чем R, можно записать

 

 

Выражая величину w из уравнения вращения Земли, получаем

 

 

Из последнего соотношения получаем оценку максимального значения апогейного расстояния

 

 

и эксцентриситета орбиты спутника (с учетом известного значения p, равного 384 тысячам километров):

 

 

 

 

Эксцентриситет при этом получается равным 0.633. Учитывая оценочный характер задачи, такой подход вполне логичен и при правильных вычислениях вполне может быть оценен в 6 баллов. Остальные подходы оцениваются меньшим количеством баллов в зависимости от их правдоподобности.

 

3. Условие. Далекая звезда находится на небе в точке летнего солнцестояния. Во время прохождения мимо звезды восходящего узла лунной орбиты на Земле в каждый оборот Луны будет наблюдаться покрытие данной звезды Луной. Сколько покрытий будет содержать серия? На какой широте и в какой части неба будет видно первое и последнее покрытие звезды Луной в серии? Орбиту Луны считать круговой.

 

3. Решение. Если бы Луна обращалась вокруг Земли точно в плоскости эклиптики, то она покрывала бы звезду в точке летнего солнцестояния в свой каждый оборот вокруг Земли, причем это покрытие было бы видно в экваториальном и северном тропическом поясах нашей планеты. На самом деле плоскость орбиты Луны наклонена к плоскости эклиптики на угол i, равный 5.15?, что оказывается достаточным для того, чтобы в большинстве случаев Луна прошла на небе выше или ниже звезды, и покрытие не наступило. Для того, чтобы оно все же случилось, Луна, проходя на небе мимо звезды, должна находиться вблизи одного из двух узлов своей орбиты, в которых она пересекает плоскость эклиптики.

Сидерический (звездный) период обращения Луны T_S составляет 27.321662 суток, а драконический период T_D (период возвращения к тому же узлу орбиты) немного короче - 27.212220 суток. Завершая свой оборот относительно звезд, Луна совершит 1.00402 драконических оборота, и если одно покрытие произошло точно в восходящем узле лунной орбиты, то следующее произойдет уже после прохождения этого узла, при этом Луна окажется чуть выше, и область видимости покрытия на Земле сместится на север (см. рисунок).

 

 

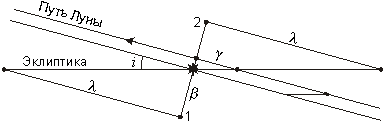
Угловое расстояние между Луной и узлом орбиты составит

 

 

Смещаясь на такую величину каждый сидерический месяц, линия узлов лунной орбиты сделает полный оборот за 248.65 сидерических месяцев, то есть за 18.6 лет. За этот период наступят две эпохи покрытий Луной звезды вблизи эклиптики - во время прохождения восходящего и нисходящего узла орбиты вблизи звезды. Для звезды, находящейся точно на эклиптике, эти серии будут отстоять на 9.3 года друг от друга. В задаче требуется найти продолжительность одной серии. Для этого нужно определить, на каком максимальном удалении от узла орбиты Луны может произойти покрытие.

 

 

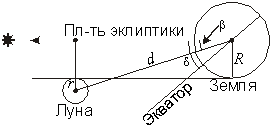
На втором рисунке показана предельная ситуация, при которой касательное покрытие звезды Луной видно только в одной точке Земли. Максимальное угловое расстояние Луны от эклиптики в этом случае составляет

 

 

Здесь, по условию задачи, мы принимаем орбиту Луны круговой с радиусом d, равному 384.4 тысяч км, R и r - радиусы Земли и Луны. Возвращаясь к первому рисунку, вычисляем максимальное расстояние от Луны до узла орбиты во время покрытия:

 

l=bctg i=13.41?.

 

Среднее количество покрытий в одной серии, как видно из первого рисунка, будет равно

 

 

Реальное число покрытий примерно с одинаковой вероятностью будет равно 18 или 19. Продолжительность серии составит 17 или 18 сидерических периодов обращения Луны, то есть 1.27 или 1.35 года.

Первое покрытие звезды Луной в случае восходящего узла произойдет вблизи положения 1 на первом рисунке, та же ситуация изображена на втором рисунке. Луна заденет звезду своим северным краем, и это покрытие будет видно в южном полушарии Земли. Луна будет находиться на северном горизонте (точнее, в 5.15? вдоль горизонта к западу от точки севера), склонение звезды d составляет +23.4?, и покрытие будет наблюдаться вблизи Южного Полярного Круга. Последнее покрытие серии (положение 2 на первом рисунке) будет видно вблизи Северного Полярного Круга в 5.15? к востоку от точки севера вдоль горизонта.

 

 

4. Условие. Полоса видимости полного солнечного затмения прошла поочередно по городам: Осло (Норвегия), Варшава (Польша), Констанца (Румыния), Анкара (Турция), Багдад (Ирак), Керман (Иран) и Исламабад (Пакистан). В каком из четырех астрономических сезонов года произошло данное затмение?

 

4. Решение. В таблице приведены координаты перечисленных в условии городов.

 

 

Из таблицы видно, что тень большую часть времени двигалась на юго-восток, и лишь в конце она стала двигаться на восток, а затем даже повернула к северо-востоку. Видимый путь тени по поверхности Земли показан на карте.

 

 

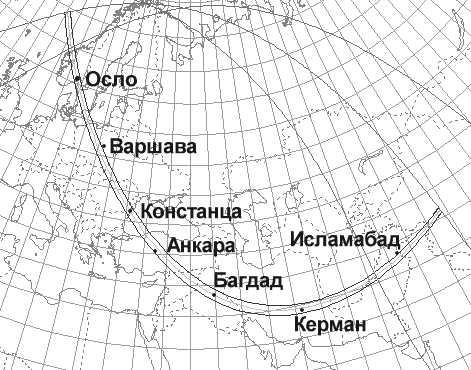
Рассмотрим, как могла бы двигаться тень Луны по умеренным и тропическим широтам северного полушария в середине четырех астрономических сезонов года (напоминаем, что началом сезона считается момент равноденствия или солнцестояния). На рисунке для каждого из четырех случаев показан вид Земли и полосы тени со стороны Солнца и Луны. Лунная тень движется на рисунке слева направо, в направлении, противоположном направлению движения Земли по орбите (на самом деле, она образует с этим направлением угол 5.15?, но это не изменяет решения задачи, так как данный угол существенно меньше угла наклона земного экватора к эклиптике).

 

 

На втором рисунке мы видим, что подобным образом тень может двигаться по Земле только астрономической осенью, то есть в промежутке между осенним равноденствием и зимним солнцестоянием.

Данная задача имеет реальный прототип - полное солнечное затмение 19 ноября 1816 года, карта которого приведена выше. Полоса полной фазы тогда прошла через центр или пригороды всех семи городов, приведенных в условии задачи.

 

 

5. Условие. Значения астрономического азимута восхода и последующего захода некоторой планеты в Санкт-Петербурге составили соответственно -90.0? и +90.4?. Заход диска планеты за горизонт длился 3.2 секунды. Что это за планета, и можно ли что-то сказать о времени года, когда это произошло?

 

5. Решение. Значения азимутов точек восхода и захода указывает на то, что планета находилась вблизи небесного экватора. Так как планеты располагаются на небе вблизи эклиптики, значит, это была окрестность точки весеннего или осеннего равноденствия. Между восходом и заходом планеты прошло примерно 12 часов. Азимут точки захода по модулю на 0.4? превосходит азимут точки восхода, то есть за эти 12 часов склонение планеты увеличилось. Определим, насколько оно увеличилось.

 

 

Из рисунка видно, что изменение модуля азимута восхода и захода DA связано с изменением склонения объекта Dd и широтой места наблюдения j (равной +60?) соотношением:

 

Dd=DAcosj=+0.2?.

 

Учет атмосферной рефракции не изменит этот результат, так как вблизи небесного экватора рефракция изменяет значения азимутов восхода и захода, но практически не изменяет их разность DA. Далее заметим, что планета движется среди звезд вдоль эклиптики - это справедливо всегда, кроме моментов стояний планет, но тогда их угловая скорость очень маленькая. Вблизи точек равноденствия эклиптика проходит под углом e=23.4? к небесным параллелям (и экватору), и полное угловое перемещение планеты среди звезд за 12 часов составит

 

 

В итоге, угловая скорость планеты составляет 1?/сутки, что практически совпадает с угловой скоростью движения Солнца по небу. Ни одна планета не может достичь такой угловой скорости во время попятного движения, да и прямым движением с такой скоростью могут перемещаться только две внутренние планеты, Меркурий и Венера, во время эпохи максимального углового расстояния от Солнца.

Для того чтобы определить, какая именно эта планета, определим ее видимые размеры. Известно, что продолжительность захода диска планеты за горизонт Dt составила 3.2 секунды. Находясь вблизи небесного экватора, планета переместилась за это время относительно земного наблюдателя на угловое расстояние l, равное

 

l=15²Dt=48².

 

Угловой диаметр планеты составляет

 

d=2r=lcosj=24².

 

Полученное значение совпадает с угловыми размерами диска Венеры во время ее наибольшей элонгации (видимый размер Меркурия в это время не превышает 8²). Планета находится в наибольшей элонгации, в 47? от Солнца и, двигаясь в прямом направлении, проходит точку весеннего равноденствия. Если это наибольшая восточная элонгация, то картина наблюдалась в начале февраля, если наибольшая западная элонгация - в начале мая.

 

 

6. Условие. Находясь в точке наибольшей восточной элонгации, Меркурий вступил в соединение с Венерой, более чем в 5 раз уступая ей по видимому диаметру. У какой из планет ближайшее нижнее соединение с Солнцем произойдет раньше? На сколько времени? Орбиты Меркурия, Венеры и Земли считать круговыми.

 

6. Решение. Положение Меркурия, Венеры и Земли в указанный в условии момент показано на рисунке.

 

 

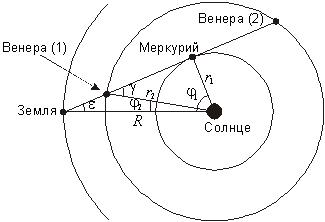
Находясь в соединении с Меркурием, Венера может находиться в двух точках своей орбиты, помеченных на рисунках цифрами 1 и 2. Но, как уже было отмечено в решении предыдущей задачи, угловой диаметр Меркурия в момент наибольшей элонгации составляет около 8², следовательно, угловой диаметр Венеры превышает 40². Такое может быть, только если Венера находится в положении 1, недалеко от Земли. Обозначим радиусы орбит Меркурия, Венеры и Земли через r₁, r₂ и R и определим разность геоцентрических долгот Земли и каждой из двух внутренних планет j₁ и j₂ в данный момент. Для Меркурия получаем

 

 

Разница долгот Земли и Венеры вычисляется из треугольника Солнце-Венера-Земля с учетом свойства смежных углов:

 

 

Время, оставшееся до нижнего соединения внутренней планеты, равно

 

 

где S - синодический период внутренней планеты, равный 115.9 суткам для Меркурия и 583.9 суткам для Венеры. Подставляя численные значения, получаем, что нижнее соединение Меркурия произойдет через 21.6 дня, а нижнее соединение Венеры - через 15.6 дней после рассматриваемого момента. Таким образом, Венера вступит в нижнее соединение на 6 суток раньше Меркурия.

 

 

7. Условие. Два метеорных роя движутся вокруг Солнца в точности по одной и той же орбите, но в разных направлениях. В один момент времени оба роя встречаются друг с другом и с Землей. При этом на Земле наблюдаются два метеорных потока с радиантами, имеющими координаты a=6ч, d=-66.6? и a=18ч, d=0?. Найти эксцентриситет орбиты метеорных роев. В какую дату наблюдались метеорные потоки? Орбиту Земли считать круговой.

 

7. Решение. Так как оба метеорных роя движутся по одной и той же орбите в разные стороны, в момент их встречи они будут иметь гелиоцентрические скорости, равные по величине и противоположные по направлению. Радиант метеорного потока указывает направление, противоположное геоцентрической скорости метеоров, поэтому радианты двух потоков не оказались в противоположных точках неба.

 

 

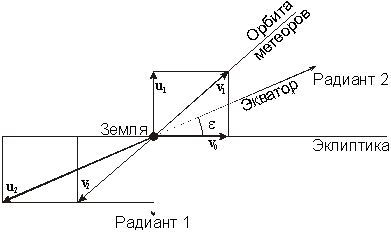
Обозначим вектор скорости Земли через v₀, вектора гелиоцентрических скоростей метеорных потоков через v₁ и v₂, а вектора их геоцентрических скоростей через u₁ и u₂. Для этих векторов справедливы соотношения

u₁ = v₁ - v₀,

u₂ = v₂ - v₀ = - v₁ - v₀.

 

Складывая их, получаем:

u₁ + u₂ = -2v₀.

 

Радиант первого метеорного потока находится в южном полюсе эклиптики, следовательно, плоскость рисунка, содержащая вектор u₁, перпендикулярна плоскости эклиптики, пересекая ее по прямой, содержащей вектор v₀. Оба вектора перпендикулярны радиусу-вектору Земли, направленному из центра Солнца, и вся картинная плоскость, в том числе и гелиоцентрические скорости метеоров, перпендикулярны линии Земля-Солнце. Следовательно, в момент встречи с Землей метеоры находились в точке перигелия или афелия своей орбиты, если эта орбита не круговая.

Точка эклиптики, в направлении которой двигалась Земля в момент встречи с метеорами - одна из двух точек пересечения большого круга эклиптики и большого круга картинной плоскости. Последний представляет собой круг склонения, охватывающий все точки неба с прямым восхождением 6ч и 18ч (в этом можно убедиться по координатам радиантов потоков). Значит, две точки пересечения больших кругов - точки солнцестояний. Из последнего векторного уравнения следует, что проекции векторов u₂ и v₀ на эклиптику имеют противоположные знаки (так как вектор u₁ перпендикулярен эклиптике). С учетом координат второго радианта делаем вывод, что движение Земли направлено в точку солнцестояния, ближайшую к радианту второго потока - в точку зимнего солнцестояния. Такое направление скорости Земля имеет в день весеннего равноденствия - 21 марта. Остается ответить на первый вопрос задачи.

Угол между направлением на второй радиант (небесным экватором) и скоростью движения Земли e равен 23.4?. Спроектировав векторное выражение для суммы скоростей u₁ и u₂ на две координатные оси, получаем:

 

u₁ = u₂ sine,

2v₀ = u₂ cose

 

и далее

u₁ = 2v₀ tge.

 

Гелиоцентрическая скорость метеоров в момент встречи с Землей равна

 

 

Эта скорость превышает круговую скорость v₀, но не превосходит вторую космическую скорость. Таким образом, орбита метеоров эллиптическая, и они находятся в точке перигелия. Обозначив расстояние от Солнца до Земли через r,? запишем выражение для скорости тела в перигелии:

 

 

Здесь a - большая полуось орбиты метеорных тел, e - ее эксцентриситет, M - масса Солнца. В результате,

e=4tg²e=0.75.

 

 

8. Условие. С помощью Гигантского Оптического Космического телескопа со сверхвысоким угловым разрешением астрономы будущего смогли рассмотреть диск звезды Бетельгейзе (a Ориона). У какого объекта поверхностная яркость (яркость единицы угловой площади) больше - у Бетельгейзе или у Венеры? Во сколько раз?

 

8. Решение. Для решения задачи необходимо вспомнить, что при отсутствии поглощения света поверхностная яркость светила не зависит от его расстояния до наблюдателя. Общая яркость уменьшается пропорционально квадрату расстояния, но в той же пропорции уменьшается и видимая площадь светила. Для звезд, самостоятельно излучающих энергию, в приближении абсолютно черного тела поверхностная яркость определяется только температурой поверхности звезды, увеличиваясь пропорционально ее четвертой степени. Бетельгейзе - красный сверхгигант спектрального класса M2 с температурой поверхности около 3000 K, что вдвое меньше солнечной. Поверхностная яркость Бетельгейзе будет в 16 раз меньше поверхностной яркости Солнца.

Венера сама в видимом диапазоне спектра не излучает, а только отражает свет Солнца. Отношение максимальной поверхностной яркости Венеры (в центре диска вблизи верхнего соединения) и поверхностной яркости Солнца будет равно

 

 

Здесь A - альбедо Венеры, r - радиус Солнца и R - радиус орбиты Венеры. В итоге, поверхностная яркость Бетельгейзе в 2330 раз превосходит поверхностную яркость Венеры.

 

 

9. Условие. Шаровое звездное скопление имеет на нашем небе блеск 4.5^m и видимый диаметр 25¢. Расстояние до скопления составляет 3 кпк. Считая, что скопление состоит из звезд, похожих на Солнце, равномерно распределенных по объему внутри шара, оцените освещенность на ночной стороне обитаемой планеты, обращающейся вокруг одной из центральных звезд скопления. Сравните ее с освещенностью в лунную ночь на Земле. Поглощением света в межзвездной среде и в атмосфере планеты пренебречь.

 

9. Решение. Выражая угловой диаметр скопления в радианах, умножая на расстояние до скопления и деля на 2, получаем радиус скопления r₀, равный 10.9 пк. Объем скопления равен

 

 

Солнце имеет абсолютную звездную величину M₀, равную +4.7^m. С расстояния d, равного 3 кпк, оно выглядело бы как звезда величины m₀:

 

 

Обозначив звездную величину всего скопления через m, получаем выражение для количества звезд в скоплении

 

 

и объемной концентрации звезд

 

 

На ночном небе планеты в центре скопления видны звезды одной половины шара, равномерно заполняющие ее по объему. Обозначим освещенность, которую создает на планете в центре скопления одна звезда 0^m через J. Рассчитаем освещенность, которую создадут на этой планете все звезды, попадающие в тонкую полусферическую оболочку с радиусом r и толщиной Dr. Количество этих звезд будет равно произведению концентрации звезд на объем оболочки:

 

 

Звездная величина и освещенность от каждой звезды на планете составит

 

 

Здесь r выражается в парсеках. Освещенность на ночном небе от всех звезд полусферы равна

 

 

Мы видим, что эта освещенность пропорциональна толщине оболочки и не зависит от ее радиуса. Представляя всю полусферу внутри скопления как сложение подобных оболочек, мы получаем выражение для полной освещенности от ночного неба планеты:

 

 

Суммарная звездная величина всех звезд половины шара равна

 

 

Небо этой планеты будет значительно ярче безлунного ночного неба на Земле, и светила вне шарового скопления дадут лишь незначительный вклад в его яркость. Но лунная ночь на Земле (блеск полной Луны равен -12.7^m) все же в 63 раза ярче, чем небо планеты в центре шарового скопления.

 

 

10. Условие. Галактика имеет радиус 15 кпк и значительно меньшую толщину диска. Масса галактики равна 10¹¹ масс Солнца и равномерно распределена по объему галактики. Две звезды обращаются вокруг центра галактики в одном направлении по круговым орбитам с радиусами 5 и 10 кпк. Найти синодический период первой звезды при наблюдении из окрестностей второй звезды.

 

10. Решение. Массовая плотность вещества внутри галактики r равна

 

 

Здесь M, R и d - масса, радиус и толщина диска галактики. В некотором приближении можно считать, что при вращении звезды по круговой орбите с радиусом r внутри диска на нее будет влиять только та часть галактики, которая заключена внутри цилиндра с радиусом r. Масса этой части галактики равна

 

 

Угловая скорость вращения звезды вокруг центра Галактики составит

 

 

Здесь w₀ - угловая скорость вращения края галактики. Обратим внимание, что зависимость угловой скорости от расстояния в данном случае более слабая, чем для кеплеровских орбит, где мы бы получили степень -3/2. Синодический период звезды с радиусом орбиты r₁ при наблюдении со звезды с радиусом орбиты r₂ равен

 

 

Подставляя численные значения, получаем величину синодического периода: 1.07 миллиардов лет.

 

 

 

Версия для печати