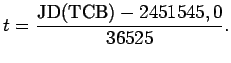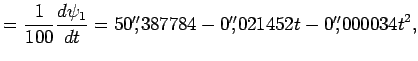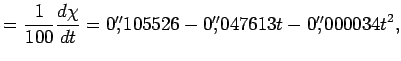7.1. Причины прецессии и нутации
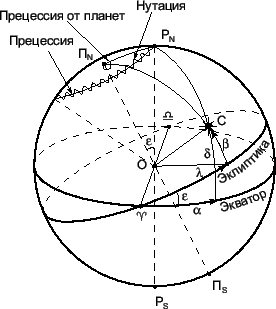
Рассмотрим две системы координат: экваториальную и эклиптическую (рис. 7.1).
Системы координат определяются плоскостями небесного экватора и эклиптики и точкой их пересечения
Положение звезды ![]() относительно этих систем характеризуется
экваториальными и эклиптическими координатами:
относительно этих систем характеризуется
экваториальными и эклиптическими координатами:
![]() и
и
![]() , соответственно. При смещении точек
, соответственно. При смещении точек ![]() и
и
![]() происходит изменение сторон треугольника
происходит изменение сторон треугольника ![]() , то
есть изменение координат звезды. Причиной смещения оси
, то
есть изменение координат звезды. Причиной смещения оси ![]() является лунно-солнечная прецессия, а оси
является лунно-солнечная прецессия, а оси ![]() - прецессия от планет.
- прецессия от планет.
Явление лунно-солнечной прецессии приводит к тому, что точка
весеннего равноденствия перемещается по эклиптике навстречу
Солнцу со скоростью примерно
![]() в год. В результате
прецессионного движений следующее равноденствие наступает раньше,
чем Солнце пройдет
в год. В результате
прецессионного движений следующее равноденствие наступает раньше,
чем Солнце пройдет ![]() по эклиптике. Поэтому другое
название прецессии - предварение
равноденствий. Ясно, что звездный год, или время, требуемое
Солнцу для совершения полного
оборота (или прохождения
по эклиптике. Поэтому другое
название прецессии - предварение
равноденствий. Ясно, что звездный год, или время, требуемое
Солнцу для совершения полного
оборота (или прохождения ![]() ) по эклиптике, будет длиннее
тропического года
(времени между двумя последовательными
прохождениями Солнца через точку весеннего равноденствия) на
) по эклиптике, будет длиннее
тропического года
(времени между двумя последовательными
прохождениями Солнца через точку весеннего равноденствия) на
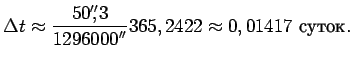
На прецессионное движение оси вращения Земли накладывается
колебательное движение: полюс мира описывает за 18,6 года эллипс
с осями
![]() и
и
![]() относительно среднего положения.
Это движение было названо нутацией. В результате полюс
мира
описывает волнистую линию на небесной сфере (рис. 7.1 и
рис. 1.1).
относительно среднего положения.
Это движение было названо нутацией. В результате полюс
мира
описывает волнистую линию на небесной сфере (рис. 7.1 и
рис. 1.1).
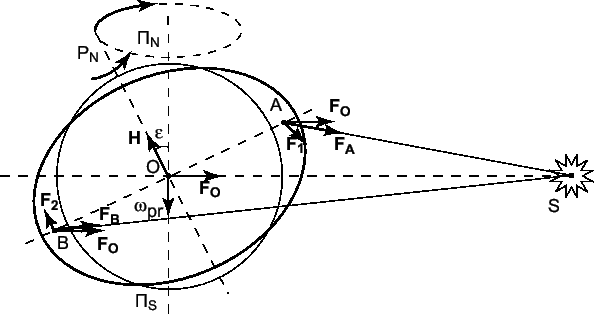
Причиной прецессии и нутации является несферичность Земли и несовпадение плоскостей экватора и эклиптики. В результате гравитационного притяжения Луной и Солнцем экваториального утолщения Земли возникает момент сил, стремящийся совместить плоскости экватора и эклиптики (рис. 7.2).
Как будет показано ниже, лунно-солнечный момент сил, вызывающий прецессию пропорционален
Из рис. 7.2 видно, что так как ![]() , то
, то
![]() и из векторных равенств
и из векторных равенств
![]() ,
,
![]() получим
получим
![]() .
.
Пара сил ![]() и
и ![]() , следовательно, стремится
повернуть плоскость экватора
, следовательно, стремится
повернуть плоскость экватора ![]() по часовой стрелке. Из-за
вращения Земли такого поворота не происходит, но ориентация оси
вращения изменяется: она описывает в пространстве конус, и угол
между осью вращения Земли и осью
по часовой стрелке. Из-за
вращения Земли такого поворота не происходит, но ориентация оси
вращения изменяется: она описывает в пространстве конус, и угол
между осью вращения Земли и осью ![]() равен
равен
![]() .
.
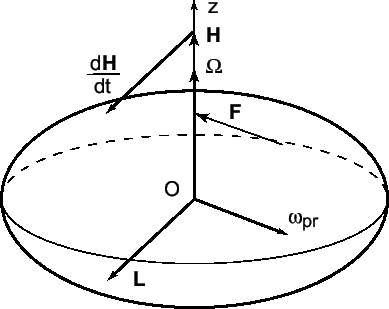
Направление движения оси определим из следующих соображений. Воспользуемся для этого теоремой Резаля, которая, по существу, является интерпретацией теоремы об изменении углового момента тела (7.1):
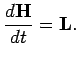
Пусть к телу приложена сила ![]() , как показано на
рис. 7.3.
, как показано на
рис. 7.3.
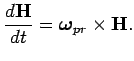
где
Применительно к рис. 7.2 вектор ![]() направлен
перпендикулярно плоскости листа в сторону от читателя,
следовательно, вектор
направлен
перпендикулярно плоскости листа в сторону от читателя,
следовательно, вектор
![]() направлен в точку
южного полюса эклиптики
направлен в точку
южного полюса эклиптики ![]() ; угол
; угол ![]() равен
равен
![]() ,
,
![]() . Это означает, что
прецессионное движение оси
. Это означает, что
прецессионное движение оси ![]() происходит по часовой стрелке,
если смотреть с северного полюса эклиптики. Рис. 7.2
отражает расположение Земли и Солнца вблизи момента зимнего
солнцестояния: в северном полушарии - зима, в южном - лето.
Нетрудно проверить, что для летнего солнцестояния (Солнце будет
располагаться на рис. 7.2 слева от Земли) момент сил
будет направлен в ту же сторону: перпендикулярно плоскости листа
от читателя. В моменты солнцестояний момент сил, действующий на
экваториальное утолщение Земли максимален; следовательно, угловая
скорость прецессии максимальна. Во время равноденствий момент сил
равен нулю; значит, скорость прецессии равна нулю.
происходит по часовой стрелке,
если смотреть с северного полюса эклиптики. Рис. 7.2
отражает расположение Земли и Солнца вблизи момента зимнего
солнцестояния: в северном полушарии - зима, в южном - лето.
Нетрудно проверить, что для летнего солнцестояния (Солнце будет
располагаться на рис. 7.2 слева от Земли) момент сил
будет направлен в ту же сторону: перпендикулярно плоскости листа
от читателя. В моменты солнцестояний момент сил, действующий на
экваториальное утолщение Земли максимален; следовательно, угловая
скорость прецессии максимальна. Во время равноденствий момент сил
равен нулю; значит, скорость прецессии равна нулю.
В действительности мгновенная угловая скорость прецессии
складывается из двух частей: первая обусловлена моментом сил
притяжения Солнца, вторая - Луны. В результате этого суммарного
эффекта северный полюс мира описывает на небесной сфере кривую,
близкую к окружности, с угловым радиусом
![]() . Период оборота равняется
. Период оборота равняется
![]() лет.
лет.
Изменение расстояния между Землей и Солнцем, Землей и Луной,
наклон орбиты Луны к эклиптике приводят к изменению сил,
действующих на экваториальное утолщение Земли. В результате
величина угла между осями ![]() и
и ![]() меняется: появляются
вариации
меняется: появляются
вариации
![]() с периодами, равными 18,6 лет, 9,3 года, 1
и 0,5 года, 13,7 суток и т.д. Это
- нутационное движение оси вращения Земли.
с периодами, равными 18,6 лет, 9,3 года, 1
и 0,5 года, 13,7 суток и т.д. Это
- нутационное движение оси вращения Земли.
Притяжение планетами экваториального утолщения Земли также должно вызывать прецессионно-нутационное движение оси мира. Однако из-за большого расстояния и малой по сравнению с Солнцем массы влияние планет мало. Максимальные по амплитуде нутационные гармоники не превышают 0,25 мс дуги. В теории нутации МАС 1980 г. этот эффект не учитывался. В новых, более точных теориях, планетная нутация обязательно учитывается.
Гораздо большее влияние планеты оказывают на положение плоскости
эклиптики в пространстве. По определению плоскость эклиптики есть
средняя плоскость земной орбиты. Влияние планет проявляется в
возмущении орбиты Земли; в результате полюс эклиптики смещается
примерно на
![]() в год (рис. 7.1). Смещение полюса
эклиптики (прецессия от планет) приводит к дополнительному
движению точки весеннего равноденствия навстречу Солнцу на
в год (рис. 7.1). Смещение полюса
эклиптики (прецессия от планет) приводит к дополнительному
движению точки весеннего равноденствия навстречу Солнцу на
![]() в столетие и уменьшению наклона эклиптики к экватору в
настоящее время на
в столетие и уменьшению наклона эклиптики к экватору в
настоящее время на
![]() в столетие.
в столетие.
Таким образом лунно-солнечная прецессия приводит к повороту
плоскости экватора Земли и, следовательно, небесного экватора
относительно эклиптики. Прецессия от планет приводит к изменению
положения эклиптики в пространстве (рис. 7.4). На
рис. 7.4 изображены положения эклиптики и экватора на две
эпохи ![]() и
и ![]() .
.
По определению системы координат, задающие плоскости эклиптики и
небесного экватора, являются средними системами координат,
а точки весеннего равноденствия
![]() называются средними. Термин "средняя система
координат",
используемый в астрометрии, подразумевает, что изменение
положения осей систем координат относительно инерциальной системы
координат при преобразовании от одной эпохи к другой происходит
только из-за прецессии. Если учитывается нутация, то система
координат называется истинной.
называются средними. Термин "средняя система
координат",
используемый в астрометрии, подразумевает, что изменение
положения осей систем координат относительно инерциальной системы
координат при преобразовании от одной эпохи к другой происходит
только из-за прецессии. Если учитывается нутация, то система
координат называется истинной.
Положение экваториальной системы относительно эклиптической
системы может быть задано тремя углами Эйлера:
![]() . Угол
. Угол ![]() равен дуге
эклиптики
равен дуге
эклиптики
![]() и называется лунно-солнечной
прецессией за промежуток времени
и называется лунно-солнечной
прецессией за промежуток времени ![]() . В результате
лунно-солнечной прецессии средняя мгновенная точка весеннего
равноденствия
. В результате
лунно-солнечной прецессии средняя мгновенная точка весеннего
равноденствия ![]() смещается на запад по эклиптике
из-за прецессионного движения экватора. Угол
смещается на запад по эклиптике
из-за прецессионного движения экватора. Угол ![]() равен
дуге
равен
дуге
![]() среднего мгновенного экватора
среднего мгновенного экватора ![]() и
называется прецессией от планет. В
результате прецессии от планет средняя мгновенная точка весеннего
равноденствия
и
называется прецессией от планет. В
результате прецессии от планет средняя мгновенная точка весеннего
равноденствия
![]() смещается вдоль среднего мгновенного
экватора. Наклон мгновенной эклиптики
смещается вдоль среднего мгновенного
экватора. Наклон мгновенной эклиптики ![]() к экватору
к экватору ![]() равен
равен
![]() , а эклиптики
, а эклиптики ![]() на начальную эпоху к экватору
на начальную эпоху к экватору
![]() равен
равен
![]() . Если, согласно Ньюкомбу, обозначить
через
. Если, согласно Ньюкомбу, обозначить
через ![]() промежуток времени в юлианских столетиях от эпохи
1900.0, то прецессионные параметры
промежуток времени в юлианских столетиях от эпохи
1900.0, то прецессионные параметры
![]() определяются следующими разложениями:
определяются следующими разложениями:
При
В соответствии с решением МАС (1976 г.), принявшим новые значения
астрономических постоянных, коэффициенты разложений прецессионных
параметров Ньюкомба были перевычислены. Если начальная эпоха
![]() совпадает с фундаментальной эпохой J2000.0, то разложения
имеют следующий вид:
совпадает с фундаментальной эпохой J2000.0, то разложения
имеют следующий вид:
где
Наклон эклиптики к экватору на эпоху J2000.0 равен
Годичные скорости лунно-солнечной прецессии и прецессии от планет найдем, продифференцировав уравнения (7.5) и (7.6) и уменьшив результат в 100 раз. Тогда
Величины
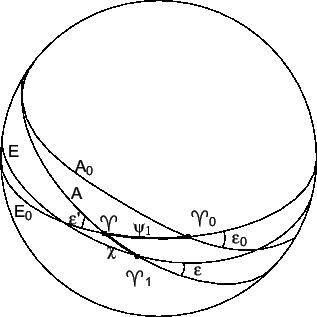
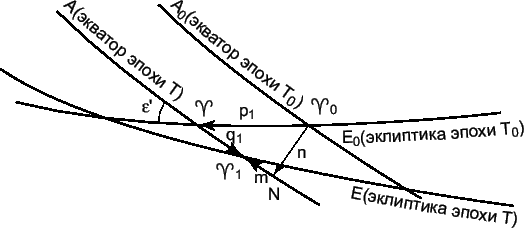
Обратимся теперь к рис. 7.5, на котором изображено
годичное смещение в пространстве плоскостей экватора и эклиптики.
Проведем круг склонений через точку ![]() и его пересечение
с экватором
и его пересечение
с экватором ![]() обозначим как
обозначим как ![]() .
.
|
Рис. 7.5. Прецессия по прямому восхождению и склонению, лунно-солнечная прецессия и прецессия от планет. |
Из-за малости прецессионных постоянных ![]() получим из
треугольника
получим из
треугольника
![]() , который можно считать плоским,
соотношения между
, который можно считать плоским,
соотношения между ![]() и
и ![]() :
:
Величины
Если исключить из постоянной лунно-солнечной прецессии вклад
планетной прецессии, то получим годичную величину
прецессии по долготе ![]() :
:
Принятое значение постоянной прецессии по долготе для эпохи J2000.0 равно
<< 7. Прецессия и нутация | Оглавление | 7.2. Определение матрицы прецессии >>
|
Публикации с ключевыми словами:
астрометрия - сферическая астрономия - системы координат - шкалы времени
Публикации со словами: астрометрия - сферическая астрономия - системы координат - шкалы времени | |
См. также:
Все публикации на ту же тему >> | |