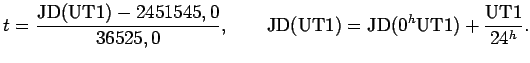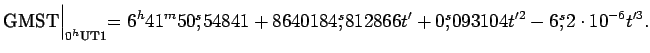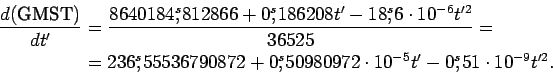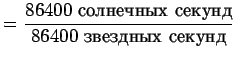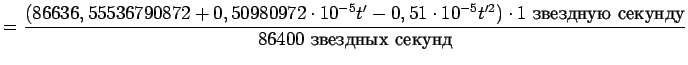Астронет | Картинка дня | Обзоры astro-ph | Новости | Статьи | Книги | Карта неба | Созвездия | Переменные Звезды | Глоссарий

Физика космоса | Биографии | Словарь | Ключевые слова | Астрономия в России | Форумы | Семинары | Сверхновые

<< 5.8. Летосчисление | Оглавление | 6. Эффекты, искажающие положение >>

5.9. Связь всемирного и звездного времени

Рассмотрим теперь вопрос о связи всемирного и звездного времени.

Всемирное и звездное время определяются вращением Земли относительно Солнца и относительно точки весеннего равноденствия, соответственно. Следовательно, в уравнение связи входят параметры движения Солнца по небесной сфере. Если эти параметры известны точно, то можно найти точное уравнение, которое связывает всемирное и звездное время.

И всемирная, и звездная шкалы времени неравномерны относительно атомной шкалы из-за вариаций скорости вращения Земли. Так как атомная шкала времени совершенно не зависит от вращения Земли, то связь TAI с UT может быть определена только эмпирически, по наблюдениям звезд или радиоисточников. Причины, которые приводят к изменению скорости вращения Земли, до конца не известны, и, поэтому, невозможно построить точную теорию вращения Земли. Это означает, что для определения разницы необходимы регулярные наблюдения. С этой точки зрения современные астрометристы находятся в том же положении, что древние астрономы: для определения времени необходимы непрерывные наблюдения.

В данном параграфе мы получим формулы, связывающие всемирное и звездное время. Описание методов наблюдений, целью которых является определение разницы , не входит в задачи курса. Однако при описании основ редукции РСДБ наблюдений эта тема будет затронута.

По определению звездное время на меридиане Гринвича GST равно часовому углу точки весеннего равноденствия относительно Гринвича:

В уравнении (5.76) точка всегда относится к равноденствию даты, но нутация может учитываться или нет. Если предполагается, что нутация учитывается, то есть наблюдения относятся к истинному равноденствию , то звездное время называется истинным. Если точка обозначает среднее равноденствие, то уравнение (5.76) определяет среднее звездное время. Обычно его обозначают как GMST (Greenwich Mean Sidereal Time), тогда как истинное время как GAST (Greenwich Apparent Sidereal Time).

Разность между двумя звездными временами называется уравнением равноденствий (по-английски "equation of the equinoxes" или кратко "eq eq"). Ниже будет показано (в главе 7) как можно получить уравнение равноденствий. Пока запишем, что

Для вывода уравнения связи всемирного и звездного времени используем определение тропического года. Для любого светила (в том числе и Солнца) справедливо уравнение (5.15). Запишем его относительно гринвичского меридиана для среднего экваториального Солнца:

Еще раз подчеркнем, что - прямое восхождение среднего экваториального Солнца, отсчитываемое от среднего равноденствия. Используя (5.3), получим:

В течение тропического года прямое восхождение среднего экваториального Солнца увеличивается ровно на . За сутки прямое восхождение увеличивается на . Значит, если - прямое восхождение среднего экваториального Солнца на начальную эпоху, то

где , - продолжительность тропического года в средних солнечных сутках.

Из уравнения (5.77) получим:

Это и есть точное уравнение, связывающее среднее гринвичское звездное время со средним солнечным. Предполагается, что в (5.78) возрастает равномерно с UT. Это естественно, так как это и есть определение среднего солнечного времени.

Концепция среднего экваториального Солнца была введена С.Ньюкомбом в 1895 г., когда измерить неравномерность вращения Земли еще было нельзя. Ньюкомб, поэтому, не делал различия между всемирным и эфемеридным средним Солнцем. Фиктивная точка, связанная с Солнцем, которую он изучал, двигалась равномерно (если не принимать во внимание малых вековых эффектов) и в звездном, и в динамическом времени. Он эмпирически получил выражения для прямого восхождения среднего экваториального Солнца. Недавно (в 1982 г.) коэффициенты формулы С.Ньюкомба были изменены из-за ревизии астрономических констант (система МАС 1976):

где - число юлианских столетий от момента наблюдений в UT1 до эпохи J2000.0:

Перепишем выражение для  (5.81) следующим образом:

, - количество целых суток от фундаментальной эпохи J2000.0.

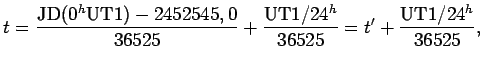
Тогда, используя (5.77), получим:

Из (5.82) найдем изменение среднего звездного времени за средние солнечные сутки:

Очевидно, что изменение звездного времени за одни средние солнечные сутки равно ежесуточному увеличению прямого восхождения среднего Солнца. Если, например, 21 марта среднее Солнце и точка весеннего равноденствия кульминировали на каком-либо меридиане одновременно, то за средние сутки Солнце сместится относительно звезд навстречу суточному вращению небесной сферы, т.е. к востоку, и будет кульминировать позднее точки весеннего равноденствия. Чтобы произошла кульминация среднего Солнца, Земля должна совершить дополнительный поворот. 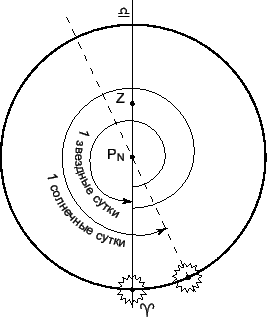Этот поворот совершается за в звездном времени; иначе говоря, средние солнечные сутки, выраженные в звездном времени, на длиннее звездных (рис. 5.17).

С учетом (5.83) получим:

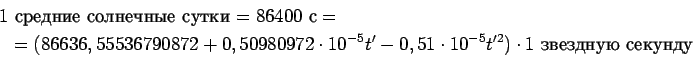Отношение продолжительностей средних солнечных и средних звездных суток равно:

Пусть . Используя выражения (5.82),(5.84), перепишем (5.79) в рекомендуемом Международной службой вращения Земли виде:

Из выражения (5.85) следует, что среднее звездное гринвичское время, как и всемирное UT1, не может быть определено на основе теории. Поэтому часто при невысокой точности редукции наблюдений пренебрегают разностью . В этом случае GMST является функцией только атомного времени UTC. При редукции с высокой точностью (например, РСДБ наблюдений) приходится использовать публикуемые МСВЗ значения и интерполировать или экстраполировать их на момент наблюдения.

Для быстрых приближенных вычислений среднего гринвичского звездного времени с использованием "Астрономического Ежегодника" перепишем выражение (5.85) в следующем виде:

где . Всемирное время UT1 может быть найдено из поясного или декретного, пренебрегая разностью . Необходимо, конечно же, учитывать введено в данный момент летнее время или нет.

Если требуемая точность вычислений невысокая, то можно использовать значения из "Астрономического Ежегодника" (таблица IIа или IIIa). Значения (среднее гринвичское время на ) приводятся на стр.6-9.

После того, как найдено гринвичское время GMST, местное звездное время на долготе получается по формуле (5.13): .

Из (5.86) легко получить обратную зависимость: переход от звездного времени к солнечному

Здесь использовано разложение в ряд Тейлора по малому параметру

где

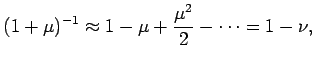
В заключение главы для усвоения метода перевода всемирного в звездное время решим задачу, используя "Астрономический Ежегодник" 2000 г.: найти среднее звездное время, соответствующее моменту московского времени для точки с долготой 10 мая 2000 г.

Так как и 10 мая используется летнее время, то . Среднее гринвичское время на всемирного времени 10 мая 2000 г. выписываем из "Астрономического Ежегодника" (с.6). Имеем:

Вычисление поправок производится при помощи табл. IIIа "Астрономического Ежегодника" (с.622).

---

<< 5.8. Летосчисление | Оглавление | 6. Эффекты, искажающие положение >>

Публикации с ключевыми словами: астрометрия - сферическая астрономия - системы координат - шкалы времени Публикации со словами: астрометрия - сферическая астрономия - системы координат - шкалы времени
См. также: 80 лет со дня рождения Альберта Петровича Гуляева Руководство по практической работе с каталогом Hipparcos К 70-летию Вилена Валентиновича Нестерова Полная версия "Сферической астрономии" В.Е.Жарова Обзор геостационарной орбиты на двойном астрографе УАФО Отдел пульсарной астрометрии ПРАО АКЦ ФИАН Прямое определение расстояния до центра Галактики Все публикации на ту же тему >>