Движущиеся группы звезд: до и после HIPPARCOS
<< 2. Проблемы терминологии | Оглавление | 4. Движущиеся группы >>
- 3.1 Метод радиантов
- 3.2 Метод Ратнатунги
- 3.3 Метод главных звезд
- 3.4 Кластерный анализ
- 3.5 Метод "бегущего" куба (шара)
- 3.6 Непараметрические оценки плотности
- 3.7 Вэйвлет-анализ
- 3.8 Метод "спагетти"
3. Как искать движущиеся группы?
Методы выделения группировок звезд, которые обладают общим движением в пространстве, можно разделить на три типа в зависимости от тех наблюдательных данных, которые используются:
- методы, в которых используется только информация о положениях звезд на небе и их собственных движениях с возможным привлечением данных о лучевых скоростях;
- методы, в которых также используются параллаксы звезд;
- методы, основанные на данных о пространственных скоростях.
Рассмотрим более подробно несколько методов поиска движущихся скоплений.
3.1 Метод радиантов
Для определения радиантов и антирадиантов возможных движущихся групп рассматривается совокупность векторов собственных движений звезд. Точки сходимости собственных движений приближенно определяются графически. Затем положения этих точек можно уточнить, например, минимизируя сумму квадратов расстояний от точки предполагаемого радианта до больших кругов, проведенных вдоль векторов собственных движений звезд.
В методе радиантов возникает проблема отбора членов группы. Часто в качестве таковых берут звезды, для которых выполняется неравенство
 |
(1) |
где 
- позиционный угол вектора собственного
движения звезды;
- позиционный угол направления
со звезды на радиант; 
- угловое расстояние между
звездой и радиантом; 
- параметр.
Заметим, что метод радиантов имеет элементы субъективизма,
связанные с предварительным выбором радианта и параметра .
Для отбора членов группы можно привлечь также информацию о лучевых скоростях звезд.
3.2 Метод Ратнатунги
В этом методе [6] используется информация о лучевых скоростях звезд и позиционных углах векторов собственных движений. Автор переходит от этих параметров к двум параметрам, которые равны нулю для членов движущейся группы, а именно лучевая скорость исправляется за движение группы относительно Солнца, а позиционный угол собственного движения приводится в систему отсчета, в которой полюса совпадают с точками радианта и антирадианта. При этом вводится множитель, равный синусу углового расстояния между звездой и апексом (антирадиантом) группы.
Заметим, что для применения метода Ратнатунги необходима
предварительная информация о движении группы. Этот
метод можно использовать для оценки степени компактности
движущейся группы в пространстве скоростей.
3.3 Метод главных звезд
В этом методе [7,8] используются данные о пространственных скоростях звезд. В пространстве скоростей выделяются звезды - центры сгущений, вокруг которых имеются локальные максимумы плотности. Для этого вокруг каждой звезды строится сфера определенного радиуса и подсчитывается число звезд-спутников, оказавшихся внутри этой сферы. Находятся звезды, которые имеют максимальное число спутников по сравнению с их спутниками. Эти звезды - центры локальных сгущений - будем называть главными звездами.
Одна из проблем этого метода - выбор радиуса сферы. Слишком
большое значение радиуса уменьшает разрешение метода, слишком
малый радиус не позволяет выделять группы из-за ошибок наблюдений
и реальной дисперсии скоростей в группе звезд. Разумный компромисс
км/с.
3.4 Кластерный анализ
Методы кластерного анализа используются во многих областях науки для поиска сгущений объектов. Идея этого подхода состоит в представлении распределения звезд в пространстве скоростей в виде иерархического дерева (см., например, [8,9]).
Листья дерева - отдельные звезды. Листья объединяются в ветви-кластеры по определенному закону максимальной близости. Затем каждый кластер, состоящий из двух и более звезд, рассматривается как отдельный объект, и процедура кластеризации повторяется снова.
Проблемы кластерного анализа - выбор расстояния между объектами и выбор момента "обрезания" в процедуре кластеризации.
3.5 Метод "бегущего" куба (шара)
Этот метод состоит в сканировании пространства скоростей кубом или шаром небольшого объема. Подсчитывается число звезд в пределах этого куба или шара. Полученное число сравнивается с числом звезд, ожидаемым при случайном распределении. Если наблюдаемое число значимо превосходит ожидаемое, то можно предположить, что в этом кубе или шаре располагается движущаяся группа или часть группы.
Проблему составляет выбор размера куба или шара, а также возможность объединения нескольких соседних кубов или шаров с повышенной концентрацией звезд в одну группу.
3.6 Непараметрические оценки плотности
При таком подходе
[10-11]
распределение остаточных скоростей
звезд в точке
оценивается с помощью "ядерной"
функции вида
 |
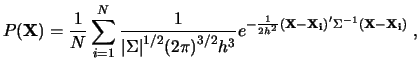(2) |
где 
- число звезд в рассматриваемой выборке;
- вектор
пространственной скорости 
-й звезды; 
- параметр
сглаживания (или ширина окна); 
- ковариационная
матрица.
Предполагается, что функция
 |
(3) |
где первое слагаемое определяет вклад звезд поля, а второе - вклад звезд группы. Для звезд поля можно предположить эллипсоидальное распределение, параметры которого (средние и элементы ковариационной матрицы) определяются из наблюдений.
Члены групп выделяются по превышению функцией (2) некоторого порогового
значения 
, которое зависит от принятого уровня значимости.
Процедура формирования групп заканчивается, если больше не находится
новых членов.
3.7 Вэйвлет-анализ
Преобразование "маленькой волны", или вэйвлет-анализ, в последнее десятилетие нашел широкое применение практически во всех областях естествознания, где требуется выделить те или иные структуры.
При исследовании пространства скоростей звезд применяется
трехмерный вэйвлет-анализ [12,13]. Если мы рассмотрим
распределение звезд в пространстве скоростей как трехмерный сигнал
, то мы можем представить преобразование
"маленькой волны" как свертку этого распределения с некоторой
функцией
. Эта функция выбирается таким
образом, чтобы она достаточно быстро спадала при удалении от
интересующей нас точки. Коэффициенты вэйвлета имеют большие
положительные величины в областях повышенной плотности и большие
по модулю, но отрицательные значения - в местах пониженной
плотности звезд.
Для того чтобы отделить вероятно неслучайные сгущения звезд от случайных флуктуаций, необходимо ввести некоторые пороговые значения вэйвлет-коэффициентов, которые в общем случае зависят от масштаба и положения точки в пространстве скоростей. Пороговые значения определяются из оценок уровня шума, порожденного при том же самом масштабе равномерно случайным сигналом. Причем крупномасштабные характеристики случайного сигнала совпадают с так называемыми гросс-характеристиками наблюдаемого распределения.
3.8 Метод "спагетти"
В этом методе [14] используется только астрометрическая информация: положения звезд на небе, их параллаксы и собственные движения. Каждой звезде ставится в соответствие некоторый цилиндр ("макаронина") в пространстве скоростей. Этот цилиндр ортогонален вектору тангенциальной скорости звезды и параллелен лучу зрения. Толщина цилиндра определяется ошибками собственного движения и параллакса звезды.
Спагетти, соответствующие звездам одного и того же движущегося скопления, пересекаются в одной и той же точке - центроиде скопления.
Таким образом, выделяя сгущения этих точек в пространстве скоростей, мы находим вероятные центроиды движущихся групп звезд.
<< 2. Проблемы терминологии | Оглавление | 4. Движущиеся группы >>
|
Публикации с ключевыми словами:
группы звезд - Собственное движение - астрометрия - ИСЗ Гипархос - Hipparcos
Публикации со словами: группы звезд - Собственное движение - астрометрия - ИСЗ Гипархос - Hipparcos | |
См. также:
Все публикации на ту же тему >> | |
